




Step-by-Step Guide: Multiplying Numbers by 10, 100, and 1000
Mathematical multiplication by 10s, 100s, and 1000s is a significant topic. It is utilized in a number of mathematical operations, including multiplication, division, and percentage. There are two alternative ways to accomplish it. The long method and the short method. The short method is easier to do, but it takes more time. The long method takes less time, but it's harder to do than the short method.
The process of multiplying by 10, 100 multiplication and 1000 involves finding the product of the first number multiplied by 10, then the next number multiplied by 100, and then the last number multiplied by 1000.
In this topic, we will mainly discuss things related to multiplication by 10, 100 and 1000. Apart from this, in this topic, we will also look at worksheets and examples related to them, which will help us better understand this topic.
Multiplication Chart with One to Hundred Table
Here one to hundred tables are given, which help to improve this topic:
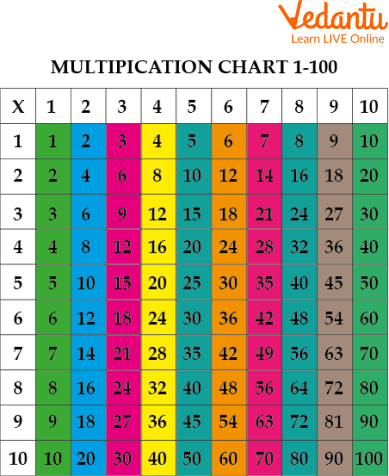
Multiplication Chart
Multiplication Table of 10
Here are the multiplication tables of 10, which are like this
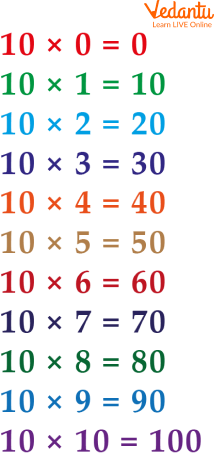
Table of 10
Multiplication Table of 100
Here are the multiplication tables of 100, which are like this

Table of 100
Multiplication Table of 1000
Here are the multiplication tables of 1000, which are like this

Table of 1000
The result of a multiplication by 100 is the integer with two zeros to its right. The result of a multiplication by 1000 is the number with three zeros to the right of the original integer. The result of a 10x calculation is the number with 1 zero to the right of the original.
Multiply by 10, 100 and 1000 Example
Here is an example for multiplying 10 by 100 and 1000, which is as follows:
Example: Multiply 1.3 with 10
Ans: Here, as per the question, we must multiply 1.3 by 10.
So, when a whole number is multiplied by ten, the multiplicand is followed by one zero.
So on multiplying a decimal by 10, we shift the decimal point to the right by one place, i.e. $1.3 \times 10 = 13.0$
Example- Multiply 3.62 with 100
Ans: Here, as per the question, we must multiply 3.62 by 100.
So as we know, when a whole number is multiplied by 100, the multiplicand is followed by two zeros.
So on multiplying a decimal by 100, we shift the decimal point to the right by two places i.e. $3.62 \times 100 = 3.6200 = 362$
Example- Multiply 56.3 with 1000
Ans: Here, as per the question, we must multiply 5.63 by 1000.
So as we know, when a whole number is multiplied by 1000, the multiplicand is followed by three zeros.
So on multiplying a decimal by 1000, we shift the decimal point to the right by three places i.e. $56.3 \times 1000 = 5.63000 = 563.0$
Multiply by 10, 100 and 1000 Worksheet
Here is a worksheet for multiplying 10 by 100 and 1000, which is as follows:
Q 1. Multiply 47 × 10
Ans: 470
Q 2. Multiply 57.25 × 100
Ans: 5725
Q 3. Multiply 125.056 × 1000
Ans: 125,056
Q 4. Multiply 29 × 100
Ans: 2900
Q 5. Multiply 25.63 × 10
Ans: 2,563
Summary
The significance of multiplication by 10s, 100s, and 1000s in math was covered in this article. Multiplication by 10, 100 and 1000 is important because it is a way to represent large numbers in a more manageable form. It is also an important concept to learn because it can be used in many other areas of mathematics. In conclusion, the 10, 100, and 1000 multiplication methods are very simple and easy to use. They can be used to find the product of two numbers.
FAQs on Multiplication by 10, 100 and 1000 Made Easy
1. What is the simplest rule for multiplying any whole number by 10, 100, or 1000?
The simplest rule is to add zeros to the end of the number. The number of zeros you add is the same as the number of zeros in the multiplier.
- To multiply by 10, add one zero to the end of the number (e.g., 58 x 10 = 580).
- To multiply by 100, add two zeros to the end of the number (e.g., 58 x 100 = 5800).
- To multiply by 1000, add three zeros to the end of the number (e.g., 58 x 1000 = 58000).
2. How is multiplying a number by 10 different from multiplying it by 100?
The key difference is the change in place value. When you multiply a number by 10, each digit shifts one place to the left, making the number ten times bigger. When you multiply by 100, each digit shifts two places to the left, making the number one hundred times bigger. For example, 45 x 10 = 450, but 45 x 100 = 4500.
3. Why does adding a zero to a whole number work as a shortcut for multiplying by 10?
Adding a zero is a shortcut because our number system is based on tens (base-10). When you add a zero to the end of a whole number, you are essentially pushing every digit one place to the left into a higher place value. The 'ones' digit moves to the 'tens' place, the 'tens' to the 'hundreds', and so on. This action makes the total value of the number ten times greater, which is exactly what multiplying by 10 does.
4. What is the method for multiplying a decimal number by 10, 100, or 1000?
For decimal numbers, instead of adding zeros, you move the decimal point to the right. The number of places you move it is equal to the number of zeros in the multiplier.
- To multiply by 10, move the decimal point one place to the right (e.g., 6.281 x 10 = 62.81).
- To multiply by 100, move the decimal point two places to the right (e.g., 6.281 x 100 = 628.1).
- To multiply by 1000, move the decimal point three places to the right (e.g., 6.281 x 1000 = 6281).
5. Can you provide a real-world example of multiplying by 100 or 1000?
Certainly. A common real-world example is converting units of measurement. To convert metres to centimetres, you multiply by 100. So, a rope that is 12 metres long is 12 x 100 = 1200 centimetres long. Similarly, to convert kilograms to grams, you multiply by 1000. A 2-kilogram bag of sugar is 2 x 1000 = 2000 grams.
6. What is the connection between multiplying by 100 and multiplying by 10 twice?
The connection is that they produce the exact same result because 100 is equal to 10 x 10. Therefore, multiplying a number by 100 is the same as multiplying it by 10, and then multiplying the result by 10 again. For example, 15 x 100 is 1500. Alternatively, you can do it in two steps: 15 x 10 = 150, and then 150 x 10 = 1500.
7. What happens if you multiply zero by 10, 100, or 1000? Does the rule change?
The rule does not change, but the result is always zero. This is due to the Zero Property of Multiplication, which states that any number multiplied by zero equals zero. So, 0 x 10 = 0, 0 x 100 = 0, and 0 x 1000 = 0. The shortcut of adding zeros (e.g., 00) still results in a value of zero.
8. Is multiplying a number by 1000 the same as multiplying it by 10 and then by 100? Explain with an example.
Yes, it is exactly the same. This works because 1000 is the same as 10 x 100. The order in which you multiply numbers does not change the final answer (this is the associative property of multiplication).
For example, let's take the number 7:
- Directly: 7 x 1000 = 7000.
- In steps: (7 x 10) x 100 = 70 x 100 = 7000.























