Median of a Triangle

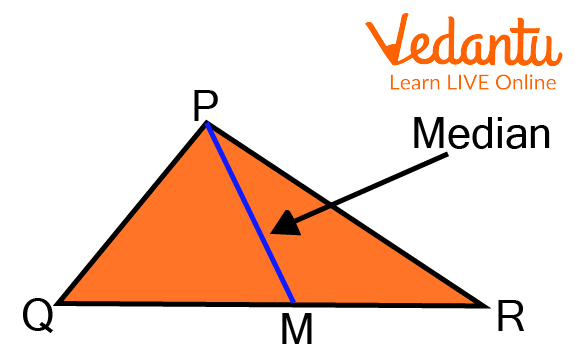
A line segment joining a triangle vertex to the middle of the other side, bisecting that side, is referred to as the median of a triangle in geometry. There are three medians in every triangle, one from each vertex.

At the centroid of the triangle, these medians cross. The median of a triangle is a line segment that connects a vertex to the midpoint of the side that is opposite to that vertex. The median (AD) in the example below divides BC into two equal portions, resulting in BD = DC. This answers, what is a median in geometry?

Median of a Triangle

Properties of Median of a Triangle

A few properties of median of a triangle are listed below:

• A line segment from a triangle's vertex to the middle of its opposite side is said to be the triangle's median.

• It divides the opposing side into two equal portions by cutting it in half.

• A triangle is further divided into two triangles with the same area by its median.

• Any triangle's three medians meet at a single point, regardless of its size or shape.

• Three medians, one from each vertex, exist for each triangle. The triangle's centroid is formed by the intersection of three medians.

• The centroid is the point of concurrency of medians of the triangle.

The Altitude of a Triangle

A line segment making a straight angle (90°) from a triangle's vertex to its opposite side is considered the triangle's altitude. Depending on the type of triangle, an altitude may be inside or outside the triangle. Each triangle has three altitudes, one from each vertex, which all come together at the triangle's orthocenter.

How to Find the Median of a Triangle

The median formula geometry is given as follows.

The first median of a triangle formula is calculated using the median of a triangle theorem, where the triangle's median is $m_{a}$, its sides are $\mathrm{a}, \mathrm{b}$, and $\mathrm{c}$, and the median is established on the side ' $a$ '.

$m_{a}=\sqrt{\dfrac{2 b^{2}+2 c^{2}-a^{2}}{4}}$

The second median of a triangle is calculated using the median of a triangle theorem, where the triangle's median is $m_{b}$, its sides are a, b, and $c$, and the median is established on the side ' $b$ '.

$m_{h}=\sqrt{\dfrac{2 a^{2}+2 c^{2}-b^{2}}{4}}$

The third median of a triangle is calculated using the following formula, where the triangle's median is $m_{c}$, its sides are $\mathrm{a}, \mathrm{b}$, and $\mathrm{c}$, and the median is established on side ' $c$ '.

$m_{c}=\sqrt{\dfrac{2 a^{2}+2 b^{2}-c^{2}}{4}}$

Solved Examples

Q1. Calculate the length of the median of the triangle PQR, whose sides are PQ = 3, PR = 4, and QR = 5 units. The median created on the side QR is given as PM.

Example to Find the Median

Ans: Here, we have to find a PM. So, we have to use the median of the triangle formula i.e.

$P M=\sqrt{\dfrac{2 P Q^{2}+2 P R^{2}-Q R^{2}}{4}}$

$P M=\sqrt{\dfrac{2(3)^{2}+2(4)^{2}-(5)^{2}}{4}}$

where $P Q=3, P R=4, Q R=5$

$PM=\sqrt{\dfrac{18+32-25}{4}}=\sqrt{\dfrac{50-25}{4}}=\sqrt{\dfrac{25}{4}}=\dfrac{5}{2}=2.5 \text { units. }$

Q2. Determine the length of the median of the triangle ABC, whose sides are given as AB = 10, BC = 8, and AC = 13 units, respectively. The median created on side BC is given as AD where D is the median.

Ans: Here, we have to find AD. So, we have to use the median of the triangle formula i.e.

$A D=\sqrt{\dfrac{2 A B^{2}+2 A C^{2}-B C^{2}}{4}}$

$A D=\sqrt{\dfrac{2(10)^{2}+2(13)^{2}-(8)^{2}}{4}}$

where $A B=10, B C=8, A C=13$

$A D=\sqrt{\dfrac{200+338-64}{4}}=\sqrt{\dfrac{474}{4}}=10.88$ units.

Q3. Triangles have a 28 cm, 45 cm, and 53 cm median. What is the triangle's area?

Ans: We have given the Pythagoras triplet i.e. 28cm, 45cm, 53cm.

Thus, the area of a triangle is equal to $\dfrac{4}{3}$ which is multiplied by the area of the triangle formed by the median.

The area of a triangle is $\dfrac{4}{3} \times \dfrac{1}{2} \times 28 \times 45=840 \mathrm{~cm}^{2}$.

Q4. For the given triangle ABC, G is the centroid and BC = 10 units. Determine the length of BD.

Ans: Given,

$\angle \mathrm{GDC}=90$

$\Rightarrow \mathrm{GD}=18 \times \dfrac{1}{3}=6$

$\Rightarrow \mathrm{BG}=15 \times \dfrac{2}{3}=10$

In BGD,

Using Pythagoras theorem,

$\Rightarrow B G^{2}=G D^{2}+B D^{2}$

$\Rightarrow B D^{2}=100-36=64$

$\Rightarrow B D=8$

$\Rightarrow B C=2 B D=2 \times 8=16$

Area of $\Delta \mathrm{BGD}=\dfrac{1}{2} \times \mathrm{GD} \times \mathrm{BD}$

$=\dfrac{1}{2} \times 8 \times 6=24$ sq.units.

Q5. Two equilateral triangles of side 4 cm each but labelled as △ABC and △LHN are not congruent. True or False?

Ans: Two equilateral triangles with equal sides are always congruent no matter how they are labelled. So the statement is False.

Practice Questions

Q1. Write the formula for the median of a triangle if it is given that there is a triangle MNO and MP is the median?

Ans: $M P=\sqrt{\dfrac{2 M N^{2}+2 M O^{2}-N O^{2}}{4}}$

Q2. Find the length of median AD if we have the coordinates of triangle ABC as A(1,0), B(0,1), C(1,1)

Ans: $\dfrac{\sqrt{5}}{2}$

Q3. Given statement is true or false i.e. point where median meets opposite sides which is the midpoint of that line.

Ans: True

Q4. For any triangle, the centroid is the point of concurrency of the ____________ of the triangle

Ans: Medians

Q5. How many medians do a triangle have?

Ans: Every triangle has 3 medians

Summary

In geometry, the median of a triangle is the line segment that connects one vertex to the middle of the other side, dividing it in half. Each vertex of a triangle has the same number of medians, which all cross at the triangle's centroid. A median cuts any angle at an angle at the vertex of an isosceles or equilateral triangle whose two adjacent sides are of equal length. Since the corresponding elements of congruent triangles are congruent, the medians of congruent triangles are equal if the two triangles are congruent. Students can become well-versed only by practising many examples of the median of a triangle sum.