




Step-by-Step Guide: Find LCM Using Prime Factorization
A whole number higher than 1 whose only factors are 1 and itself is referred to as a prime number. A whole number that may be split evenly into another number is referred to as a factor. 2, 3, 5, 7, 11, 13, 17, 19, 23 and 29 are the first few prime numbers. Any number can be represented as a sum of prime numbers using prime factorisation.
LCM is short for the Least Common Multiples of two or more numbers. As the name suggests, it's a function that finds the least common multiple between two numbers. So, how do you figure out what LCM is? Find out how to find LCM by Prime Factorization Method and in between the article LCM by prime factorisation method worksheet has been added to check the understanding in the article below.
Methods of Prime Factorization
Using the Tree Method
Use any number from the provided number's factor pair to make two branches, and if a factor is prime, circle it.
If a factor is not prime, continue by writing it as the product of a factor pair.
The sum of circled primes is a composite number.
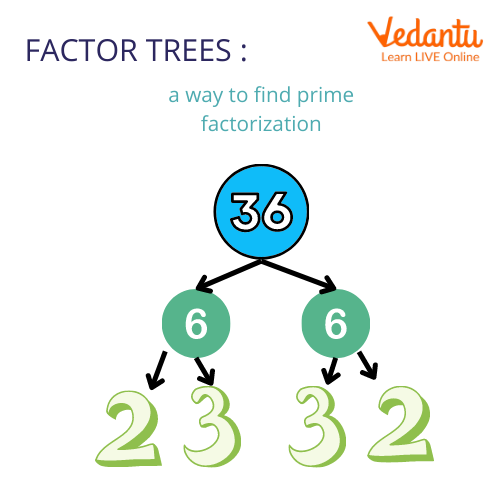
Factor Tree of 36
Using the Ladder Method
The given number is divided by the smallest prime possible and is divided until the number stops dividing.
Keep going until the quotient is prime.
The sum of all the primes at the bottom, sides, and top of the ladder is the composite number.
LCM (Least Common Factor)
A number that is a multiple of both numbers is referred to as a common multiple of two numbers.

Full Form of LCM
Let's say we're looking for multiples of 10 and 25 that are frequently seen. The first few multiples of each integer can be listed. The next step is to find multiples that appear on both lists; these are known as common multiples.
10: 10, 20, 30, 40, 50, 60, 70, 80,90, 100, 110, 120
25: 25, 50, 75, 100, 125
50 and 100 can be seen in both rankings. They are regular multiples of the numbers 10 and 25. If we kept on with the list of multiples for each, we would discover more frequent multiples.
The least common multiple (LCM) is the smallest number which is a multiple of two numbers (LCM). Thus, 50 is the lowest LCM for 10 and 25.
Steps to Calculate LCM by Listing Method
List the initial range of each number's multiples.
Search for multiples that appear on both lists. Write out additional multiples for each number if there aren't any common multiples in the lists.
Find the least quantity on both lists, i.e., LCM number.
How to Find LCM by Prime Factorization Method
Applying the prime factors of two numbers is another method for determining the least common multiple. The steps to be followed to calculate the LCM by the prime factorisation method are as follows:
Finding each number's prime factorisation is the first step in computing the LCM using the prime factors approach.
When you write each number as a product of primes, try to align the primes vertically.
Bring each column's primes down.
To obtain the LCM, multiply the variables.
Below are a few LCM examples with answers and practice problems given on the LCM by the prime factorisation method.
LCM Examples with Answers
Example 1. Calculate the LCM of 15, 20 and 60
Ans: Steps to be followed to calculate LCM are :
1. Finding each number's prime factorisation-
Therefore, 15 = 3, 5
20 = 2, 2, 5
60 = 2, 2, 3, 5
Try to align the primes vertically.
15 = 3, 5
20 = 2, 2, 5
60 = 2, 2, 3, 5
2. Bring each column's primes down.
Therefore- 2, 2, 3, and 5 will be the numbers
3. To obtain the LCM, multiply the variables
Multiplying $2\times 2\times 3\times 5 = 60$
Therefore, LCM will be 60.
Example 2. Calculate the LCM of 50 and 100.
Ans: Steps to be followed to calculate LCM are-
Finding each number's prime factorisation-
$50 = 2\times 5\times 5$
$100 = 2\times 2\times 5\times 5$
Try to align the primes vertically
$50 = 2\times 5\times 5$
$100 = 2\times 2\times 5\times 5$
Bring each column's primes down.
Therefore-2,5, 5 will be the numbers
To obtain the LCM, multiply the variables
Multiplying $2\times 5\times 5=50$
LCM by Prime Factorization Method Worksheet:
Q 1. Calculate the LCM of 15 and 35.
Ans: 105
Q 2. What will be the LCM of 55, 88?
Ans: 440
Q 3. Find the LCM of 60, and 72.
Ans: 360
Summary
In the given article, we have discussed calculating LCM by the prime factorisation method. Therefore, first, we learned about the meaning of prime factorisation and methods of factorisation. Later LCM was calculated by using the prime factorisation method. An LCM by prime factorisation method worksheet is also given to test your knowledge.
FAQs on LCM by Prime Factorization Method Explained
1. What is the LCM of 21 and 49?
21 = 3 × 7.
49 = 7 × 7 = 72.
= 3 × 72 = 3 × 7 × 7 = 147
The required least common multiple (L.C.M) of 21 and 49 = 98
2. How the prime number is different from a composite number?
A prime number has exactly two elements, namely '1' and the number itself. A composite number has more than two elements, which indicates that it can be divided by at least one positive integer in addition to 1 and the number itself. The number one is not a prime or composite number.
3. What will be the LCM for 5, 4 and 16 by using the prime factorisation method?
5 = 5 × 1
4 = 2 × 2
16 = 2 × 2 × 2 × 2 = 24
= 24 × 5 = 2 × 2 × 2 × 2 × 5 = 80
The required least common multiple (L.C.M) of 5, 4 and 16 = 80.























