How to Convert Ratio Into Number

How to Convert Ratio Into Number

Ratio, in math, is a term that is used to compare different numbers. It is used to indicate how big or small a quantity is when compared to another.

We will study how we can convert a ratio into a number, or, we can say, a whole number. Let's break it down by solving the examples with steps provided below in the given examples.

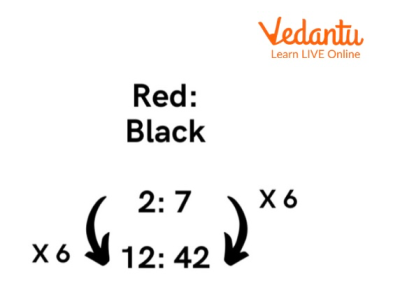
Ratio

How to Simplify Fraction Ratios

How to Find Ratio of 3 Fractions

1. Convert the ratio \[\frac{1}{5}:\frac{1}{3}\] into the whole number ratio or the ratio in its simplest form?

Ans: Given, the ratio is \[\frac{1}{5}:\frac{1}{3}\].
Now, we need to convert the ratio into the whole number ratio, we need to follow the steps given below:

Step 1 : Let’s find the least common multiple (L. C. M.) of the denominators.
So, As the Denominators are 5 and 3 and then the LCM of denominators is \[5 \times 3\; = {\rm{ }}15\].

Step 2: Multiply the both term of the ratio by the least common multiple (L. C. M.) that is,
\[\frac{1}{5} \times 15:\frac{1}{3} \times 15\]
Step 3: Now, just simplify it. We will get the value \[\frac{{15}}{5}:\frac{{15}}{3} = 3:5\].
Hence, the whole number ratio is \[3:5\].

Example. How to Convert the fractional ratio into the whole number ratio. The fractional ratio is \[\frac{1}{6}:\frac{1}{12}:\frac{1}{9}\]?
Solution:
Given, the fractional ratio is \[\frac{1}{6}:\frac{1}{12}:\frac{1}{9}\].
Now, we need to convert the given ratio into the whole number ratio.

Taking L.C.M of the denominators, we get 36

Multiplying each ratio with 36 we get,
Therefore, the whole number ratio is \[6:3:4\].

How to Convert Fraction Into Ratio

Steps to convert a fraction to a ratio.

• Take the numerator of the fraction as the first term of the ratio.

• Then the denominator is the second term of the ratio, after the colon.

• And lastly, simplify the ratio.

Example 2:

Convert \[\frac{2}{6}\] into a ratio.

The numerator becomes the 1st term. \[2\]

Then the denominator becomes the second term. \[6\]

\[\frac{2}{6}\]

When we simplify we get, \[1:3\]

How to Solve Fraction Ratio

Example 3. Ratio \[1\frac{5}{{12}}:\frac{7}{30}\]

Step 1: Convert mixed fractions to improper fractions

As we can see we have \[1\frac{5}{{12}}\] let’s convert this into proper fraction \[\frac{{12 \times 1 + 5}}{{12}}\] will get \[\frac{{17}}{{12}}\] is our proper fraction.

Step 2: Convert both fractions using the LCM

\[\frac{{17}}{{12}}\] and \[\frac{7}{30}\] the lcm of both fraction is \[60\]

Let’s multiply

\[12{\rm{ }} \times {\rm{ }}5{\rm{ }} = {\rm{ }}60\] and\[17{\rm{ }} \times {\rm{ }}5{\rm{ }} = {\rm{ }}85\], giving us \[\frac{{85}}{{60}}\]

\[30{\rm{ }} \times {\rm{ }}2{\rm{ }} = {\rm{ }}60\]and \[7{\rm{ }} \times {\rm{ }}2{\rm{ }} = {\rm{ }}14\], giving us \[\frac{{14}}{{60}}\]

Step 3: Write the numerator as ratio

This gives us \[84:14\]

Step 4 . Simplify the ratio

As it is already in its lowest form hence , the ration is \[84:14\].

How to Convert Number Into Ratio

Example 4:

In a bag we have 8 blue balls and 12 pink balls. What is the ratio of both?

Ans: to get the ratio we need to divide both terms \[\frac{8}{{12}} = \frac{2}{3}\]

Hence, the ratio is \[2:3\]

Solved Questions

1. What is the number ratio of \[\frac{4}{2}:\frac{8}{3}\]?
Ans: Given in the question, the ratio is \[\frac{4}{2}:\frac{8}{3}\].
Now, to convert the ratio into the whole number ratio, we need to follow the steps given below:

Step 1: Find the least common multiple (L. C. M.) of the denominators.
So, the Denominators are 2 and 3 and the LCM of the denominators is \[2 \times 3\; = {\rm{ }}6.\]

Step 2: Multiply each term of the ratio by the least common multiple (L. C. M.) that is,
\[\frac{4}{2} \times 6:\frac{8}{3} \times 6\]
Step 3: Now, simplify it. So the value is \[\frac{{24}}{2}:\frac{{48}}{3} = 12:16\].
Thus, the whole number ratio is \[12:16\].

2. What is the number ratio of the fractional ratio value is \[\frac{1}{5}:\frac{1}{10}:\frac{1}{20}\]?

Ans:
As given in the question, the fractional ratio is \[\frac{1}{5}:\frac{1}{10}:\frac{1}{20}\].
L.C.M of the denominators are 20
Now, multiply each ratio with 20. We get,
Therefore, the whole number ratio is \[4:2:1\].

Summary

We have discussed the ratio and how it is solved in a variety of contexts, including whether it is an improper fraction, mixed fraction, number, etc. by resolving many examples using answers to questions.