Horizontal Multiplication

Never heard of it? Guess what, you have used it before! Horizontal multiplication is a method we use to multiply numbers and binomials. Have you ever tried multiplying binomials? But couldn’t do it because it was confusing? Well then, you are on the right page, today, we will learn about how to multiply binomials using the horizontal method. Don’t know how to start? No worries, today we will learn about multiplying two-digit numbers first, and then we will learn about binomials. It might be confusing now but by the end of this article, you will be able to use this method easily.

Multiplying Two - Digit Numbers

Let’s start with multiplying two-digit numbers for your understanding.

For example, let’s multiply 22 x 41.

To simplify this, we will write 22 as (20 + 2) and 41 as (40 + 1)

So, now we have: (20 + 2) x (40 + 1)

Looks complicated? Don’t worry, it makes the calculation a lot simpler.

Now, to open the brackets (considering the BODMAS rule, we solve the brackets first), we will multiply the first number (20) of the first bracket by both numbers (40 and 1 separately) of the second bracket.

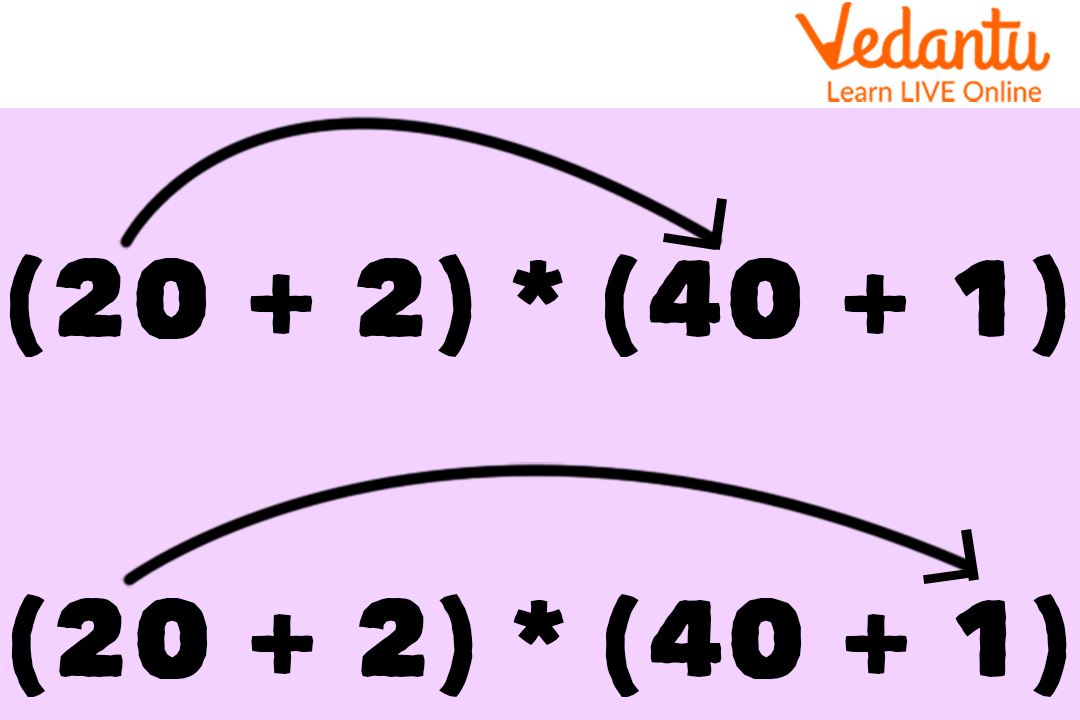
Multiplication of 2-digit Numbers

Which would be (20 x 40 + 20 x 1) and the result would be (800 + 20) = 820.

Now, we will multiply the second number of the first bracket (2) by both numbers of the second bracket (40 and 1 separately).

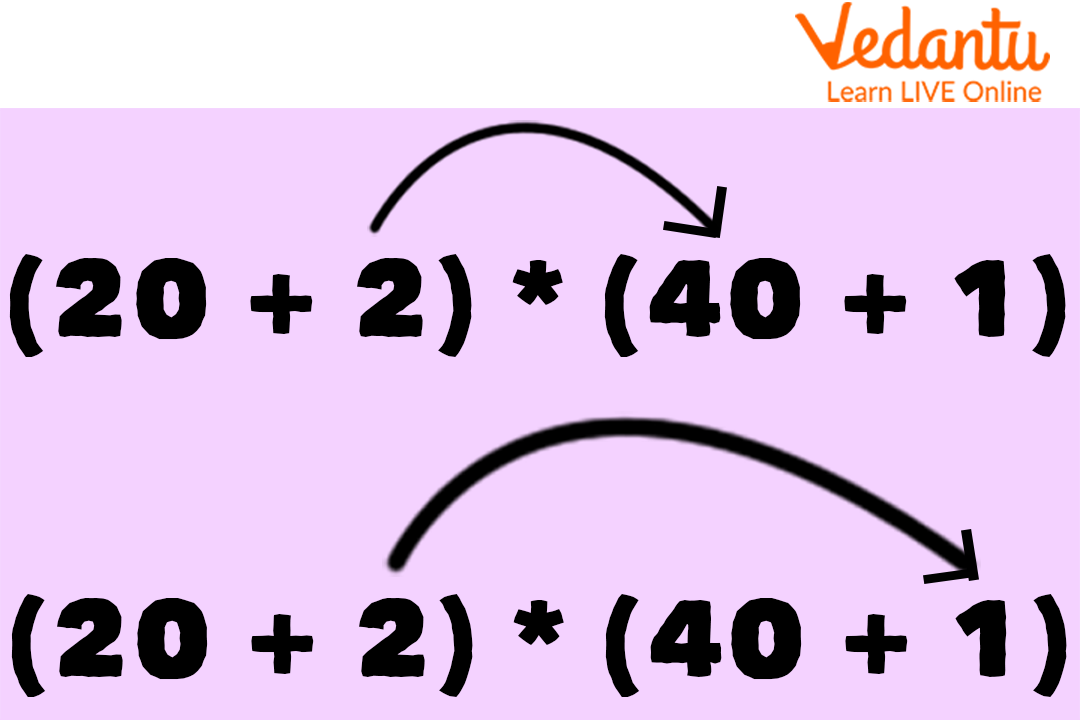
Multiplication of 2-digit Numbers

Which would be (2 x 40 + 2 x 1), which would give (80+2) = 82.

Now to get the final solution, we would add both result numbers, which would give: (820+82) = 902.

Let’s do another example without visualization:
Example: 34 x 45

Solution: (30 + 4) x (40 + 5)

= (30 x 40 + 30 x 5) + (4 x 40 + 4 x 5)

= (1200 + 150) + (160 + 20)

= 1350 + 180

= 1530

Note: Look at the signs of addition and subtraction.

What is a Binomial?

It’s a polynomial expression that consists of two terms with either a plus or minus sign in between. It contains a variable, coefficient, exponents, and constant. For example, $(x+5)$, $(y-10)$, etc.

Multiplying Two Binomials

In this section, we are going to learn how to multiply binomials. Now that you have learned how to multiply two-digit numbers, we will move on to binomial multiplication.

Let’s take an example of $(a+3) \times(a+9)$.

Following a similar method to multiplying two-digit numbers, we will first multiply the first variable from the first bracket to both the variable and the number of the second bracket.

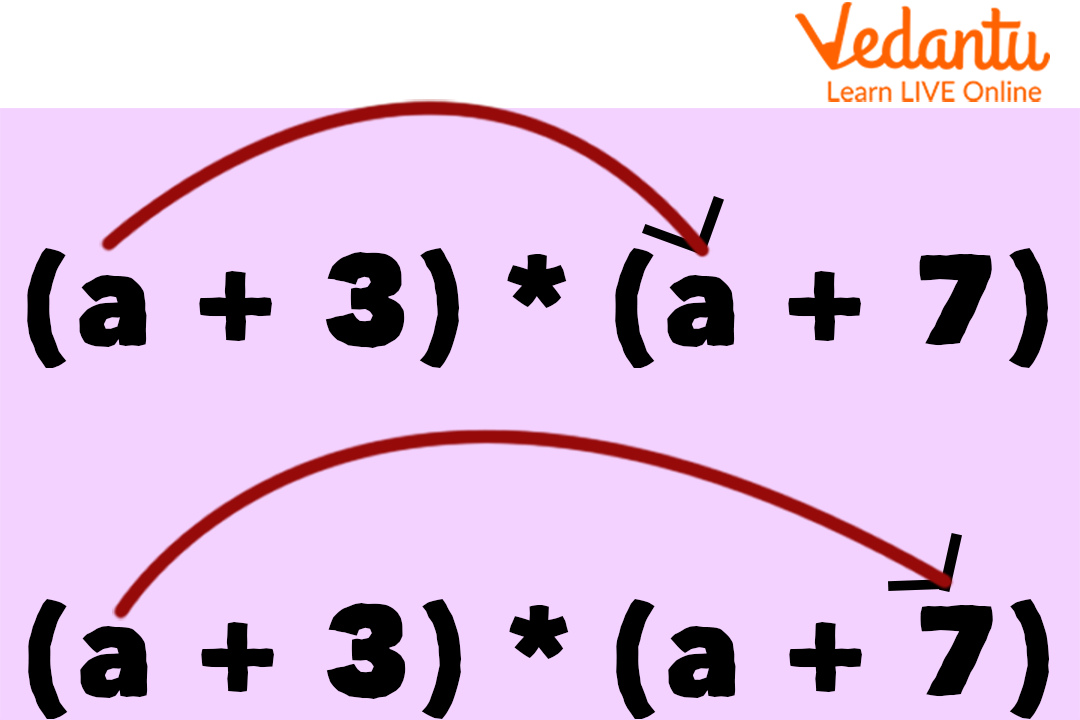
Multiplication of 2 Binomials

Which would give us $(a \times a + a \times 7)$ and that would be $\left(a^2+7 a\right)$.

Now, we will multiply the second digit of the first bracket by both the variable and the number of the second bracket.

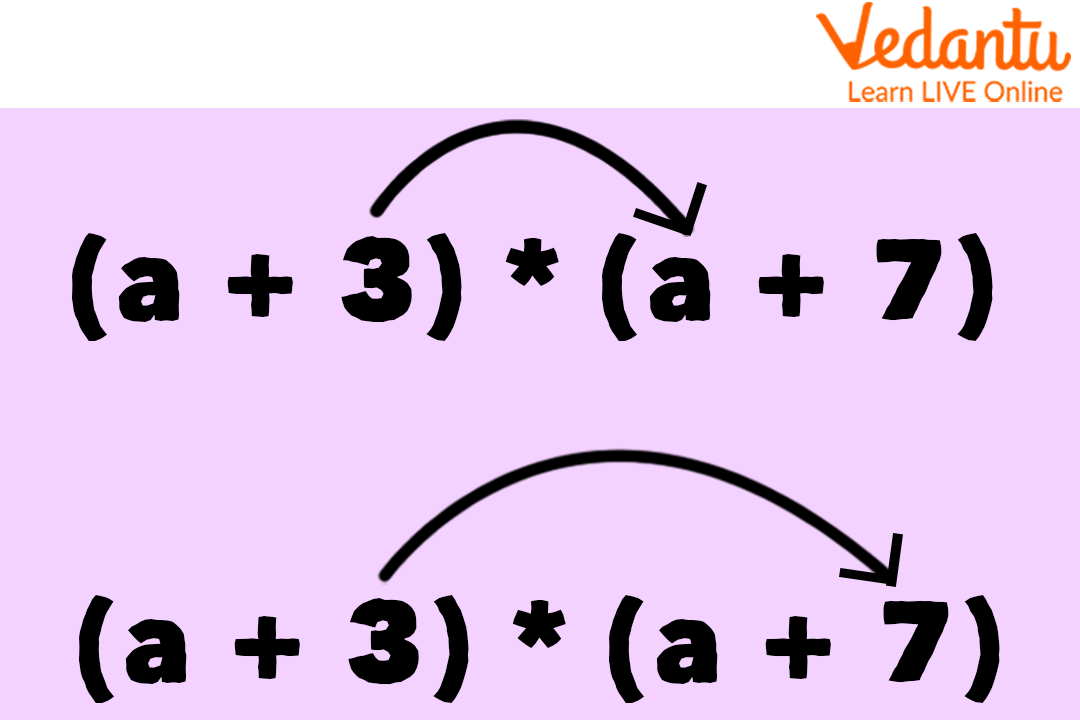
Multiplication of 2 Binomials

Which would give us (3 x a + 3 x 7) and that would be (3a + 21).

To get the final solution, we will add both results:

(Hint: After solving brackets, we will add the like terms)

$=\left(a^2+7 a\right)+(3 a+21)$

$=\left(a^2+7 a+3 a+21\right)$

$=a^2+10 a+21$

Solved Examples

Now that we have learned the horizontal multiplication method for binomials, we will try to solve a few examples.

Example 1: Multiply (x + 1) (x + 2).

Ans: $(x \times x + x \times 2) + (1\times x + 1 \times 2)$

$=(x^2+2 x)+(x+2)$

$=x^2+3 x+2$

Example 2: Multiply (y + 4) (y - 2).

Ans: $(y \times y - y \times 2) + (4 \times y - 4 \times 2)$

$=\left(y^2-2 y\right)+(4 y-8)$

$=y^2+2 y-8$

Example 3: Multiply (a + 4) (a - 8).

Ans: $(a \times a - a \times 8) + (4 \times a - 4 \times 8)$

$=\left(a^2-8 a\right)+(4 a-32)$

$=a^2-4 a-32$

Example 4: Multiply (y + 6) (y + 9).

Ans: $(y \times y + y \times 9) + (6 \times y + 6 \times 9)$

$=\left(y^2+9 y\right)+(6 y+8)$

$=y^2+9 y+6 y+54$

$=y^2+15 y+54 $.

Example 5: Multiply (x + 2) (x - 2).

Ans: $(x\times x - x \times 2) + (2 \times x - 2 \times 2)$

$=\left(x^2-2 x\right)+(2 x-4)$

$=x^2-2 x+2 x-4$

$=x^2-4$

Can you do it too?

Now that we have solved a few examples, let’s see if you can solve some on your own too.

Q 1: Multiply (a + 1) (a - 2).

Ans: $a^2-a-2$

Q 2: Multiply $(y+7)(y-8)$.

Ans: $y^2-y-56$

Q 3: Multiply $(5+x)(x-2)$.

Ans: $x^2+3 x-10$

Q 4: Multiply $(8+y)(y+7)$.

Ans: $y^2+15 y+56$

Q 5: Multiply $(a+5)(a-9)$.

Ans: $a^2-4 a-45$

Summary

The horizontal method is a multiplication method, which is done by arranging the variables and numbers in a horizontal line and then multiplying them step by step, making the calculation easier. First of all, we learned that we need to write the values in a horizontal line, and arrange the question in a way that all like terms are together. Then we saw that we had to apply the BODMAS rule and multiply both values of the first bracket with both values of the second bracket separately. In the end, just combine the result. And there we go, we got the result. To understand these steps more clearly we have added the practice problem too, so after going through this article give it a try!