




Solved Examples: HCF of Three Numbers Explained
The highest number that completely divides two numbers is known as the Highest Common Factor (HCF). The Greatest Common Divisor (GCD) is another name for the Highest Common Factor (HCF) (GCD). The HCF of two numbers can be determined in a variety of methods. Using the prime factorization method is one of the easiest ways to get the HCF of two or more numbers. In this article, we will learn how to find HCF by long division method with some examples.
Steps to Find HCF of 3 Numbers by Using the Long Division Method
Follow the Steps for a better understanding:
Step 1: We first need to find out the HCF of the first two given numbers.
Step 2: Find out the HCF of the third number given and the HCF of the first two numbers that we got from the previous step.
Step 3: We mark the highest factor among which we found common.
Solved Examples
Q1. Find the HCF of 144, 198 and 162
Ans: Using the long division method
First of all, arrange the given numbers in ascending order. Not necessary but preferable.
Let's first find out the HCF of the first 2 numbers which are 144 and 198. i.e. HCF of 144 and 198.
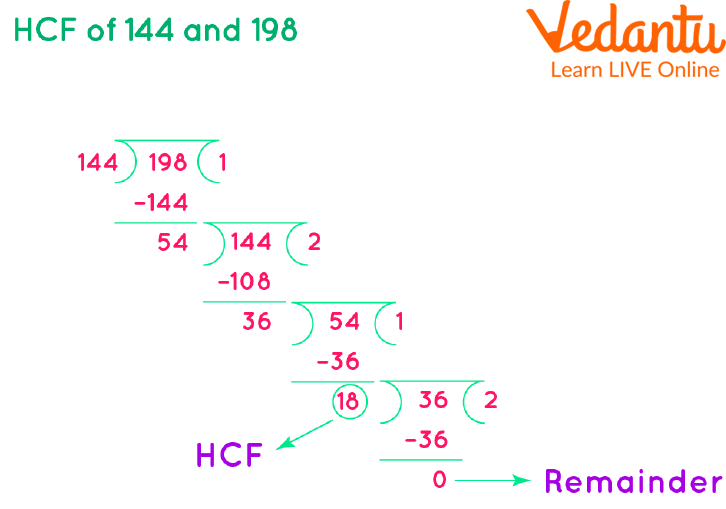
HCF of 144 and 198 by Using Long Division Method
Therfore, the HCF of 144 and 198 = 18
The next step is to find the HCF of 162 and 18

HCF of 162 and 18
So by applying HCF division method, we get HCF of 162 and 18 = 18
Therefore the HCF of all the 3 numbers is
HCF of 144, 198 and 162 = 18
Note: It's Important that the Remainder is Always 0 at the End
Let's try to understand with one more example
Q2. Find the HCF of 729, 864 and 945
Ans: Using the long division method
Let's first find out the HCF of the first 2 numbers which are 729 and 864. i.e. HCF of 864 and 729.
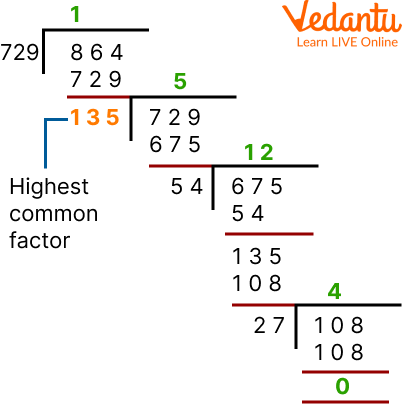
HCF of 864 and 729
The HCF of HCF of 864 and 729 = 27
The next step is to find the HCF of the third number that is given which is 945 and the HCF of the first two numbers which is 27.
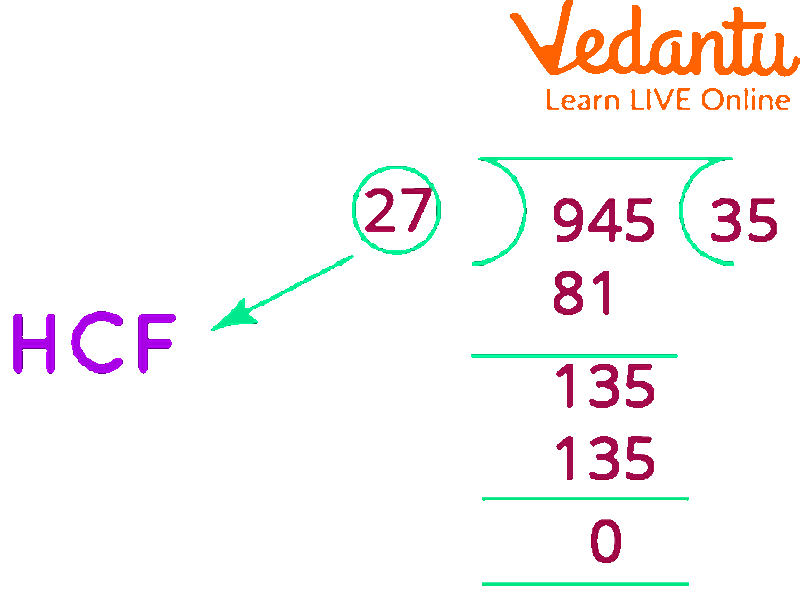
HCF of 945 and 27
HCF of 945 and 27 = 27
Therefore the HCF of all the 3 numbers is 27.
HCF of 729, 864 and 945 = 27
Practice Problem
Q1. Find the HCF of 30, 45 and 150
Ans: 15
Q2. Find the HCF of 126, 162 and 180
Ans: 18
Q3. Find the HCF of 300, 270 and 9
Ans: 3
Q4. Find the HCF of 78, 98 and 108
Ans: 2
Q5. Find the HCF of 702, 153 and 405
Ans: 9
Summary
This article has tried to explain the detailed steps of how to find HCF by using the long Division method for 3 given numbers. To find the HCF by division method the first step is to divide the larger number by the smaller number and then the remainder becomes the divisor and divide the smaller number until the remainder is zero. So, read the whole content nicely and do the solved examples present here in this article.
FAQs on Simple Steps to Find HCF of 3 Numbers
1. How do you find the HCF of 3 numbers?
To find the Highest Common Factor (HCF) of 3 numbers, follow these steps:
- First, find the HCF of any two numbers using either the prime factorization method or the division method.
- Then, find the HCF of the result with the third number. Mathematically, if the numbers are $a$, $b$, and $c$, then $\text{HCF}(a, b, c) = \text{HCF}(\text{HCF}(a, b), c)$.
2. What is the HCF of 136, 170, and 255?
To calculate the HCF of 136, 170, and 255:
- First find the HCF of 136 and 170:
Prime factorization: 136 = $2^3 \times 17$, 170 = $2 \times 5 \times 17$
Common factors: 2 and 17
HCF(136, 170) = 2 × 17 = 34 - Next, find the HCF of 34 and 255:
34 = 2 × 17, 255 = 3 × 5 × 17
Common factor: 17
3. What is the HCF of 36, 42 and 48?
Prime factorization:
- 36 = $2^2 \times 3^2$
- 42 = $2 \times 3 \times 7$
- 48 = $2^4 \times 3$
Hence, HCF of 36, 42, and 48 is 6. For more such HCF practice problems and explanations, Vedantu provides comprehensive study modules aligned with different class levels.
4. What is the HCF of 12 45 and 75?
Factorization:
- 12 = $2^2 \times 3$
- 45 = $3^2 \times 5$
- 75 = $3 \times 5^2$
Therefore, HCF of 12, 45, and 75 is 3.
Students can further sharpen their problem-solving skills using Vedantu’s interactive HCF worksheets and doubt clearing sessions.
5. How can HCF be useful in real-life situations involving three items?
The HCF of three numbers is useful in real-life contexts such as:
- Dividing objects (like sweets, books, or ribbons) into equal groups with no remainder.
- Organizing events or schedules to avoid any overlap when multiple cycles are involved.
- Solving problems where you must split quantities into the largest possible identical sections.
6. What are the different methods to find the HCF of 3 numbers?
There are several methods to find the HCF of three numbers:
- Prime Factorization: List out the prime factors for each number and identify the common factors.
- Division Method: Use the HCF of two numbers first, then with the third.
- Euclidean Algorithm: A step-wise approach using division, repeatedly applying $\text{HCF}(a, b, c) = \text{HCF}(\text{HCF}(a, b), c)$.
7. What is the difference between HCF and LCM of three numbers?
HCF (Highest Common Factor) refers to the largest number that divides all the given numbers exactly, while LCM (Least Common Multiple) is the smallest number that is a multiple of all the numbers.
For three numbers:
- Use HCF when you need to split or arrange items into maximum equal groups.
- Use LCM to find timings or quantities matching multiple cycles or repetitions.
8. Can you use the HCF of 3 numbers to simplify fractions?
Yes, the HCF of three numbers is very useful for simplifying fractions, especially when reducing ratios or dividing quantities into simplest forms.
- For example, to simplify the ratio 12:45:75, divide each number by their HCF (which is 3), resulting in 4:15:25.
9. Are there any tricks for finding the HCF of large numbers quickly?
One of the quickest ways to find the HCF of large numbers is the Euclidean algorithm:
- Subtract the smaller number from the larger repeatedly, or use division with remainder until you get zero. The last non-zero remainder is the HCF.
- Apply this pairwise among the three numbers.























