Factors of 225

As we all know that 225 is a composite number, it has some proper factors i.e., factors other than 1 and 225. A total of 9 integers are there that are factors of 225 viz. 1, 3, 5, 9,15, 25, 45, 75, 225. Naturally, a prime factor of 225 is a factor of 225 which is also a prime number; hence from the above list of factors, we can see that the prime factors of 225 are 3 and 5 only. Moreover, 225 is a perfect square i.e., each prime factor of 225 occurs in pairs. The square root of 225 is 15. Also, the pair factors of 225 are: (1,255), (3,75), (5,45), (9,25), and (15,15).

Definition of a Factor of an Integer

A factor of an integer is another integer that can divide the integer without leaving any remainder i.e., an integer F is said to be a factor of another integer N if F completely divides N. For example, the integers 2 and 3 can divide the integer 6 without leaving any remainder; so, 2 and 3 are factors of 6.

A factor can be both a positive and a negative integer that we will understand by the same example above. As 2 is a factor of 6, -2 is also a factor of 6 because $6\div (-2)=-3$ which is also an integer i.e., (-2) completely divides 6 without leaving any remainder. Similarly, (-3) is also a factor of 6. Thus, we can say that if F is a factor of N, then -F is also a factor of N. Here, in this topic, we will mostly talk about the positive factors of 225.

Proper and Improper Factors

As 1 divides every integer and each integer divides itself, by definition of a factor, every integer N has at least 2 factors: 1 and N itself. These are called the Improper Factors of N. All other factors of N are called the Proper Factors of N. For example, 1, 6 are the improper factors of 6 and $2,\text{ }3$ are proper factors of 6.

Prime Factors

As the name suggests, a prime factor of an integer N is an integer P that is a factor of N as well as a prime number. For example, 2 and 3 are prime factors of 6 as they are factors of 6, and also, they are prime numbers.

Pair Factors

A pair of integers $\left( {{F}_{1}},{{F}_{2}} \right)$ are said to be a Pair Factors of an integer $N$., if firstly, they are factors of $N$ and secondly, their product yields $N$ i.e., ${{F}_{1}}\times {{F}_{2}}=N$. For example, as $1,\text{ }2,\text{ }3,\text{ }6$ are factors of 6 and $1\times 6=6$, $2\times 3=6$; (1,6) and (2,3) are pair factors of 6.

What are the Factors of 225?

Factors of 225 are the integers that completely divide it without leaving any remainder. Let us first find out the integers that fully divide 225:

$225\div 1=225$ $225\div 225=1$

$225\div 3=75$ $225\div 75=3$

$225\div 5=45$ $225\div 45=5$

$225\div 9=25$ $225\div 25=9$

$225\div 15=15$

Hence, by definition, 225 has a total of 9 factors: $1,\text{ }3,\text{ }5,\text{ }9,\text{ }15,\text{ }25,\text{ }45,\text{ }75,\text{ }225$.

If we consider negative factors also, then 225 has a total of 18 factors, viz.,$\pm 1,\text{ }\pm 3,\text{ }\pm 5,\text{ }\pm 9,\text{ }\pm 15,\text{ }\pm 25,\text{ }\pm 45,\text{ }\pm 75,\text{ }\pm 225$.

Method of Finding the Factors of 225

In this section, we will learn how to find the factors of 225. There are several methods of finding the factors of an integer. Here, we will follow the Division Method. In this method, we will divide 225 successively by the integers starting from 1, 2, 3, and so on and whenever we get the remainder 0, then the corresponding divisor and quotient will be treated as the factors of 225. This process continues till any one of the numbers is repeated.

In Step 15, the quotient and the divisor are the same i.e., 15. This means that all the factors of 225 have been obtained. So, we must stop the process.

Hence, the factors of 225 are: $1,\text{ }225,\text{ }3,\text{ }75,\text{ }5,\text{ }45,\text{ }9,\text{ }25,\text{ }15$.

Moreover, notice that in Step-15, $225=15\times 15$ i.e., the number repeats itself as a factor. Hence, 225 is a perfect square.

Prime Factorisation of 225: Factor Tree

A prime number is a positive integer P that has only two factors (not considering the negative factors here). For example, $2,\text{ }3,\text{ }5$etc.

One of the most useful methods of finding the factors of an integer is prime factorization. In this method, we factorize an integer only into its prime factors. Let us find the prime factorization of 225. This can be obtained by the following few steps.

1. In the first step, we take the smallest prime number 2, and check whether it divides 225 or not. But 2 does not divide 225 completely as it leaves a remainder of 1 $(225=2\times 112+1)$ while dividing 225. Therefore, 2 cannot be a factor of 225.

2. After that, we look for the next prime number which is 3, and similarly check if it divides 225 completely or not. As $225=3\times 75$, on dividing 225 by 3, we get the quotient 75 and the remainder 0. Therefore, 3 is a prime factor of 225.

3. Next, we take the quotient 75 obtained in the second step and check whether 3 divides 75 or not. Clearly, 3 divides 75 and $75\div 3=25$.

4. Now, we proceed for the above quotient 25 and the prime number 3. But $25=3\times 8+1$; that means 3 does not divide 25.

5. So, we proceed for the next prime number 5 and easily obtain that $25\div 5=5$. Hence, 5 is a prime factor of 225.

6. Next, we take the quotient 5 obtained in the above step and get $5\div 5=1$.

As we have got 1 as a quotient at the end, we cannot proceed further because 1 is not a multiple of any prime numbers.

In brief, we perform the following in the above six steps:

$225\div 3=75$

$75\div 3=25$

$25\div 5=5$

$5\div 5=1$

Therefore, the prime factors of 225 are 3 and 5. Moreover, the prime factorization of 225 is $225=3\times 3\times 5\times 5$. This can be easily understood by the following factor tree of 225:

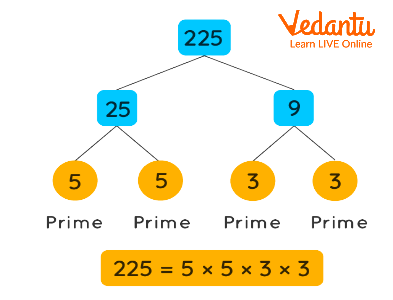
225 Factor Tree

Now, we can find all the factors of 225 by prime factorization as follows:

• First, write all the prime factors as many times as they occurred: $3,\text{ }3,\text{ }5,\text{ }5$.

• Now, multiply each of these number with another number and get: $3\times 3=9$, $3\times 5=15$, $5\times 5=25$, $3\times 3\times 5=45$, $5\times 5\times 3=75$, $3\times 3\times 5\times 5=225$. Thus, the factors obtained are: $9,\text{ }15,\text{ }25,\text{ }75,\text{ }45,\text{ }225$.

• Also, 1 is a factor.

• Now, list all the factors. Hence, all the factors of 225 are: $1,\text{ }3,\text{ }5,\text{ }9,\text{ }15,\text{ }25,\text{ }45,\text{ }75,\text{ }225$.

Factors of 225 in Pairs

We have,

$225=1\times 225$

$225=3\times 75$

$225=5\times 45$

$225=9\times 25$

$225=15\times 15$

Hence, by definition, the pair factors of $225$ are: (1,225), (3,75), (5,45), (9,25) and (15,15).

Interesting Facts

• 225 is a perfect square. The square root of 225 is 15.

• The sum of all the factors of 225 is 403.

• Did you know that there are no factors of N in between $\dfrac{N}{2}$ and N.

  
  

Solved Examples

1. There are 135 pens and 225 exercise books to be distributed among the students of class VII. What should be the maximum number of students so that each student gets an equal number of pens and exercise books?

Solution:

Here, the maximum number of students should be the largest integer that divides both 135 and 225.

So, the required number of students will be the H.C.F. of 135 and 225.

By prime factorization, we get:

$135=3\times 3\times 3\times 5$

$225=3\times 3\times 5\times 5$

Hence, the Highest Common Factor of 135 and 225 is $3\times 3\times 5=45$.

Therefore, the maximum number of students should be 45.

2. What is the sum of all factors of 225?

Solution: The factors of 225 are: $1,\text{ }3,\text{ }5,\text{ }9,\text{ }15,\text{ }25,\text{ }45,\text{ }75,\text{ }225$. So, the sum of all factors of 225 is $1+3+5+9+15+25+45+75+225=403$.

Practice Questions

1. Find the largest factor of 225 which is a perfect square.

2. Find H.C.F. of 45 and 225.

3. Is there any factor of 225 which lies between 112 and 225? Justify your answer.

4. Find the average factor of 225.

5. Is 20 a factor of 225?

Answer

1. 225

2. 45

3. No

4. 44.78

5. No

Conclusion

As discussed earlier the factors of 225 can be obtained by several methods such as the Division Method, Prime Factorization Method, etc. It has a total of 6 factors: $1,\text{ }3,\text{ }5,\text{ }9,\text{ }15,\text{ }25,\text{ }45,\text{ }75,\text{ }225$ among which only 2 prime factors, 3, 5, are there. Prime factorization of 225 is $225=3\times 3\times 5\times 5$. 225 is a perfect square; the square root of 225 is 15. Try practicing the questions from this article on your own.