How to Find Factors Using Multiplication Method with Steps and Examples
Factors can be defined as the numbers that divide a number without leaving any remainder. These numbers are usually whole numbers, which, when multiplied with other whole numbers, give products. We can find the factors by using methods like factorization, multiplication tables, and division. The first and simplest method for finding factors is by using the multiplication method. Today you will learn to find factors by the multiplication method.
What are Factors and Multiplication Facts?
As said above, when two whole numbers are multiplied to give us a product, the whole numbers are called the factors. For example, have a look at the image below.
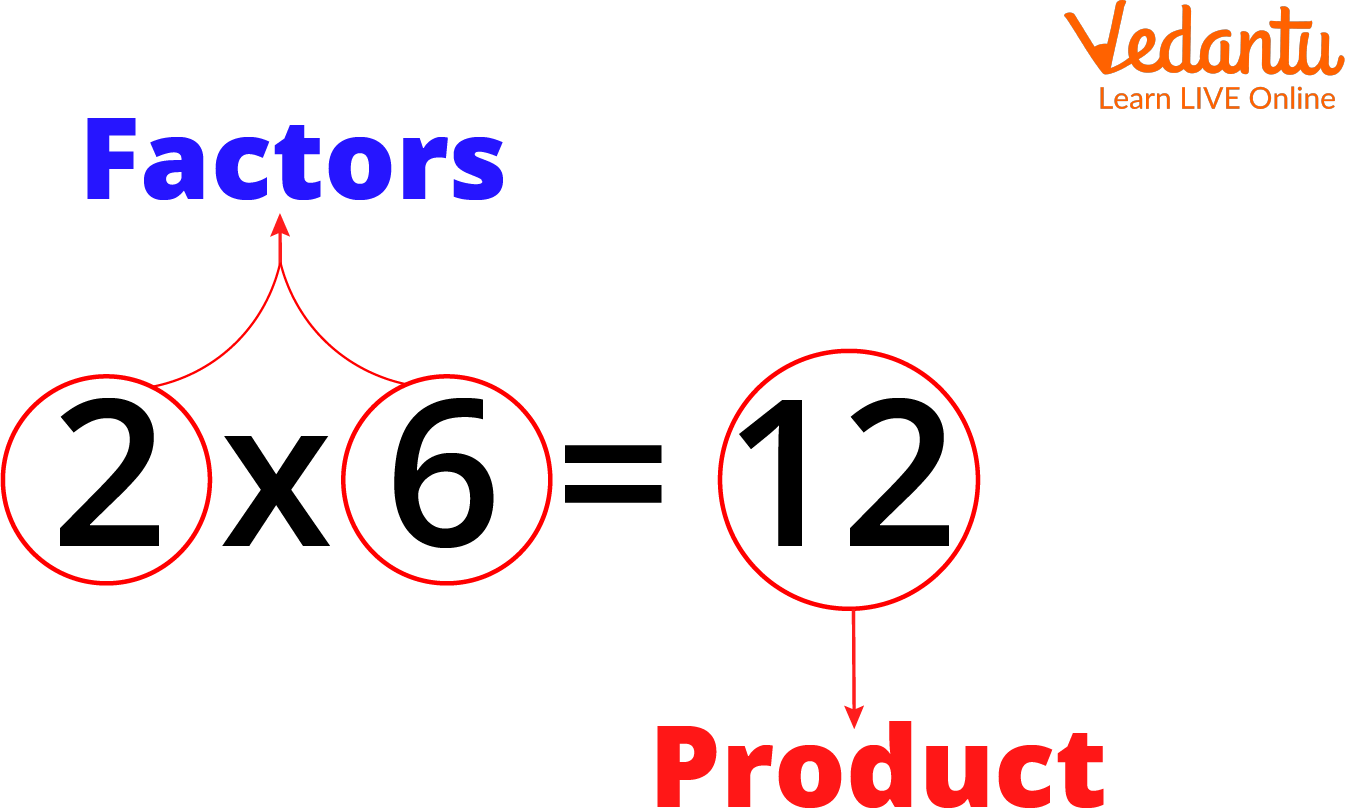
Factors and Their Product
In the image above, you can see that 2 and 6 are multiplied together to give 12 as a product, so we can write that 2 and 6 are the factors of 12. If you know about multiplication, you must already know that 2 is a multiplicand, 6 is the multiplier, and 12 is the product. If you need to learn about multiplicands and multipliers, observe that 2 in the above picture is multiplied by 6 and gives 12. So, 2 is the multiplicand, 6 is the multiplier, and 12 is the product. Therefore, a multiple or a multiplication factor is a product of multiplication factors.
And according to the definition of factor, both multiplicand and multiplier are factors. The multiplicand and multiplier can also change places, as shown below.
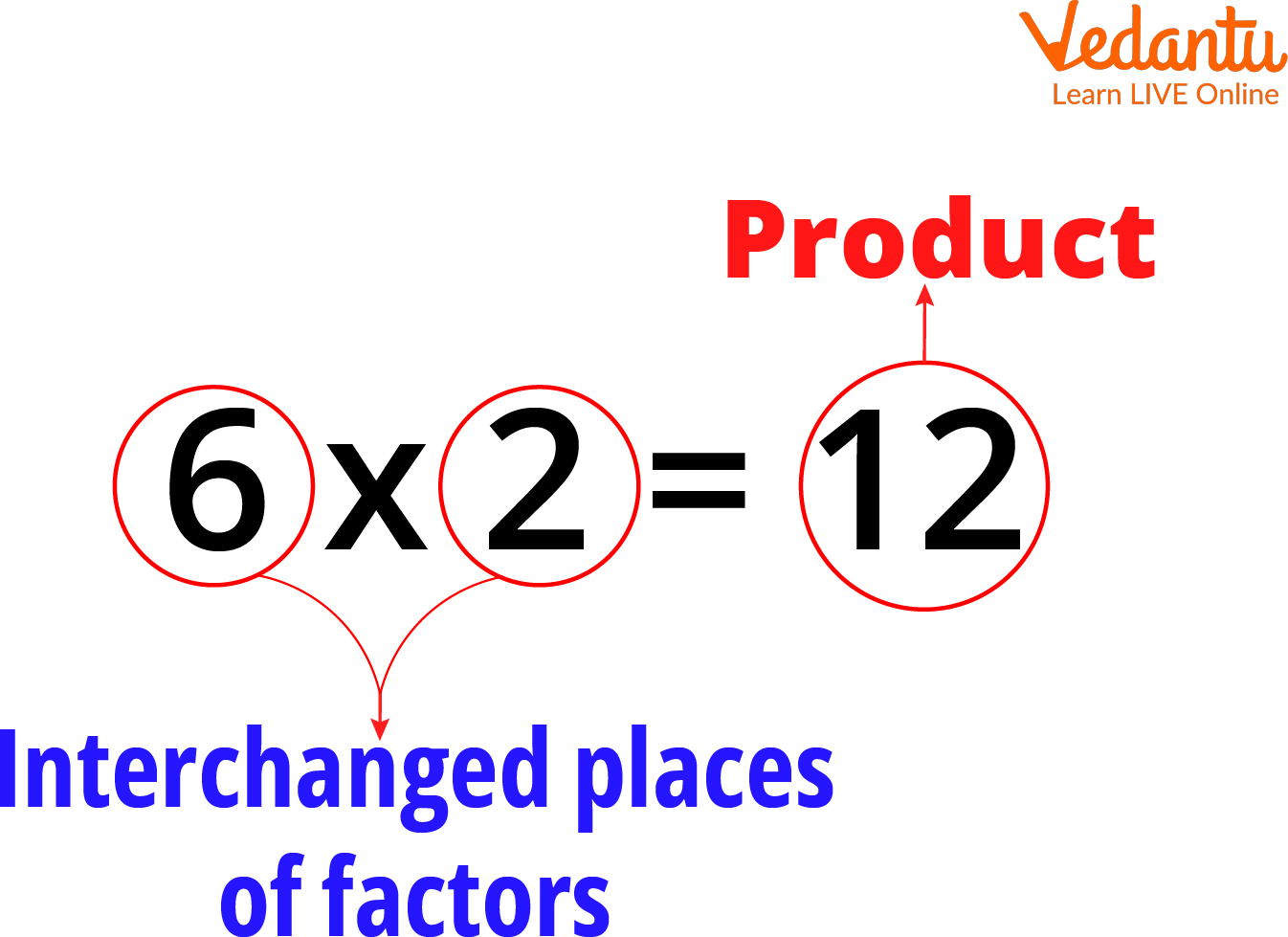
Changed Places of Multiplicand and Multiplier
So, this is what a multiplication factor is. On the other hand, the product is known as multiple or multiplication facts. This is how you can identify factors and multiplication facts.
How to Find Factors and Multiples by Using Multiplication Facts?
Have a look at the chart below. You can see that all the multiplication results are 10, and these are the multiplication facts. You can see that 1, 2, 5, and 10 are multiplied to get the multiplication fact of 10. Hence, 1, 2, 5, and 10 are the factors of 10.
Image: Factors and multiples chart,
Therefore, to calculate the factors using multiplication facts, you have to write the multiplication facts and their multiples. First, you must start with one because one is a factor in every number. Then check and proceed with every number one by one, as done above. This is how you can use the multiplication method to find factors with the help of multiplication facts.
Examples of Factors and Multiplication Facts
Let us see some examples where you can use multiplication facts to find factors.
(i) Determine the factors of 15
since one has to always start with one,
$1 \times 15 = 15$.
You can see that 1 and 15 are factors of 15.
We can also write that
$3 \times 5 = 15$
Hence, the above expression was put in place of 15 on the left side.
Thus, the factors of 15 are 1, 15, 3, and 5.
(ii) Find factors of 24.
As always, one has to start with 1.
$1 \times 24 = 24$
You can expand the above expression by checking the divisibility one by one,
$2 \times 12 = 24$
One more expression that can be written is,
$3 \times 8 = 24$
Therefore, the factors of 24 are 1, 2, 3, 8, 12, and 24.
Conclusion
You have learnt that we can find factors using division and multiplication. You have learnt about factors, multiplication facts, multiplicands, multipliers, and multiples. The product of multiplication is called multiple, and multiplicands and multipliers are called factors. Multiplication facts determine the factors if you use the multiplication method.
FAQs on Factors by Multiplication Method in Mathematics
1. What is the factors by multiplication method?
The factors by multiplication method is a technique used to find the factors of a number by identifying pairs of numbers whose product equals the given number. It involves systematically multiplying whole numbers to see which combinations produce the target number. For example, to find factors of 12:
- 1 × 12 = 12
- 2 × 6 = 12
- 3 × 4 = 12
2. How do you find factors using the multiplication method?
To find factors using the multiplication method, list pairs of numbers that multiply to give the target number. Follow these steps:
- Start from 1 and multiply it with increasing numbers.
- Check which pairs give the exact product.
- Stop when pairs start repeating.
- 1 × 18
- 2 × 9
- 3 × 6
3. What are factor pairs in the multiplication method?
A factor pair is a pair of numbers that multiply together to give a specific number. In the factors by multiplication method, factor pairs are identified by checking multiplication combinations. For example, factor pairs of 20 are:
- (1, 20)
- (2, 10)
- (4, 5)
4. Can you give an example of finding factors by multiplication?
Yes, to find factors of 24 using the multiplication method, identify number pairs whose product is 24. Example:
- 1 × 24
- 2 × 12
- 3 × 8
- 4 × 6
5. Why do we stop checking after reaching the square root of a number?
We stop checking at the square root of a number because factor pairs repeat after that point. For example, the square root of 36 is 6. The factor pairs are:
- 1 × 36
- 2 × 18
- 3 × 12
- 4 × 9
- 6 × 6
6. What is the difference between factors and multiples?
The difference is that factors divide a number exactly, while multiples are the results of multiplying a number by whole numbers. For example, for 5:
- Factors of 5: 1 and 5
- Multiples of 5: 5, 10, 15, 20, ...
7. How do you find factors of a large number using multiplication?
To find factors of a large number, test divisibility from 1 up to its square root and record valid multiplication pairs. Steps:
- Start with 1.
- Check divisibility systematically.
- List factor pairs.
- 1 × 50
- 2 × 25
- 5 × 10
8. What are the factors of a prime number using the multiplication method?
A prime number has exactly two factors: 1 and itself. Using the multiplication method, only one pair exists. For example, for 13:
- 1 × 13 = 13
9. What are common mistakes when using the factors by multiplication method?
Common mistakes include missing factor pairs and not checking up to the square root. Key errors to avoid:
- Stopping too early.
- Forgetting to list both numbers in a pair.
- Confusing factors with multiples.
10. How is the multiplication method useful in real life?
The multiplication method helps in arranging objects equally, dividing quantities, and solving algebra problems. It is useful for:
- Grouping items into equal rows.
- Finding dimensions of rectangles.
- Simplifying fractions.
