Area of Triangle with 3 Points in Coordinate Geometry

Due to the word "tri," which stands for "three," the polygon with three sides is referred to as a triangle. Additionally, the name of the polygon suggests that it contains three angles. A polygon having three edges & three vertices is called a triangle. It is one of the fundamental geometric shapes.

The symbol for a triangle having vertices A, B, and C is ∆ABC. Triangles can be found in a variety of everyday objects, such as sandwiches, traffic signs, clothes hangers, and billiards racks. The area can be calculated using the formula "a = $\dfrac{bh}{2}$."

Triangle

Area of a Triangle with Three Points

Area of Triangle with 3 Points Formula

In a two-dimensional plane, the area of a triangle is the area that it completely encloses. A triangle is a closed shape with three sides and three vertices, as is common knowledge. The entire area occupied by a triangle's three sides is referred to as its area. Half of the product of the triangle's base and height provides the general formula for calculating the area of the triangle.

Area of a Triangle

Area of Triangle with Coordinates of the Vertices

Triangle Vertices Formula

An ordered pair of real integers, known as the coordinates of that location, can be used to represent a point in a plane (sometimes referred to as a cartesian plane or a coordinate plane). Coordinate geometry is the area of mathematics that deals with employing coordinate systems to solve geometrical problems.

We will look at how to determine the area of the triangle using vertices if the triangle's coordinates are given. The area of the triangle is calculated if the triangle's coordinates are $\left(x_{1}, y_{1}\right), \left(x_{2}, y_{2}\right)$, and $\left(x_{3}, y_{3}\right)$.

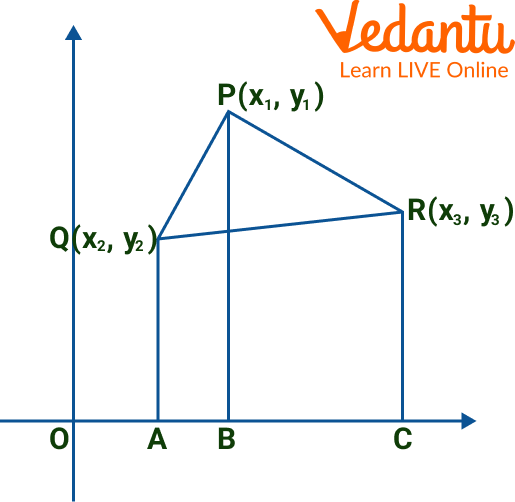
Area of a Triangle with Coordinates

Area of $\Delta \mathrm{PQR}=\dfrac{1}{2}\left[x_{1}\left(y_{2}-y_{3}\right)+x_{2}\left(y_{3}-y_{1}\right)+x_{3}\left(y_{1}-y_{2}\right)\right]$

Sample Problems

1. If A(1, 2), B(4, 2), and C(5, 5) are the vertices of the ABC, respectively. What is the area of the ABC?

Ans: Here, the points are given as

$\left(x_{1}, y_{1}\right)=(1,2)$

$\left(x_{2}, y_{2}\right)=(4,2)$

$\left(x_{3}, y_{3}\right)=(5,5)$

As we know Area of $\Delta \mathrm{ABC}=\dfrac{1}{2}\left[x_{1}\left(y_{2}-y_{3}\right)+x_{2}\left(y_{3}-y_{1}\right)+x_{3}\left(y_{1}-y_{2}\right)\right]$

Substituting the values, we get

$=\dfrac{1}{2}[1(2-5)+4(5-2)+3(2-2)]$

$=\dfrac{1}{2}[(-3)+12+(0)]$

= Area = 4.5

Thus, the area of ABC is 4.5 sq units.

2. Find the area of the triangle formed by the points $(5,2),(-9,-3)$ and $(-3,-5)$

Ans: Let $\mathrm{A}\left(\mathrm{x}_1, \mathrm{y}_1\right)=(5,2), \mathrm{B}\left(\mathrm{x}_2, \mathrm{y}_2\right)=(-9,-3)$ and $\mathrm{C}\left(\mathrm{x}_3, \mathrm{y}_3\right)=(-3,-5)$ be the points of a triangle.

As we know Area of $\Delta \mathrm{ABC}=\dfrac{1}{2}\left[x_{1}\left(y_{2}-y_{3}\right)+x_{2}\left(y_{3}-y_{1}\right)+x_{3}\left(y_{1}-y_{2}\right)\right]$

Now by using the formula and substituting the values, we get

$=\frac{1}{2}[(5 \times-3-2 \times-9)+(-9 \times-5-(-3 \times-3))+(-3 \times 2-(-5 \times 5))]$

$=\frac{1}{2}[(-15+18)+(45-9)+(-6+25)]$

$=\frac{1}{2}[3+36+19]$

$=\frac{1}{2} \times 58=29$ sq.units.

3. Find the area of the triangle whose vertices are $(10,-6),(2,5)$ and $(-1,3)$.

Ans: Area of $\triangle A B C=\frac{1}{2}\left[x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right]$

Substituting the values, we get

$A(10,-6), B(2,5)$ and $C(-1,3)$

Area of triangle $=\frac{1}{2}(49)(10(5-3)+2(3+6)-1(-6-5))$

$=\frac{1}{2}(49)(20+18+11)$

$=\frac{1}{2}(49)$

$=24.5 \mathrm{sq}$ units

Thus, the triangle is $=24.5 \mathrm{sq}$ units.

Practice Questions

Let's solve the following area of the triangle with the formula.

1. What is the area of the triangle whose vertices are X(3, 3), Y(3, 4), and Z(7, 0)?

Ans: 2 sq units

2. What is the area of the triangle whose vertices are A(4, 1), B(4, 5), and C(5, 6)?

Ans: 2 sq units

3. What is the area of the triangle whose vertices are A(1, 3), B(2, 2), and C(3, 5)?

Ans: 2 sq units

4. What is the area of the triangle whose vertices are X(1, 6), Y(4, 2), and Z(8, 5)?

Ans: 12.5 sq units

5. What is the area of the triangle whose vertices are A(4, 4), B(2, 2), and C(5, 5)?

Ans: 0 sq units

Summary

Generally speaking, an "area" is the area included within the perimeter of a flat object or figure. Measurements are made in square units, with square metres serving as the reference unit (m²). There are predefined formulas for the computation of area for squares, rectangles, circles, triangles, etc.

This article taught us the formulas for the area of triangles for various kinds of triangles, along with several sample issues. As triangles are isosceles and equilateral, they all have the same formula. The formula for the area of a triangle can be determined by using the Pythagorean theorem.