




Step-by-Step Guide: How to Add and Subtract Integers Efficiently
What do addition and subtraction mean in mathematics? The addition and subtraction of integers are two operations we perform on integers to increase or decrease their values. Integers include whole and negative numbers, such as 4, 5, 0, -9, -18, etc. Every number shown on a number line that does not have a fractional part is an integer. Let us learn more about adding and subtracting integers. In this article, we will learn the adding and subtracting integers rules to make the concept interesting, relatable, and easy to understand.
Integers on Number Line
Integers are a collective term for negative numbers, zero, and natural numbers. The right side of the number line is occupied by positive numbers, while negative numbers occupy the left side. The sign on the number denotes whether it is moving to the right of or away from zero.
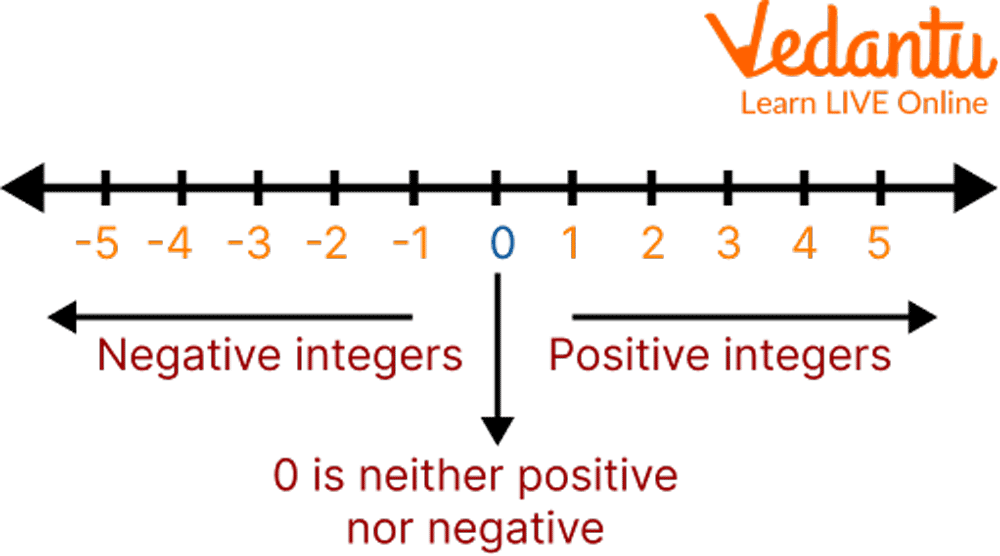
Integers on Number Line
For example, +3 means the number is to the right of 0, and -3 means it is to the left of 0. If a number has no sign, it is a positive integer.
Adding and Subtracting Integers on a Number Line
There is a specific rule for adding and subtracting positive and negative numbers from a number line:
We start with the first number and move to the right of the number line if we need to add a positive number to another positive number.
It should be noted that whenever we add a negative number, the number line shifts to the left.
We can convert the subtraction fact to an addition fact and change the sign of the subtraction if we need to subtract a positive number.
Now we will see how we are applying addition and subtraction rules for the integers one by one.
Rules to Add Integers
The following guidelines should be kept in mind when adding positive and negative integers:
Add the two integers when both have a positive sign.
When both integers have a negative sign, add them together and give the sum a (-) sign.
Subtract and use the sign of the larger number if the sign of the two numbers differs.
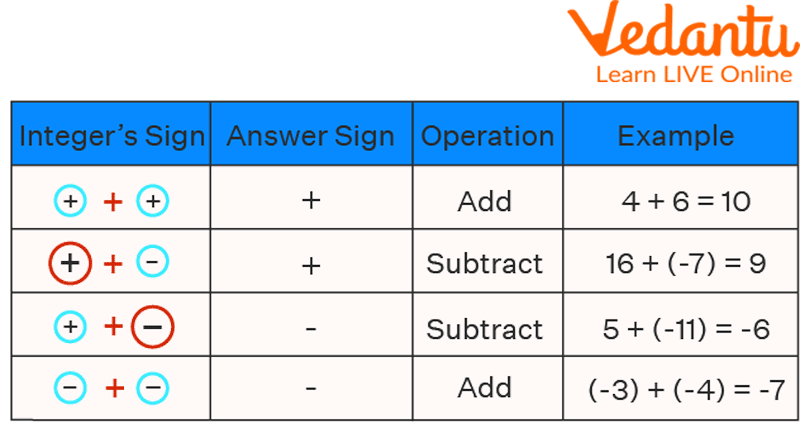
Rules to Add Integers
Rules to Subtract Integers
The following guidelines should be kept in mind to know how to subtract integers steps:
When subtracting two integers with the same sign, we first take the absolute values o
If the two numbers are, we add the common sign to the final result. A number's positive or absolute value is the number itself.
The sign of the subtrahend changes when two numbers with different signs are subtracted. The result will be positive if both integers change to the positive integer and negative if they change to the negative integer.
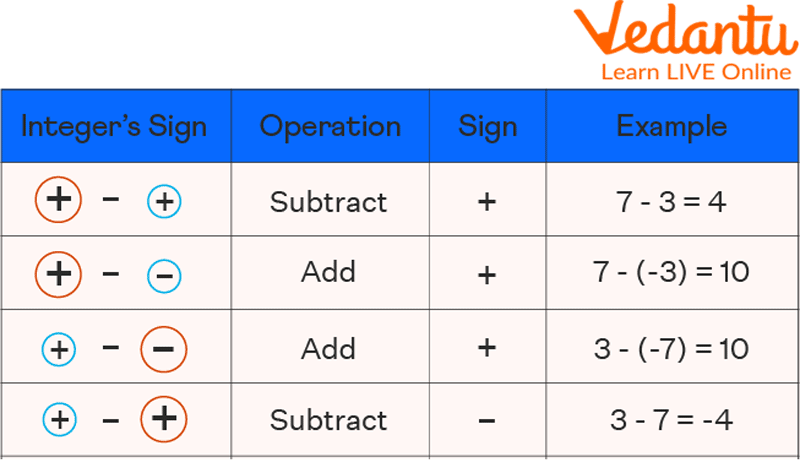
Rules to Subtract Integers
Solved Examples
Example 1: Evaluate 2 - 3 using a number line.
Solution: We will begin at +2 on a number line because it is our minuend. Since we are subtracting the value of 2 by 3, we must move the left three steps. We arrive at (-1), which is our answer.
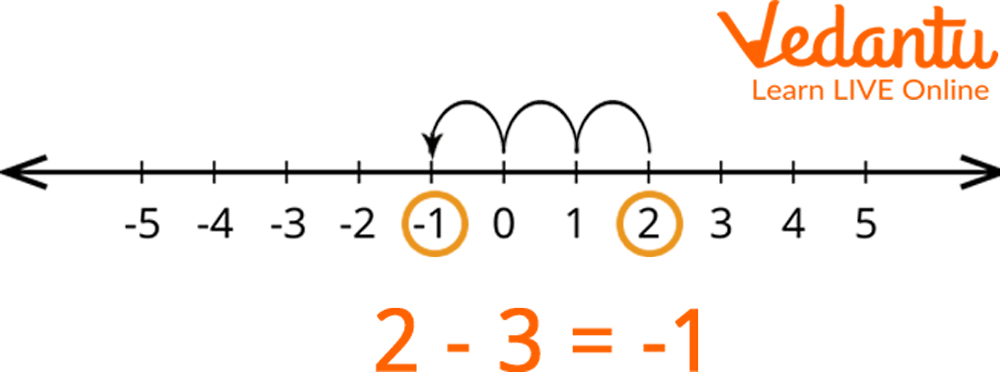
Number Line
Example 2: Add -16 and -23.
Solution: We have given that -16 and -23 are both negative numbers. The result of adding them together is a negative sum;
(-16)+(-23) = -16-23 = -39
Example 3: Subtract -46 from 88.
Solution: We reverse the sign of -46 and add it to 88 to subtract it from 88.
Therefore;
88- (-46) = 88 + 46 = 134
Example 4: Subtract -4 from -20.
Solution: We reverse the sign of -4 and add it to -20 to subtract it from -20.
Therefore;
-20 - (-4) = -20 + 4 = -16
Practice Problems
Q 1. Subtract: 544 – (-389) (Ans: 933)
Q 2. Subtract: 0 – (38) (Ans: -38)
Q 3. Addition: - 134 + (-18) (Ans: -152)
Q 4. Addition: 78 + (-22) (Ans: 56)
Summary
This article taught us the rules for adding and subtracting positive and negative numbers. A positive integer is carried out when you add two positive integers. A sum of negative integers is produced by adding two negative values. When subtracting two integers with the same sign, we first take the absolute values of the two numbers apart, and then we add the common sign to the final result. The sign of the subtrahend changes when two numbers with different signs are subtracted. At the end of the article, we have added the practice problem, so after going through the article, give it a try to practice questions too. This will help you to analyze your understanding of this topic.
FAQs on Adding and Subtracting Integers Made Easy
1. What is some application of integers?
Positive and negative numbers are used in the real world differently. Commonly, they are utilized to illustrate two opposing scenarios.
Temperature measurement is a typical real-world use for integers. Different temperatures are indicated by the negative, positive, and zero readings on the scale.
Integers are also used in bank credit and debit statements to represent the negative and positive values of the amount.
Integers are frequently used to indicate a location above or below sea level, the level of an elevator when it is above or below street level, as a bonus, a penalty in tests and games, and other things.
2. Are the rules for integer multiplication and division the same as those for addition and subtraction?
No. Integer multiplication and division follow different rules than addition and subtraction. The following are the fundamental rules for multiplying and dividing integers:
The result is positive when two positive integers are multiplied or divided.
The outcome is also positive if you multiply or divide two negative integers.
A negative number is produced when two numbers are multiplied or divided by their opposite signs.
3. What are the characteristics of integer addition?
Integers have the same addition properties as whole numbers listed below:
Closure Property: Any two integers added together produce an integer.
Commutative property: The sum of any two integers is the same regardless of the order in which they are added.
Associative Property: The grouping of the integers is irrelevant when computing the sum of three or more integers.
Additive Identity: If you add zero to any integer, the resulting answer will also be an integer. The number zero is the additive identity.
Additive Inverse: When an integer is added to an existing integer, the result is always 0. The two opposite integers are known as their additive inverses.























