Concise Mathematics Class 10 ICSE Solutions for Chapter 17 - Circle

Exercise-17A

Long Answer Type

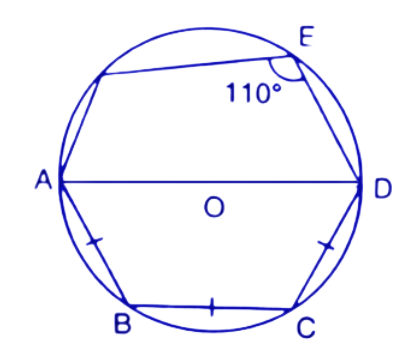
1. In the given figure O is the centre of the circle. ∠AOB and ∠OCB are ${{30}^{\circ }}$ and ${{40}^{\circ }}$ respectively. Find AOC. Show your steps of working.

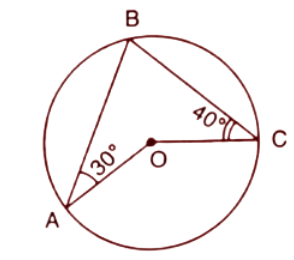
Ans: On joining the points A and C we get the triangles $\Delta AOC$ and $\Delta ABC.$

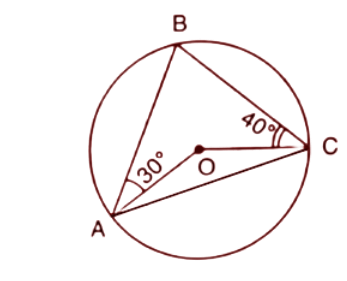
In $\Delta AOC$,

$\angle OAC=x~\text{and}~\angle OCA=x$ (∵ OA=OC (radius))

$\angle AOC={{180}^{\circ }}-\left( \angle OAC+\angle OCA \right)$

$\angle AOC={{180}^{\circ }}-2x$------(1)

 In $\Delta ABC$

∠BAC=${{30}^{\circ }}+x$

$\angle BCA={{40}^{\circ }}+x$

We know that in a triangle sum of angles is ${{180}^{\circ }}$

$\angle ABC={{180}^{\circ }}-\left( \angle BAC+\angle BCA \right)$

$={{180}^{\circ }}-\left( {{30}^{\circ }}+x+{{40}^{\circ }}+x \right)$

$={{110}^{\circ }}-2x$

Since the angle at centre is double the angle at the circumference subtended by the same chord.

$\angle AOC=2\angle ABC$

$\Rightarrow {{180}^{\circ }}-2x=2\left( {{110}^{\circ }}-2x \right)$

$\Rightarrow 4x-2x={{220}^{\circ }}-180$

$\Rightarrow 2x={{40}^{\circ }}$

$\Rightarrow x={{20}^{\circ }}$

So from eq.1 the value of $\angle AOC$ is:

$\angle AOC={{180}^{\circ }}-2x={{180}^{\circ }}-{{40}^{\circ }}={{140}^{\circ }}$

2. In the given figure, $\angle BAD={{65}^{\circ }}$, $\angle ABD={{70}^{\circ }},~\angle BDC={{45}^{\circ }}$

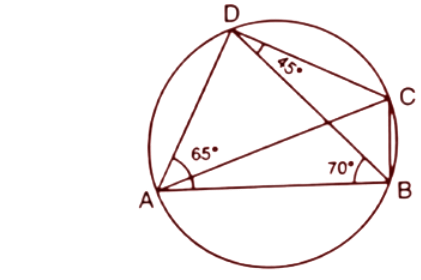
(i). Prove that AC is diameter of the circle

Ans:  In $\Delta ADB$

$\angle ADB+\angle DAB+\angle ABD={{180}^{\circ }}$

$\Rightarrow \angle ADB+{{65}^{\circ }}+{{70}^{\circ }}={{180}^{\circ }}$

$\Rightarrow \angle ADB={{180}^{\circ }}-{{135}^{\circ }}={{45}^{\circ }}$

Since, $\angle ADC=\angle ADB+\angle BDC$

$\angle ADC={{45}^{\circ }}+{{45}^{\circ }}={{90}^{\circ }}$

$\angle ADC={{90}^{\circ }}$

Hence the triangle $\Delta ADC$is a right angled triangle and we know that when a triangle is inserted in a circle in such a way that the triangle is a right triangle then one of the sides of the triangle is the diameter of the circle, Hence AC is the diameter of the triangle.

(ii). Find $\angle ACB$ 

Ans: We know that angles in the same segments of circle are equal. 

$\angle ACB=\angle ADB$ (∵$\angle ADB={{45}^{\circ }}$)

Hence, $\angle ACB={{45}^{\circ }}$

3. Given O is the centre of the circle and $AOB={{70}^{\circ }}$, Calculate the value of :

(i).$~\angle OCA$

Ans: We know that the angle at the centre is double 

the angle at the circumference subtended by the same chord.

$\angle AOB=2\angle ACB$

So the value of $\angle ACB=\dfrac{{{70}^{\circ }}}{2}={{35}^{\circ }}$

ACB and OAC are b/w the same line segments.

Hence $\angle ACB=OCA={{35}^{\circ }}$------(1)

(ii). $\angle OAC$

Ans: ∵ OA=OC (radii of circle)

Thus the values

 $\angle OCA=\angle OAC={{35}^{\circ }}$[from eq.1]

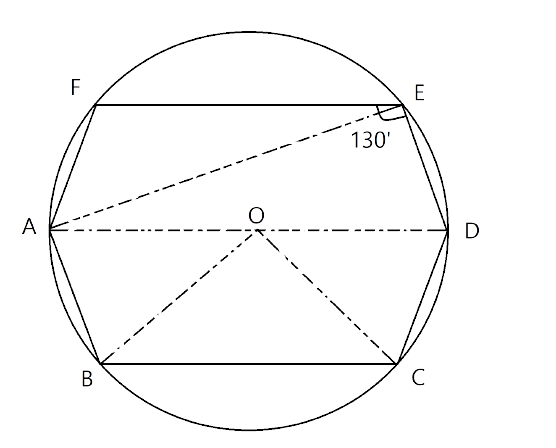
4. In each of the following figures, O is the centre of the circle. Find the values of a,b and c.

(i).

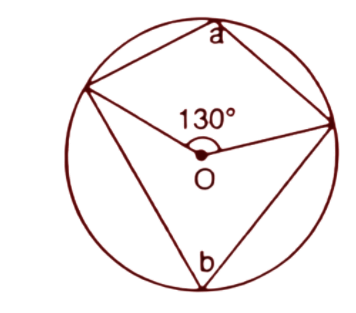
Ans: The angle at the centre is double the angle at the circumference subtended by the same chord.

$2b={{130}^{\circ }}$

$\Rightarrow b=\dfrac{1}{2}\times {{130}^{\circ }}={{65}^{\circ }}$

By the theorem, the opposite angles of a cyclic quadrilateral are supplementary.

Hence $a+b={{180}^{\circ }}$

$\Rightarrow a+{{65}^{\circ }}={{180}^{\circ }}$

$\Rightarrow a={{180}^{\circ }}-{{65}^{\circ }}={{115}^{\circ }}$

Thus the values of a and b are respectively ${{115}^{\circ }}~\And ~{{65}^{\circ }}~$.

(ii)

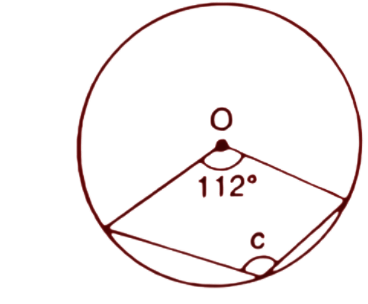
Ans: Given, central angle =${{112}^{\circ }}$

Reflex angle of  ${{112}^{\circ }}$= ${{360}^{\circ }}-{{112}^{\circ }}={{248}^{\circ }}$

We know that the angle at the centre is double the angle at the circumference by the same arc.

Hence, $2c=$ Reflex angle of ${{112}^{\circ }}$

$2c={{248}^{\circ }}$

$\Rightarrow c=\dfrac{{{248}^{\circ }}}{2}={{124}^{\circ }}$

Thus the value of angle c is ${{124}^{\circ }}$.

5. In each of the following figures, O is the centre of the circle. Find the values of a,b,c and d.

(i).

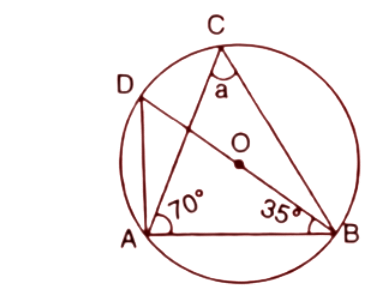
Ans: Here O is the centre of the circle and BD is the Diameter of the given circle and side of the triangle ABD as well.

We know the angle at the semicircle is a right angle triangle. Hence $\angle DAB={{90}^{\circ }}$

The sum of angles in a triangle is ${{180}^{\circ }}$

$\angle DAB+\angle ADB+\angle DBA={{180}^{\circ }}$

$\Rightarrow {{90}^{\circ }}+\angle ADB+{{35}^{\circ }}={{180}^{\circ }}$  (Given  $\angle DBA={{35}^{\circ }}$)

$\Rightarrow \angle ADB={{180}^{\circ }}-{{125}^{\circ }}={{55}^{\circ }}$

We know that angles in the same segment of circle are always equal.

$\angle ADB=\angle ACB$

$a={{55}^{\circ }}$ ($\angle ADB={{55}^{\circ }}$ and $\angle ACB=a$)

Thus the value of a is ${{55}^{\circ }}$.

(ii).

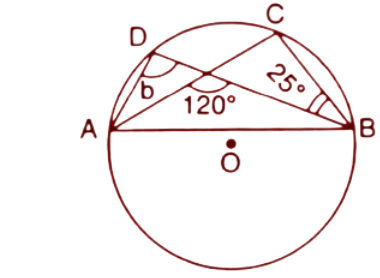
Ans: In a circle angles at the circumference subtended by the same chord are always equal. Angles $\angle DAC$ and $\angle DBC$ are subtended by the chord DC.

$\angle DAC=\angle DBC={{25}^{\circ }}$

By the exterior angle property the exterior angle in a triangle is equal to the sum of opposite interior angles.

$b+{{25}^{\circ }}={{120}^{\circ }}$

$\Rightarrow b={{95}^{\circ }}$

Thus the value of $b$ is ${{95}^{\circ }}$

(iii).

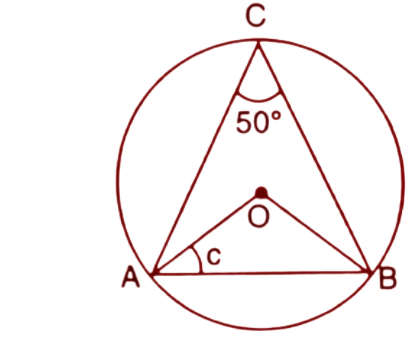
Ans: We know that the angle at the centre is double the angle at the circumference subtended by the same chord.

$\angle AOB=2.~\angle ACB$

$\Rightarrow \angle AOB=2\times {{50}^{\circ }}={{100}^{\circ }}$

Also, OA=OB (Radii of the circle)

Hence the $\Delta AOB$ is an isosceles triangle.

So, $\angle OAB=\angle OBA=c$

The sum of angles in a triangle is always ${{180}^{\circ }}$

$\angle OAB+\angle AOB+\angle OBA={{180}^{\circ }}$

$\Rightarrow c+\angle AOB+c={{180}^{\circ }}$

$\Rightarrow 2c={{180}^{\circ }}-{{100}^{\circ }}^{{}}$

$\Rightarrow c=\dfrac{{{80}^{\circ }}}{2}={{40}^{\circ }}$

Thus the value of c is ${{40}^{\circ }}$.

(IV).

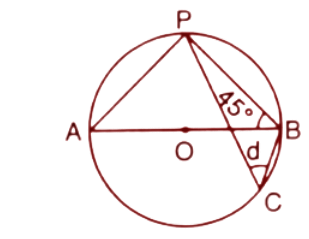
Ans: Given, angle $\angle PBA={{45}^{\circ }}$

AB is the diameter of the circle hence $\Delta APB$ is a right angle triangle and we know that angle in the semicircle is a right triangle. So ($\angle APB={{90}^{\circ }}$).

The sum of angles in a triangle is always ${{180}^{\circ }}$

$\angle PAB+\angle PBA+\angle APB={{180}^{\circ }}$

$\Rightarrow \angle PAB+{{45}^{\circ }}+{{90}^{\circ }}={{180}^{\circ }}$

$\Rightarrow \angle PAB={{180}^{\circ }}-{{135}^{\circ }}$

$\Rightarrow \angle PAB={{45}^{\circ }}$---------(1)

Now, the angles subtended by the same chord are equal. Here the angels $\angle PAB$ and $\angle PCB$ subtended by the chord PB. 

Hence $\angle PAB=\angle PCB$

From eq. 1

$\angle PCB=\angle PAB={{45}^{\circ }}$

$d={{45}^{\circ }}$   ($\because \angle PCB$=d)

Thus the value of angle d is ${{45}^{\circ }}$.

6. In the figure, AB is the common chord of the two circles. If AC and AD are diameters; prove that D,B and C are in a straight line. ${{O}_{1}}$and ${{O}_{2}}$ are the centres of two circles.

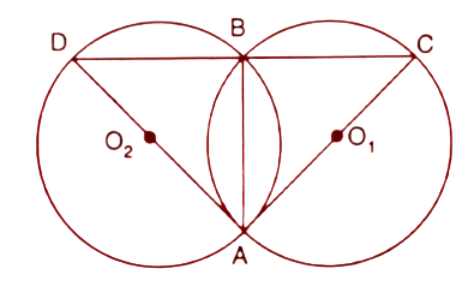
Ans:

Given, ${{O}_{1}}$and ${{O}_{2}}$ are the centres of the circles.

Here AD and AC are the diameter of the circles. So the angles $\angle DBA$ and $\angle ABC$are in the semicircles and we know that the angle in the semicircle is a right angle.

Hence, $\angle DBA=\angle CBA={{90}^{\circ }}$

On Adding both the angles 

$\angle DBA+\angle CBA={{90}^{\circ }}+{{90}^{\circ }}={{180}^{\circ }}$

Thus D,B and C form a straight line.

7. In the figure, given below, find:

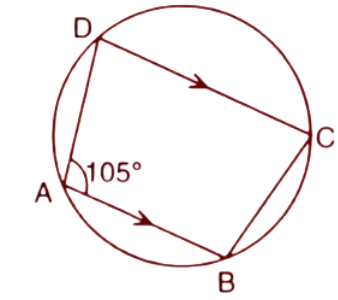
$\left( i \right)\angle BCD,$

(ii). $\angle ADC,$

(iii). $\angle ABC$.

Show steps of your working. 

(i). $\angle BCD$

Ans: In a cyclic quadrilateral the sum of 

opposite angles are always ${{180}^{\circ }}$.

$\angle DAB+\angle BCD={{180}^{\circ }}$

Given, $\angle DAB={{105}^{\circ }}$ 

Now, ${{105}^{\circ }}+\angle BCD={{180}^{\circ }}$

$\Rightarrow \angle BCD={{180}^{\circ }}-{{105}^{\circ }}$

$\Rightarrow \angle BCD={{75}^{\circ }}$

Thus the value of $\angle BCD$ is ${{75}^{\circ }}$.

(ii). $\angle ADC$

Ans: From the figure, $AB||CD$, and we know that the sum of interior angles on the same side of parallel lines is ${{180}^{\circ }}$.

$\angle BAD+\angle ADC={{180}^{\circ }}$

$\Rightarrow \angle ADC={{180}^{\circ }}-{{105}^{\circ }}={{75}^{\circ }}$

Thus the value of $\angle ABC$is ${{75}^{\circ }}$.

(iii). $\angle ABC$

Ans: In a cyclic quadrilateral the sum of opposite angles is always ${{180}^{\circ }}$.

$\angle ADC+\angle ABC={{180}^{\circ }}$

$\Rightarrow \angle ABC={{180}^{\circ }}-{{75}^{\circ }}={{105}^{\circ }}$

Thus the value of $\angle ABC$ is ${{105}^{\circ }}$.

8. In the given figure, O is the centre of the circle. If $\angle AOB={{140}^{\circ }}$ and $\angle OAC={{50}^{\circ }}$, find:

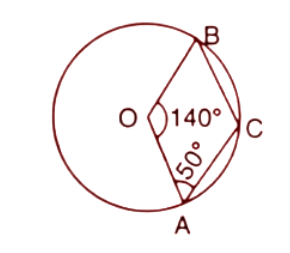
(i). $\angle ACB$

Ans: Given, $\angle AOB={{140}^{\circ }}$and $\angle OAC={{50}^{\circ }}$

Reflex angle of $\angle AOB$ is ${{360}^{\circ }}-{{140}^{\circ }}={{220}^{\circ }}$

We know that the angle at the centre is double the angle at the circumference.

Reflex angle of $\angle AOB~=2\angle ACB$

$\Rightarrow \angle ACB=\dfrac{1}{2}\times \text{Reflex angle of} \angle AOB~$

$\Rightarrow \angle ACB=\dfrac{1}{2}\times {{220}^{\circ }}={{110}^{\circ }}^{{}}~$

Thus the angle $\angle ACB$ is ${{110}^{\circ }}$.

(ii).$\angle OAB,$

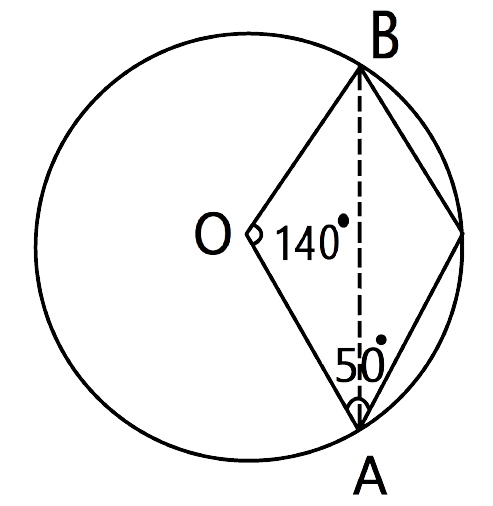
Ans: Since OA=OB (Radii of circle)

Hence $\angle OAB=\angle OBA$---------(1)

And we know that the sum of angles of a triangle 

is always ${{180}^{\circ }}.$

So, $\angle OAB+\angle AOB+\angle OBA={{180}^{\circ }}$

From eq. 1

$2\angle OBA={{180}^{\circ }}-{{140}^{\circ }}={{40}^{\circ }}$

$\Rightarrow \angle OBA={{20}^{\circ }}$

∵$\angle OAB=\angle OBA$

Só, $\angle OAB=\angle OBA={{20}^{\circ }}$

Thus the value of $\angle OAB$ is ${{20}^{\circ }}$.

(iii).$\angle OBC$

Ans: In $\Delta ACB$

$\angle ACB+\angle CBA+\angle CAB={{180}^{\circ }}$

$\because \angle CAB={{50}^{\circ }}-\angle OAB={{50}^{\circ }}-{{20}^{\circ }}={{30}^{\circ }}$

$\Rightarrow {{110}^{\circ }}+\angle CBA+{{30}^{\circ }}={{180}^{\circ }}$

$\Rightarrow \angle CBA={{180}^{\circ }}-{{140}^{\circ }}={{40}^{\circ }}$------(2)

Since, $\angle OBC=\angle OBA+\angle CBA={{40}^{\circ }}+{{20}^{\circ }}={{60}^{\circ }}$

(iv).$\angle CBA,$

Ans: In $\Delta ABC,$

From eq. 2 the value of $\angle CBA$ is ${{40}^{\circ }}$.

9. Calculate: 

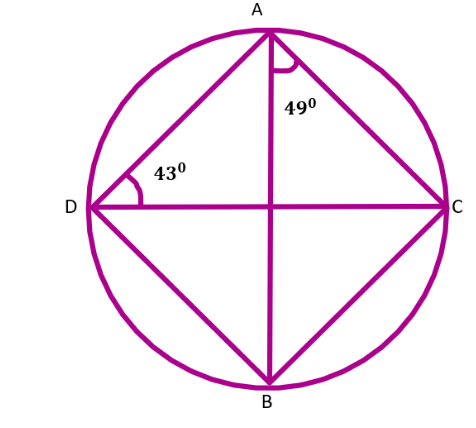
(i).$\angle CDB,$

Ans: We know that the angle subtended by the same chord on the circle is equal.

Here in the given circle $\angle CDB$ and $\angle BAC$ are subtended by the chord BC.

Hence $\angle CDB=\angle BAC$

$\because \angle BAC={{49}^{\circ }}$

So, $\angle CDB={{49}^{\circ }}$

Thus the value of $\angle CDB$ is ${{49}^{\circ }}$.

(ii).$\angle ABC,$

Ans: The angle subtended by the same chord on the circle is equal.

Here in the given circle $\angle ADC$ and $\angle ABC$ are subtended by the chord AC.

Hence $\angle ADC=\angle ABC$

$\because \angle ADC={{43}^{\circ }}$

So, $\angle ABC={{43}^{\circ }}$

Thus the value of $\angle ABC$ is ${{43}^{\circ }}$.

(iii).$\angle ACB$

Ans: By the angle sum property the sum of angles in a triangle is ${{180}^{\circ }}$.

In $\Delta ACB$,

$\angle ACB+\angle BAC+\angle ABC={{180}^{\circ }}$

$\Rightarrow \angle ACB+{{49}^{\circ }}+{{43}^{\circ }}={{180}^{\circ }}$

$\Rightarrow \angle ACB={{180}^{\circ }}-{{92}^{\circ }}={{88}^{\circ }}$

Thus the value of $\angle ACB$ is ${{88}^{\circ }}$.

10. In the figure, given below, ABCD is a cyclic quadrilateral in which $\angle BAD={{75}^{\circ }}$; $\angle ABD={{58}^{\circ }}$ and $\angle ADC={{77}^{\circ }}$. Find:

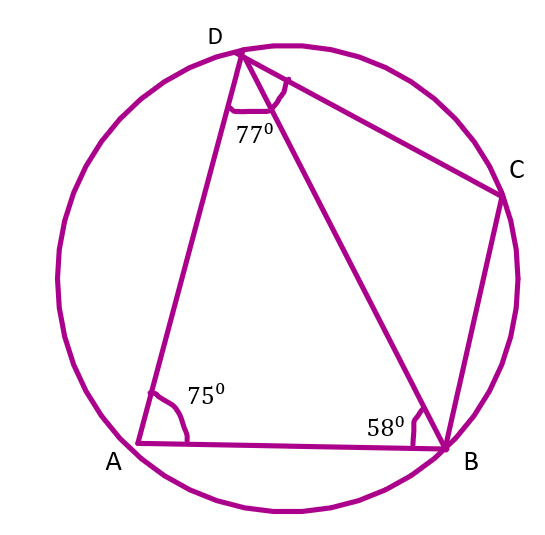
(i). $\angle BDC,$

Ans: By the angle sum property we know that the sum 

of all interior angles in a triangle is ${{180}^{\circ }}$.

In $\Delta ADB$

$\angle ADB+\angle ABD+\angle BAD={{180}^{\circ }}$

$\Rightarrow \angle ADB+{{58}^{\circ }}+{{75}^{\circ }}={{180}^{\circ }}$

$\Rightarrow \angle ADB={{180}^{\circ }}-{{133}^{\circ }}={{47}^{\circ }}$

$\because \angle ADC=\angle ADB+\angle BDC$

$\Rightarrow {{77}^{\circ }}={{47}^{\circ }}+\angle BDC$  (Given $\angle ADC={{77}^{\circ }}^{{}}$)

$\angle BDC={{77}^{\circ }}-{{47}^{\circ }}={{30}^{\circ }}$

Thus the value of $\angle BDC$ is ${{30}^{\circ }}$.

(ii). $\angle BCD,$

Ans: By the property of cyclic quadrilaterals, the opposite angles of a cyclic quadrilateral are supplementary. Here $\angle BAD$ and $\angle BCD$ are opposite angles. 

So, $\angle BAD+\angle BCD={{180}^{\circ }}$

$\Rightarrow {{75}^{\circ }}+\angle BCD={{180}^{\circ }}$ (From the figure, $\angle BAD={{75}^{\circ }}$)

$\Rightarrow \angle BCD={{180}^{\circ }}-{{75}^{\circ }}={{105}^{\circ }}$

Thus the value of $\angle BCD$ is ${{105}^{\circ }}$.

(iii). $\angle BCA$

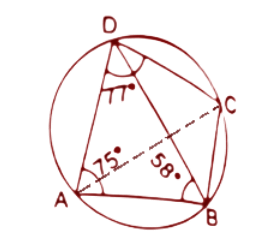
Ans: Angles subtended by the same chord in the same segment of a circle are always equal. Here the angels  $\angle BCA$ and $\angle ADB$ are subtended by the chord AB.

Hence, $\angle BCA=\angle ADB$ 

$\because \angle ADB={{47}^{\circ }}$

Then, $\angle BCA={{47}^{\circ }}$

Thus the value of $\angle BCA$ is ${{47}^{\circ }}$.

11. In the following figure, O is the centre of the circle and $\Delta ABC$ is equilateral.

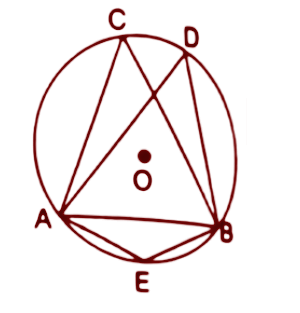
Find: 

(i). $\angle ADB$

Ans: Given that $\Delta ABC$ is an equilateral triangle.

So all the angles will be equal.

So, In$\Delta ABC$

$\angle ACB=\angle ABC=\angle CAB$

$\Rightarrow \angle ACB+\angle ABC+\angle CAB={{180}^{\circ }}$

$\Rightarrow 3\angle ACB={{180}^{\circ }}$

$\Rightarrow \angle ACB={{60}^{\circ }}$

We know that angles subtended by the same chord are always equal. Here $\angle ACB$ and $\angle ADB$ are subtended by the chord AB.

Hence, $\angle ADB=\angle ACB={{60}^{\circ }}$

Thus the value of $\angle ADB$ is ${{60}^{\circ }}$.

(ii).$\angle AEB$

Ans: Join OA and OB.

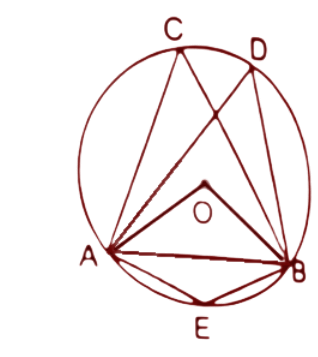
The angle at the centre is double the angle at the circumference of the circle by the same chord.

$\angle AOB=2\angle ACB$

$\because \angle ACB={{60}^{\circ }}$

∴$\angle AOB=2\times {{60}^{\circ }}={{120}^{\circ }}$

Here the reflex angle of $\angle AOB$ will be double the angle $\angle AEB$ as these are subtended by the same chord AB.

Hence, Reflex angle of $\angle AOB=2\angle AEB$

$\Rightarrow \angle AEB=\dfrac{1}{2}\times Reflex~angle~of~\angle AOB~$

$\Rightarrow \angle AEB=\dfrac{1}{2}\times \left( {{360}^{\circ }}-{{120}^{\circ }} \right)=\dfrac{1}{2}\times {{240}^{\circ }}={{120}^{\circ }}$

Thus the value of $\angle AEB$ is ${{120}^{\circ }}$.

12. Given: $\angle CAB={{75}^{\circ }}$ and $\angle CBA={{50}^{\circ }}.$ Find the value of $\angle DAB+\angle ABD.$

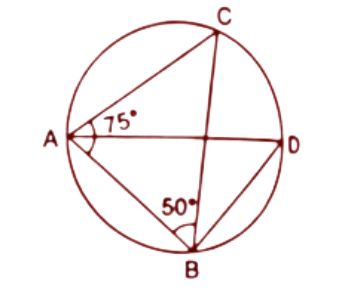
Ans: By the angle sum property the sum of angles in a triangle is always ${{180}^{\circ }}.$

In $\Delta ABC$,

$\angle CAB+\angle ABC+\angle ACB={{180}^{\circ }}$

$\Rightarrow {{75}^{\circ }}+{{50}^{\circ }}+\angle ACB={{180}^{\circ }}$[Given $\angle CAB={{75}^{\circ }}~\And \angle CBA={{50}^{\circ }}]$

$\Rightarrow \angle ACB={{180}^{\circ }}-{{125}^{\circ }}={{55}^{\circ }}$

The angle subtended by the same chord is always equal.

Here $\angle ACB$and $\angle ADB$ are subtended by the chord AB.

Hence, $\angle ADB=\angle ACB={{55}^{\circ }}$

In $\Delta ADB$,

$\angle DAB+\angle ABD+\angle ADB={{180}^{\circ }}$

$\Rightarrow \angle DAB+\angle ABD={{180}^{\circ }}-{{55}^{\circ }}={{125}^{\circ }}$

Therefore the value of $\angle DAB+\angle ABD$ is ${{125}^{\circ }}$.

13. ABCD is a cyclic quadrilateral in a circle with centre O. If $\angle ADC={{130}^{\circ }},$ find $\angle BAC.$

Ans: We know that the angle made in a semicircle is the right angle.

Here AB is a diameter and $\angle ACB$ will be the right angle.

So,  $\angle ACB={{90}^{\circ }}$

In a cyclic quadrilateral, opposite angles are supplementary.

So, $\angle ADC+\angle ABC={{180}^{\circ }}$

$\Rightarrow \angle ABC={{180}^{\circ }}-{{130}^{\circ }}={{50}^{\circ }}$

Now, By using angle sum property in $\Delta ABC$

$\angle ABC+\angle BAC+\angle ACB={{180}^{\circ }}$

$\Rightarrow {{50}^{\circ }}+\angle BAC+{{90}^{\circ }}={{180}^{\circ }}$ ($\angle ABC={{50}^{\circ }},\angle ABC={{90}^{\circ }}$)

$\Rightarrow \angle BAC={{180}^{\circ }}-{{140}^{\circ }}={{40}^{\circ }}$

Thus the value of angle $\angle BAC$is ${{40}^{\circ }}$.

14. In the figure, given alongside, AOB is a diameter of the circle and $\angle AOC={{110}^{\circ }},$ find $\angle BDC$.

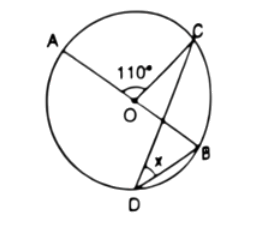
Ans: First we join points A and D.

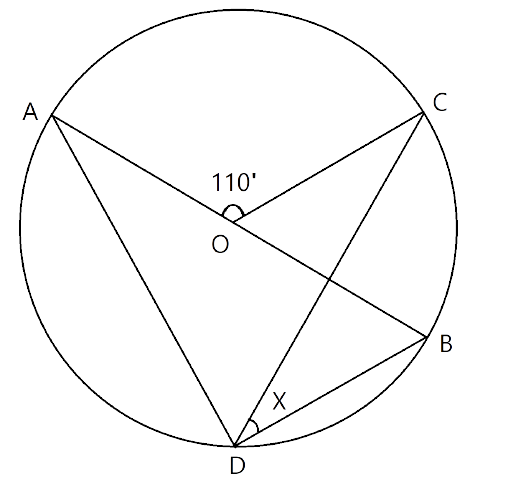
In a circle the angle at the centre is double the angle at the circumference subtended by the same chord.

$\angle AOC=2\angle ADC$

$\Rightarrow \angle ADC=\dfrac{1}{2}\times {{110}^{\circ }}={{55}^{\circ }}$

Now, Angle made in the semicircle is a right angle. Here angle $\angle ADB$ is the angle subtended by the diameter AB so this is the angle made in semicircle. Hence $\angle ADB$ is the right angle.

Therefore, $\angle ADB={{90}^{\circ }}$

Since, $\angle ADB=\angle ADC+\angle BDC$

$\Rightarrow {{90}^{\circ }}={{55}^{\circ }}+\angle BDC$

$\Rightarrow \angle BDC={{35}^{\circ }}$

Thus the value of angle $\angle BDC$ is ${{35}^{\circ }}$.

15. In the following figure, O is the centre of the circle, $\angle AOB={{60}^{\circ }}$ and $\angle BDC={{100}^{\circ }}$. Find $\angle OBC$.

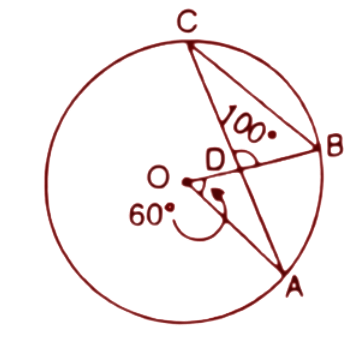
Ans: In a circle the angle at the centre is double the angle at the circumference by the same chord. Here angle $\angle AOB$ is the angle at centre and $\angle ACB$ at circumference subtended by the same arc AB. 

Hence, $\angle AOB=2\angle ACB$

$\Rightarrow \angle ACB=\dfrac{1}{2}\times \angle AOB=\dfrac{1}{2}\times {{60}^{\circ }}={{30}^{\circ }}$

In $\Delta BOC$ , By using the angle sum property

$\Rightarrow \angle BOC+\angle OBC+\angle OCB={{180}^{\circ }}$

$\Rightarrow {{100}^{\circ }}+\angle OBC+{{30}^{\circ }}={{180}^{\circ }}$  (∵ $\angle OCB=\angle ACB$)

$\Rightarrow \angle OBC={{180}^{\circ }}-{{130}^{\circ }}={{50}^{\circ }}$

Thus the value of $\angle OBC$ is ${{50}^{\circ }}$.

16. In cyclic quadrilateral ABCD, $\angle DAC={{27}^{\circ }};\angle DBA={{50}^{\circ }}$ and $\angle ADB={{33}^{\circ }}.$ Calculate:

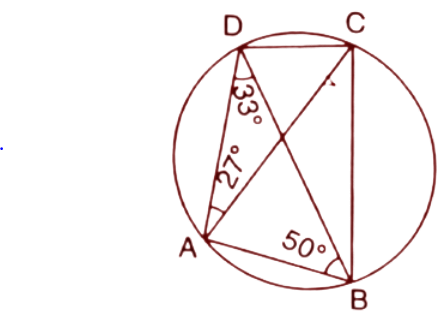
(i). $\angle DBC,$

Ans:  In a circle, Angles at the circumference subtended by the same chord are equal. Here the $\angle DAC$ and $\angle DBC$ are subtended by the chord DC.

Hence $\angle DAC=\angle DBC$

$\Rightarrow \angle DBC={{27}^{\circ }}$  (∵$\angle DAC={{27}^{\circ }}$)

So the value of $\angle DBC$ is ${{27}^{\circ }}$

(ii). $\angle DCB,$

Ans: In a circle, Angles at the circumference subtended by the same chord are equal.

$\angle DCA=\angle DBA={{50}^{\circ }}-----\left( 1 \right)$(Subtended by the same chord AD)

$\angle ACB=\angle ADB={{33}^{\circ }}------\left( 2 \right)$  (Subtended by the same chord AB)

From the figure, 

$\angle DCB=\angle DCA+\angle ACB$

From eq. 1 and eq.2 $\angle DCA={{50}^{\circ }}\And \angle ACB={{33}^{\circ }}$

$\angle DCB={{50}^{\circ }}+{{33}^{\circ }}={{83}^{\circ }}^{{}}$

So the value of $\angle DCB$is ${{83}^{\circ }}^{{}}$.

(iii). $\angle CAB.$

Ans: In a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$.

$\angle DCB+\angle DAB={{180}^{\circ }}$

$\Rightarrow \angle DAB={{180}^{\circ }}-83={{97}^{\circ }}$

$\Rightarrow \angle DAC+\angle CAB={{97}^{\circ }}$  (∵$\angle DAB=\angle DAC+\angle CAB$)

$\Rightarrow \angle CAB={{97}^{\circ }}-{{27}^{\circ }}={{70}^{\circ }}$

Thus the value of $\angle CAB$ is ${{70}^{\circ }}$.

17. In the figure given alongside, AB and CD are straight lines through the centre O of a circle. If $\angle AOC={{80}^{\circ }}$ and $\angle CDE={{40}^{\circ }},$ find the number of degrees in:

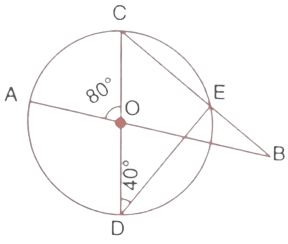
(i). $\angle DCE$

Ans: The angle made in a semicircle is the right angle. Here CD is the diameter so the angle $\angle CED$ will be at the right angle. Hence $\angle CED={{90}^{\circ }}$.

Now, By using the angle sum property in $\Delta CDE$.

$\angle CED+\angle CDE+\angle DCE={{180}^{\circ }}$

$\Rightarrow {{90}^{\circ }}+{{40}^{\circ }}+\angle DCE={{180}^{\circ }}$

$\Rightarrow \angle DCE={{180}^{\circ }}-{{130}^{\circ }}={{50}^{\circ }}$

Thus the value of $\angle DCE$ is ${{50}^{\circ }}$.

(ii). $\angle ABC$

Ans: We know that In a triangle the exterior angle is equal to the sum of a pair of opposite angles.

In $\Delta BOC$,

$\angle AOC$ is the exterior angle.

$\angle AOC=\angle OCB+\angle OBC$

$\Rightarrow {{80}^{\circ }}={{50}^{\circ }}+\angle OBC$

$\Rightarrow \angle OBC={{30}^{\circ }}$

Since, $\angle ABC=\angle OBC={{30}^{\circ }}$

Thus the value of $\angle ABC$ is ${{30}^{\circ }}$.

18. In the given figure, AC is the diameter of a circle,whose centre is O. A circle is described on AO as diameter. AE, is a chord of the larger circle, intersects the smaller circle at B. Prove that AB=BE.

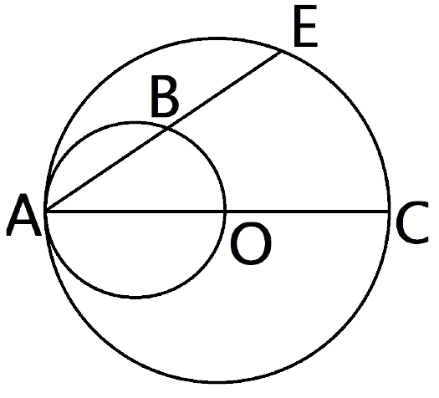
Ans: First we join points B and O.

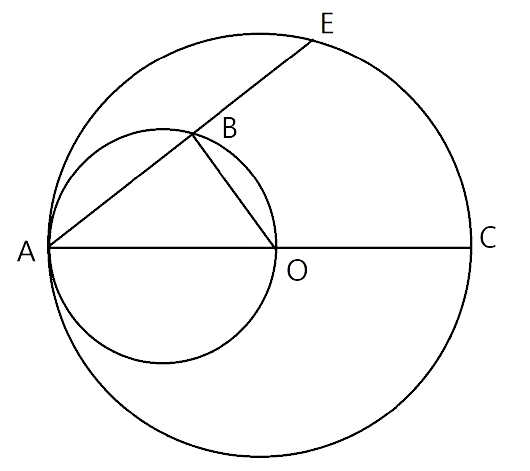
Now In triangle $\Delta ABO$ The side OA is also the diameter of a smaller circle. Hence the $\Delta ABO$ is a right angle triangle. And the angle $\angle ABO={{90}^{\circ }}$.

So, $AB\bot OB\Rightarrow AE\bot OB$

And we know that if we draw the perpendicular on the chord from the centre then the perpendicular bisects the chord.

Hence, AB=BE.

19. (a). In the following figure,

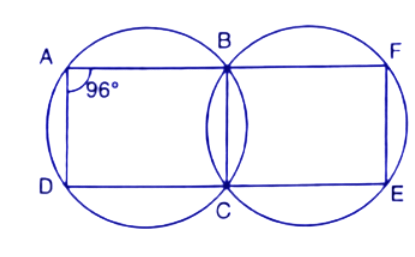
(i). If $\angle BAD={{96}^{\circ }}$, find$\angle BCD$and $\angle BFE.$

Ans: ABCD is a cyclic quadrilateral and we know that the sum of opposite angles in a cyclic quadrilateral is ${{180}^{\circ }}$.

So, $\angle BAD+\angle BCD={{180}^{\circ }}$

$\Rightarrow {{96}^{\circ }}+\angle BCD={{180}^{\circ }}$

$\Rightarrow \angle BCD={{180}^{\circ }}-{{96}^{\circ }}={{84}^{\circ }}$

Now,

$\angle BCD+\angle BCE={{180}^{\circ }}$

$\Rightarrow \angle BCE={{180}^{\circ }}-{{84}^{\circ }}={{96}^{\circ }}$

Here BCEF is also a cyclic quadrilateral.

So, $\angle BCE+\angle BFE={{180}^{\circ }}$

$\Rightarrow \angle BFE={{180}^{\circ }}-{{96}^{\circ }}={{84}^{\circ }}$

Thus the value of $\angle BCD$ and $\angle BFE$ are respectively ${{96}^{\circ }}$ and ${{84}^{\circ }}$.

(ii). Prove that AD is parallel to FE.

Ans: ADEF is a cyclic quadrilateral 

Here $\angle BAD+\angle BFE={{96}^{\circ }}+{{84}^{\circ }}={{180}^{\circ }}$

$\Rightarrow \angle BAD+\angle BFE={{180}^{\circ }}$

Here $\angle BAD$ and $\angle BFE$ are co-interior angles on the same side of a pair of lines AD and EF. 

By converse of the co-interior angle theorem, if a transversal line intersects two lines in such a way that the sum of a pair of co-interior angles is ${{180}^{\circ }}$then the lines are parallel lines.

Hence, AD||EF.

(b). ABCD is a parallelogram. A circle through vertices A and B meets side BC at point P and side AD at point Q. Show that quadrilateral PCDQ is cyclic.

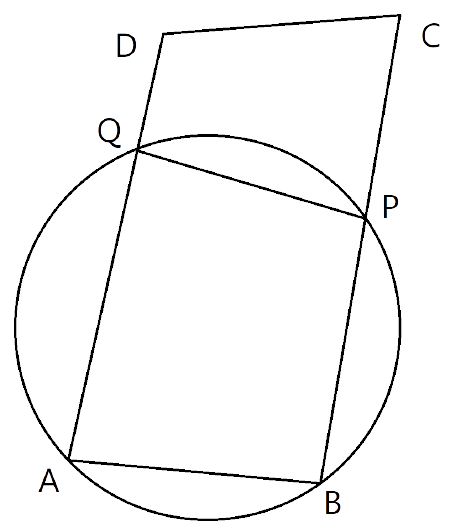
Ans: ABPQ is cyclic quadrilateral.

$\angle PCD=\angle BAQ$-----(1) (opposite angles of parallelogram)

$\angle BAQ=\angle QPC$-------(2) (exterior angle of cyclic Quadrilateral)

From eq.(1)&(2)

$\angle PCD=\angle QPC$------(3)

Here ABCD is a parallelogram, So the sum of the co-interior angles on the same side is ${{180}^{\circ }}$.

Hence, $\angle QDC+\angle PCD={{180}^{\circ }}$

From eq.(3) $\angle PCD=\angle QPC$

$\Rightarrow \angle QDC+\angle QPC={{180}^{\circ }}$

We know that if the sum of opposite angles of a quadrilateral is ${{180}^{\circ }}$ then the quadrilateral is a cyclic quadrilateral. Here $\angle QDC~\And ~\angle QPC$ are the opposite angles of quadrilateral PCDQ and we got the sum as ${{180}^{\circ }}$. 

Therefore PCDQ is a cyclic quadrilateral.

20. Prove that:

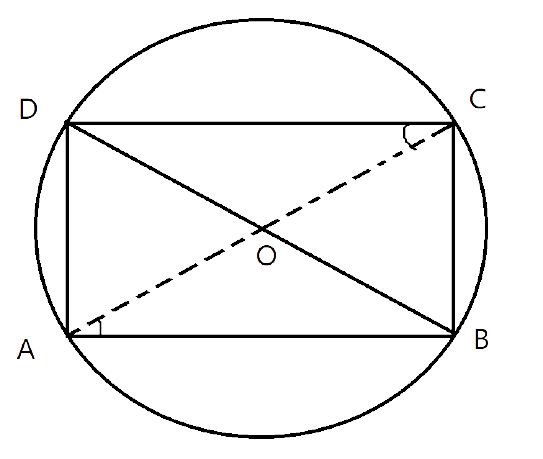
(i)The parallelogram inside the circle is a rectangle.

Ans: 

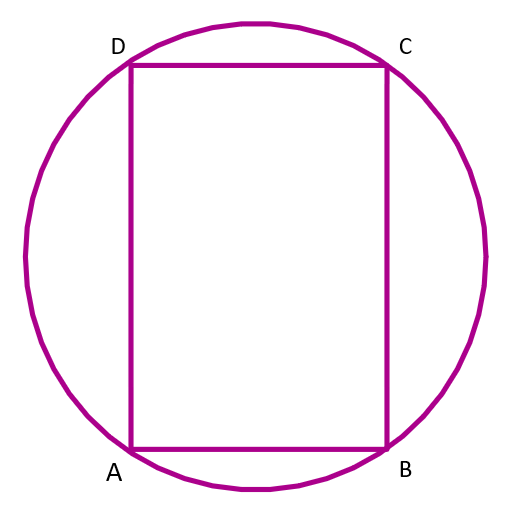
Let ABCD is a parallelogram inside the circle.

In parallelogram, Opposite sides and opposite angles are equal.

Therefore, AB=CD and $\angle BAD=\angle BCD$

Since, ABCD is also a cyclic quadrilateral.

So, $\angle BAD+\angle BCD={{180}^{\circ }}$

$\Rightarrow 2\angle BAD={{180}^{\circ }}$

$\Rightarrow \angle BAD={{90}^{\circ }}$

Therefore, $\angle BAD=\angle BCD={{90}^{\circ }}$

Similarly, The other two angles will be right angles and the other pair of opposite sides are equal. Hence all the respective sides are equal. 

$\angle BAD=\angle BCD=\angle ABC=\angle ADC={{90}^{\circ }}$

AB=CD and  BC=AD

So the parallelogram ABCD is a rectangle.

(ii). The rhombus, inscribed in a circle, is a square.

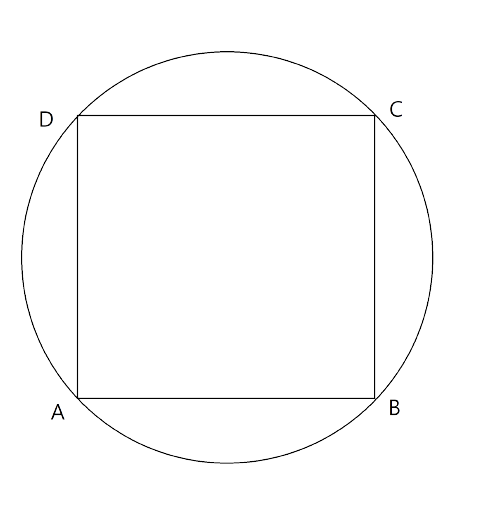
Ans: In a rhombus opposite angles are always equal.

Hence, $\angle BAD=\angle BCD$

Here ABCD is also a cyclic quadrilateral.

So, $\angle BAD+\angle BCD={{180}^{\circ }}$

$\Rightarrow 2\angle BAD={{180}^{\circ }}$ ($\because \angle BAD=\angle BCD$)

$\Rightarrow \angle BAD={{90}^{\circ }}$

∴$\angle BAD=\angle BCD={{90}^{\circ }}$

Similarly the other two angles are right angle and equal.

So, $\angle BAD=\angle BCD=\angle ADC=\angle ABC={{90}^{\circ }}$ and AB=BC=CD=AD.

Therefore the quadrilateral ABCD is a square.

21. In the given figure, AB=AC. Prove that DECB is an isosceles trapezium.

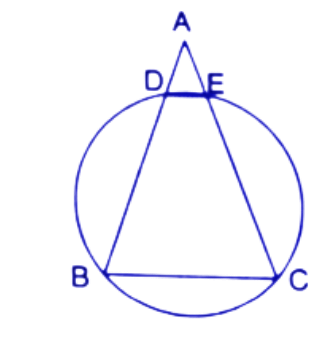
Ans: Given AB=AC------(1)

At first we join the points D and E.

∵ AB=AC

Therefore $\angle ABC=\angle ACB\Rightarrow \angle DBC=\angle ECB$

Here DBEC is a cyclic quadrilateral.

So, $\angle DEC+\angle DBC={{180}^{\circ }}$

$\Rightarrow \angle DEC+\angle ECB={{180}^{\circ }}$

So, DE||BC and given AB=AC

∴ $\angle AED=\angle ACB$ and $\angle ADE=\angle ABC$   (Corresponding angles)

Hence, $\angle AED=\angle ADE$

Therefore the sides AD=AE-----(2)

From eq.(1)-eq.(2)

$AB-AD=AC-AE$

$\Rightarrow BD=CE$

$\because ~DE||BC$ and $BD=CE$

Therefore DECB is an isosceles trapezium.

22. Two circles intersect at P and Q. Through P diameter PA and PB of the two circles are drawn. Show that the points A, Q and B are collinear.

Ans: 

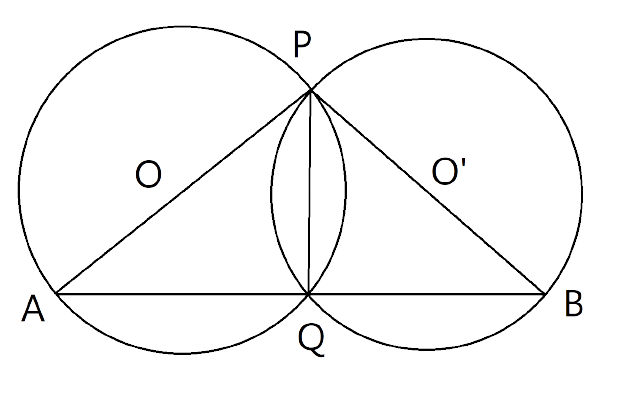
Let O and O’are the centres of the two intersecting circles and PA and PB are the diameters. Here Angles $\angle PQA$ and $\angle PQB$ are subtended by the diameters PA and PB respectively, which means these angles are made in semicircle and we know that if in a circle an angle is made in semicircle then that angle is right angle.

So, $PQA$and$PQB$are right angles.

$\angle PQA={{90}^{\circ }}$and $\angle PQB={{90}^{\circ }}$

Now on adding the above angles,

$\angle PQA+\angle PQB={{90}^{\circ }}+{{90}^{\circ }}={{180}^{\circ }}$

$\Rightarrow \angle PQA+\angle PQB={{180}^{\circ }}$

Thus AQB is a straight line. Hence point A,Q and b are collinear points.

23. The figure given below, shows a circle with centre O.

Given: $\angle AOC=a$ and $\angle ABC=b.$

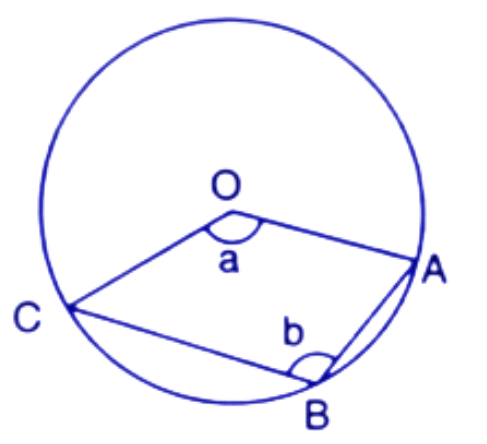
(i). Find the relationship between a and b.

Ans: We know that in a circle the angle at the centre is double the angle at any point on circumference subtended by the same chord.

So, $\angle ABC=\dfrac{1}{2}\times Reflex~\left( AOC \right)$

From the given figure, $\angle ABC=b$and $\angle AOC=a$

$\Rightarrow b=\dfrac{1}{2}\times ~\left( {{360}^{\circ }}-a \right)$

$\Rightarrow 2b={{360}^{\circ }}-a$

$\Rightarrow 2b+a={{360}^{\circ }}$-----(1)

Thus the relation b/w a and b is $2b+a={{360}^{\circ }}$

(ii). Find the measure of angle OAB, if OABC is a parallelogram.

Ans: Since OABC is a parallelogram, therefore opposite angles are equal i.e.

a=b

From eq.1

$\Rightarrow 2a+a={{360}^{\circ }}$

$\Rightarrow 3a={{360}^{\circ }}$

$\Rightarrow a={{120}^{\circ }}$

Since OABC is a parallelogram, Therefore opposite sides are parallel and the sum of corresponding angles is ${{180}^{\circ }}$.

So, OC||AB

$\angle COA+\angle OAB={{180}^{\circ }}$

$\Rightarrow a+\angle OAB={{180}^{\circ }}$ ($\angle COA=a$)

$\Rightarrow {{120}^{\circ }}+\angle OAB={{180}^{\circ }}$

$\Rightarrow \angle OAB={{180}^{\circ }}-{{120}^{\circ }}={{60}^{\circ }}$

Thus the value of angle $\angle OAB$ is ${{60}^{\circ }}$.

24. Two chords AB and CD intersect at point P inside the circle. Prove that the sum of the angles subtended by the arcs AC and BD at the centre O is equal to twice the angle APC.

Ans: 

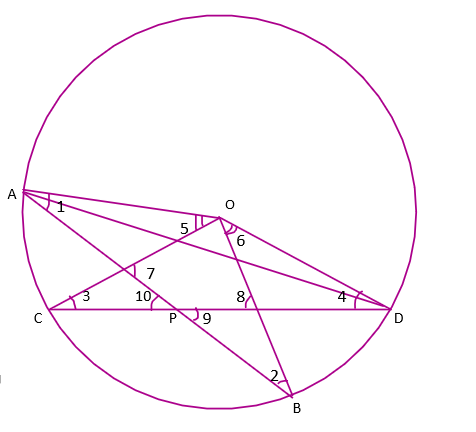
In a circle the angle at the centre is double the angle at any point on circumference  subtended by the same chord.

$\angle AOC=2\angle ADC$---------(1)

Similarly,

$\angle BOD=2\angle BAD$--------(2)

On adding eq. (1)&(2)

$\angle AOC~+~\angle BOD=2\left( \angle ADC+\angle BAD \right)$------------(3)

By the exterior angle property, In a triangle the exterior angle is equal to the sum of the opposite angles.

Now in $\Delta PAD$by using the exterior angle property

$\angle APC=\angle BAD+\angle ADC$-------------(4)

By eq. (3) & (4)

$\angle AOC~+~\angle BOD=2\angle APC$

Thus the sum of the angles subtended by the arcs AC and BD at the centre O is equal to twice the angle APC.

25. In the given figure, RS is the diameter of the circle. NM is parallel to RS and $\angle MRS={{29}^{\circ }}$. Calculate:

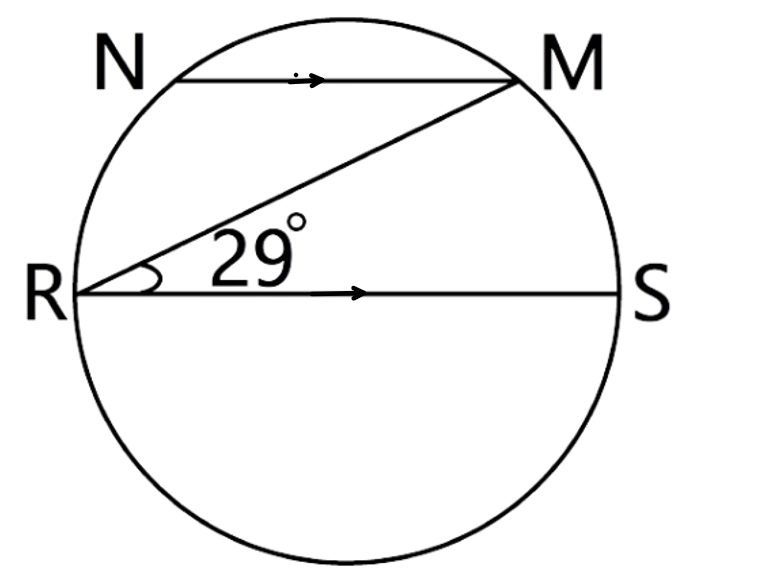
(i).$\angle RNM$

Ans: First we join the point N to R and M to S as 

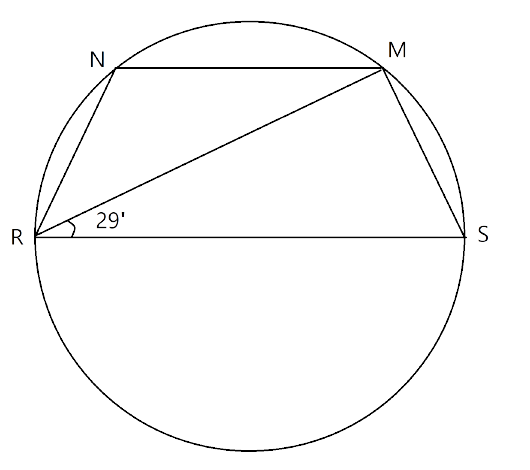
Here RS is the diameter and angle $\angle RMS$ is the centre made in a circle and we know that the angle made in the semicircle is the right angle.

So, $\angle RMS={{90}^{\circ }}$

By the angle sum property, the sum of the interior angles in a triangle is ${{180}^{\circ }}$

In $\Delta RMS$,

$\angle RMS+\angle RSM+\angle MRS={{180}^{\circ }}$

$\Rightarrow {{90}^{\circ }}+\angle RSM+{{29}^{\circ }}={{180}^{\circ }}$

$\Rightarrow \angle RSM+{{119}^{\circ }}={{180}^{\circ }}$

$\Rightarrow \angle RSM={{180}^{\circ }}-{{119}^{\circ }}={{61}^{\circ }}$

Since, NMRS is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$.

$\angle RNM+\angle RSM={{180}^{\circ }}$

$\Rightarrow \angle RNM+{{61}^{\circ }}={{180}^{\circ }}$  (∵$\angle RSM={{61}^{\circ }}$)

$\Rightarrow \angle RNM={{180}^{\circ }}-{{61}^{\circ }}={{119}^{\circ }}$

Thus the value of $\angle RNM$ is ${{119}^{\circ }}$.

(ii). $\angle NRM$

Ans: Since, NM||RS (Given)

$\angle NMR=\angle MRS={{29}^{\circ }}$(Alternate angles)

Thus, $\angle NMS=\angle NMR+\angle RMS={{29}^{\circ }}+{{90}^{\circ }}={{119}^{\circ }}$

In a cyclic quadrilateral the opposite angles are supplementary.

$\angle NRS+\angle NMS={{180}^{\circ }}$

$\Rightarrow \angle NRM+\angle MRS+{{119}^{\circ }}={{180}^{\circ }}$

$\Rightarrow \angle NRM+{{29}^{\circ }}+{{119}^{\circ }}={{180}^{\circ }}$

$\Rightarrow \angle NRM={{180}^{\circ }}-{{148}^{\circ }}={{32}^{\circ }}$

Thus the value of angle $\angle NRM$ is ${{32}^{\circ }}$

26. In the figure, given alongside, AB//CD and O is the centre of the circle. If $\angle ADC={{25}^{\circ }}$ find the angle AEB. Give reasons in support of your answer.

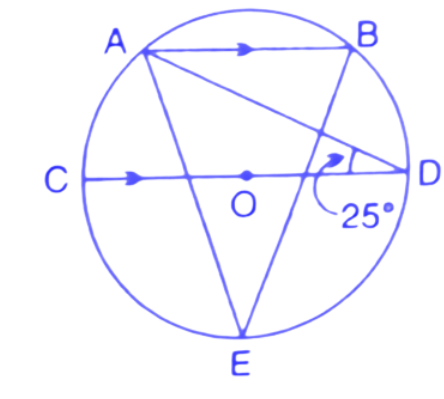
Ans: First we join the points A to C, B to D and B to C.

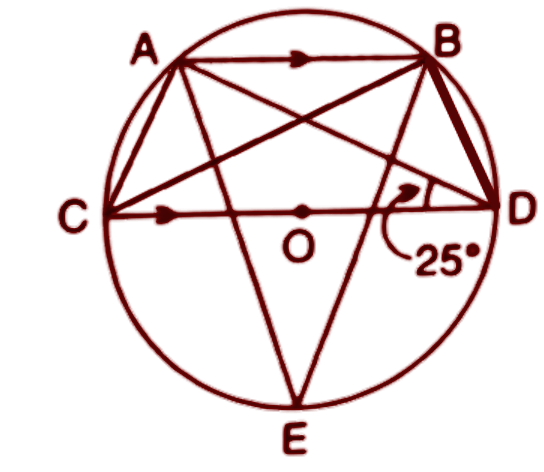
We know that the angle made in a semicircle is the right angle. Here CD is the diameter and $\angle CAD$ & $\angle CBD$ are subtended by the diameter CD so these angles are made in semicircle. Hence 

$\angle CAD=\angle CBD={{90}^{\circ }}$ 

From the figure, AB||CD and AD is a transversal line.

So,  $\angle ADC=\angle BAD={{25}^{\circ }}$ (Alternate angle)

$\angle BAC=\angle BAD+\angle CAD$

$\Rightarrow \angle BAC={{25}^{\circ }}+{{90}^{\circ }}={{115}^{\circ }}$

ABDC is a cyclic quadrilateral and we know that in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$.

$\angle BAC+\angle BDC={{180}^{\circ }}$

$\Rightarrow {{115}^{\circ }}+\angle BDC={{180}^{\circ }}$  (∵$\angle BAC={{115}^{\circ }}$)

$\Rightarrow \angle BDC={{65}^{\circ }}$

$\Rightarrow \angle ADC+\angle ADB={{65}^{\circ }}$

$\Rightarrow \angle ADB={{65}^{\circ }}-{{25}^{\circ }}={{40}^{\circ }}$

In a circle, the angle subtended by the same chord on the circumference is always equal. Here $\angle ADB$ and $\angle AEB$ are subtended by the chord AB.

Hence, $\angle AEB=\angle ADB={{40}^{\circ }}$

Thus the value of angle $\angle AEB$is$~{{40}^{\circ }}$.

27. Two circles intersect at P and Q. Through P, a straight line APB is drawn to meet the circles in A and B. Through Q, a straight line is drawn to meet the circles at C and D. Prove that AC is parallel to BD.

Ans: At first we join the points AC , PQ and BD.

Since, APQC is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$.

So, $\angle CAP+\angle PQC={{180}^{\circ }}$------(1)

Similarly,  PBDQ is a cyclic quadrilateral.

$\angle DBP+\angle PQD={{180}^{\circ }}_{{}}$----------(2)

Since, CQD is a straight line. Hence,

$\angle PQD+\angle PQC={{180}^{\circ }}$----------(3)

From eq.(1),(2)&(3)

$\angle CAP+\angle PQC+\angle DBP+\angle PQD={{180}^{\circ }}+\angle PQD+\angle PQC$

$\Rightarrow \angle CAP+\angle DBP={{180}^{\circ }}$

$\because ~\angle CAP=\angle CAB$ & $\angle DBP=\angle DBA$

$\Rightarrow \angle CAB+\angle DBA={{180}^{\circ }}$

Here AB is the transversal line and angles $\angle CAB$ and $\angle DBA$ are the interior angles on the same side of the transversal. We know that if a transversal line intersects a pair of straight lines such that the sum of interior angles on the same side of the transversal is ${{180}^{\circ }}$ then the lines are parallel.

Hence, AC||BD.

28. ABCD is a cyclic quadrilateral in which AB and DC on being produced, meet at P such that PA=PD. Prove that AD is parallel to BC.

Ans: 

Given, PA=PD

Hence, $\angle PAD=\angle PDA$---------(1)

Here PAB and PDC are straight lines.

Therefore, $\angle PAD+\angle BAD={{180}^{\circ }}$

$\Rightarrow \angle BAD={{180}^{\circ }}-\angle PAD$--------(1)

and, for straight line PDC

$\angle PDA+\angle CDA={{180}^{\circ }}$

$\Rightarrow \angle CDA={{180}^{\circ }}-\angle PDA={{180}^{\circ }}-\angle PAD$   (∵$\angle PAD=\angle PDA$)----(3)

ABCD is a cyclic quadrilateral and we know that in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$.

$\angle ABC+\angle CDA={{180}^{\circ }}$

$\Rightarrow \angle ABC={{180}^{\circ }}-\angle CDA$

$\Rightarrow \angle ABC={{180}^{\circ }}-\left( {{180}^{\circ }}-\angle PAD \right)$ (From eq. 3)

$\Rightarrow \angle ABC=\angle PAD$----(3)

And, 

$\angle DCB+\angle BAD={{180}^{\circ }}$

$\Rightarrow \angle DCB={{180}^{\circ }}-\angle BAD$

$\Rightarrow \angle DCB={{180}^{\circ }}-\left( {{180}^{\circ }}-\angle PAD \right)$   (From eq. 2)

$\Rightarrow \angle DCB=\angle PAD$----(4)

By eq. (1),(2),(3) and (4), we get

$\angle ABC=\angle DCB=\angle PAD=\angle PDA$

We know that if corresponding angles are equal then the lines are parallel.

Hence, AD||BC.

29. AB is a diameter of the circle APBR as shown in a figure. APQ and RBQ are straight lines, Find: 

(i).$\angle PRB$

Ans: In a circle, Angles subtended by the same chord on the circumference are always the same.

Here Angles $\angle PAB$and $\angle PRB$ are subtended by the chord PB.

So, $\angle PRB=\angle PAB={{35}^{\circ }}$

Thus the value of $\angle PRB$ is ${{35}^{\circ }}$.

(ii). $\angle PBR$

Ans: In a circle angle made by the diameter is a right angle. Here $\angle APB$

Is made by the diameter AB. Hence $\angle APB={{90}^{\circ }}$.

Given that APQ is a straight line , So $\angle APB+\angle BPQ={{180}^{\circ }}$ (supplementary angles)

$\angle BPQ={{180}^{\circ }}-\angle APB={{180}^{\circ }}-{{90}^{\circ }}={{90}^{\circ }}$

Now, In a triangle the exterior angle is equal to the sum of opposite interior angles of the triangle.

$\angle PBR=\angle BPQ+\angle PQB={{90}^{\circ }}+{{25}^{\circ }}={{115}^{\circ }}_{{}}$

Thus the value of angle $\angle PBR$ is ${{115}^{\circ }}_{{}}$

(iii). $\angle BPR$

Ans: By the angle sum property, the sum of all interior angles is a triangle is always ${{180}^{\circ }}$.

By using angle sum property in $\Delta PBR$

$\angle BPR+\angle PRB+\angle PBR={{180}^{\circ }}$

$\Rightarrow \angle BPR+{{35}^{\circ }}+{{115}^{\circ }}={{180}^{\circ }}$

$\Rightarrow \angle BPR={{180}^{\circ }}-{{150}^{\circ }}={{30}^{\circ }}$

Thus the value of angle $\angle BPR$ is ${{30}^{\circ }}$

30. In the given figure, SP is a bisector of $\angle RPT$ and PQRS is a cyclic quadrilateral, Prove that: SQ=SR.

Ans: Given that PQRS is a cyclic quadrilateral.

In a cyclic quadrilateral, the sum of opposite angles is always ${{180}^{\circ }}$

So, 

$\angle QPS+\angle QRS={{180}^{\circ }}$-----(1)

Since QPT is a straight line. So,

$\angle QPS+\angle SPT={{180}^{\circ }}$------(2)

From eq.(1) and (2)

$\angle QRS=\angle SPT$---------(3)

PS is the bisector of $\angle RPT$.

Therefore, $\angle RPS=\angle SPT$---------(4)

In a circle the angles subtended by the same chord are always equal.

Here angles $\angle SQR$ and $\angle RPS$ are subtended by the chord RS.

Hence $\angle RQS=\angle RPS$--------(5)

From eq.(3),(4) and (5)

$\angle RQS=\angle QRS$

We know that in a triangle if two angles are equal then their opposite sides are also equal.

Therefore, QS=SR   (∵$\angle RQS=\angle QRS$)

31. In the figure, O is the centre of the circle, $\angle AOE={{150}^{\circ }}$, $\angle DAO={{51}^{\circ }}$. Calculate the sizes of the angles CEB and OCE.

Ans: In a circle the angle at the centre is doubled the angle at the circumference by the same chord.

$\angle ADE=\dfrac{1}{2}\times \left( \operatorname{Re}flex~angle~of~AOE \right)$

$\Rightarrow \angle ADE=\dfrac{1}{2}\times \left( {{360}^{\circ }}-{{150}^{\circ }} \right)$

$\Rightarrow \angle ADE=\dfrac{1}{2}\times \left( {{210}^{\circ }} \right)={{105}^{\circ }}$

In a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$

$\angle DAB+\angle BED={{180}^{\circ }}$

$\Rightarrow \angle BED={{180}^{\circ }}-\angle DAB$

$\Rightarrow \angle BED={{180}^{\circ }}-{{51}^{\circ }}={{129}^{\circ }}$  ($\angle DAB$=$\angle DAO$=${{51}^{\circ }}$)

DEC is a straight line and the sum of angle on a straight line is ${{180}^{\circ }}.$

$\angle BED+\angle CEB={{180}^{\circ }}$

$\Rightarrow \angle CEB={{180}^{\circ }}-\angle BED={{180}^{\circ }}-{{129}^{\circ }}={{51}^{\circ }}$

Thus the value of $\angle CEB$ is ${{51}^{\circ }}$.

By using the angle sum property in $\Delta ADC$

$\angle ADC+\angle OCE+\angle DAC={{180}^{\circ }}$

$\Rightarrow \angle OCE={{180}^{\circ }}-\angle ADC-\angle DAC$

$\Rightarrow \angle OCE={{180}^{\circ }}-{{105}^{\circ }}-{{51}^{\circ }}={{180}^{\circ }}-{{156}^{\circ }}$ ($\because \angle ADC=\angle ADE={{105}^{\circ }}$)

$\Rightarrow \angle OCE={{24}^{\circ }}$

Thus the value of angle $\angle OCE$ is ${{24}^{\circ }}$.

32. In the figure, given below, P and Q are the centres of two circles intersecting at B and C. ACD is a straight line. Calculate the numerical value of x.

Ans: We know that the angle at the centre is doubled the angle at any point of circumference subtended by the same chord.

$\angle APB=2\times \angle ACB$

 $\angle ACB=\dfrac{1}{2}\times \angle APB=\dfrac{1}{2}\times {{150}^{\circ }}={{75}^{\circ }}$

Sum of the angles in a straight line is ${{180}^{\circ }}$

For straight line ACD,

$\angle ACB+\angle BCD={{180}^{\circ }}$

$\Rightarrow \angle BCD={{180}^{\circ }}-\angle ACB={{180}^{\circ }}-{{75}^{\circ }}={{105}^{\circ }}$

In a circle, The angle at the centre is doubled the angle at the circumference subtended by the same chord.

$\angle BQD=2\times \angle BCD$

$\Rightarrow \angle BQD=2\times {{105}^{\circ }}={{210}^{\circ }}$

Now, $\angle BQD+x={{360}^{\circ }}$

$x={{360}^{\circ }}-\angle BQD$

$\Rightarrow x={{360}^{\circ }}-{{210}^{\circ }}={{150}^{\circ }}$

Thus the value of x is ${{150}^{\circ }}$

33. The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given $\angle APB={{a}^{\circ }}$. Calculate in terms of ${{a}^{\circ }}$, the value of:

(i). Obtuse $\angle AOB$

(ii). $\angle ACB$

(iii). $\angle ADB$

Give reasons for your answer clearly.

(i). obtuse $\angle AOB$

Ans: In a circle the angle at the centre is doubled the angle at the circumference subtended by the same arc.

Here in smaller circles angle $\angle APB$ and angle at centre $\angle AOB$ are subtended by the same arc.

Therefore, $\angle AOB=2.\angle APB$

$\angle AOB=2{{a}^{\circ }}$  (∵$\angle APB={{a}^{\circ }}$)

Thus the value of $\angle AOB$ is $2{{a}^{\circ }}$

(ii). $\angle ACB$

Ans: We know that in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}.$Since OACB is a cyclic quadrilateral.

So, $\angle AOB+\angle ACB={{180}^{\circ }}$

$\Rightarrow \angle ACB={{180}^{\circ }}-\angle AOB$

$\Rightarrow \angle ACB={{180}^{\circ }}-2{{a}^{\circ }}$

Thus the value of $\angle ACB$ is ${{180}^{\circ }}-2{{a}^{\circ }}$.

(iii). $\angle ADB$

Ans: Here join AB, AD and BD.

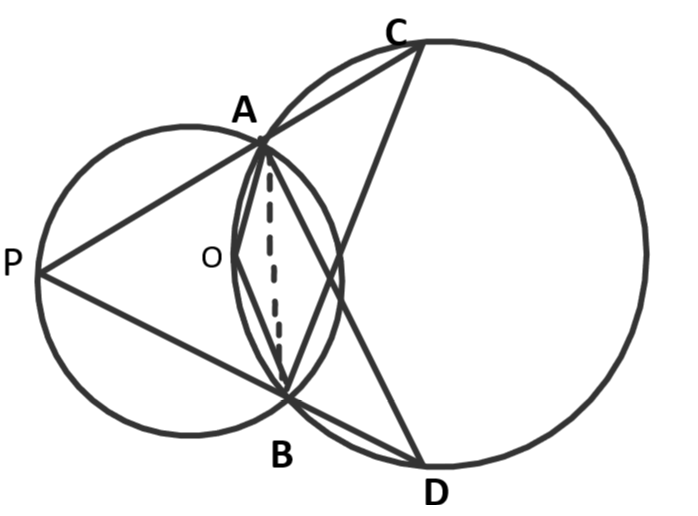
In a circle angles subtended by the same chord are always equal. Here angles 

$\angle ADB$and $\angle ACB$ are subtended by the same chord AB. 

Therefore, $\angle ADB=\angle ACB$

$\Rightarrow \angle ADB={{180}^{\circ }}-2{{a}^{\circ }}$  (∵$\angle ACB={{180}^{\circ }}-2{{a}^{\circ }}$)

Thus the value of $\angle ADB$ is ${{180}^{\circ }}-2{{a}^{\circ }}$.

34. In the given figure, O is the centre of the circle and $\angle ABC={{55}^{\circ }}$. Calculate the values of x and y. 

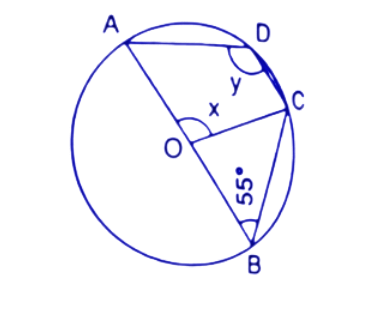
Ans: In a circle angle at the centre is doubled the angle at the circumference subtended by the same chord.

So,  $\angle AOC=2\times \angle ABC$

$\Rightarrow \angle AOC=2\times {{55}^{\circ }}={{110}^{\circ }}$

From the figure, $x=\angle AOC$

$\Rightarrow x={{110}^{\circ }}$

ABCD is a cyclic quadrilateral and we know that in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$.

$\angle ADC+\angle ABC={{180}^{\circ }}$

$\Rightarrow \angle ADC={{180}^{\circ }}-{{55}^{\circ }}={{125}^{\circ }}$

Since , $y=\angle ADC$

So, $y={{125}^{\circ }}$

Thus the values of x, y are ${{110}^{\circ }}$ & ${{125}^{\circ }}$ respectively.

35. In the given figure, A is the centre of the circle, ABCD is a parallelogram and CDE is a straight line. Prove that: $\angle BCD=2\angle ABE$

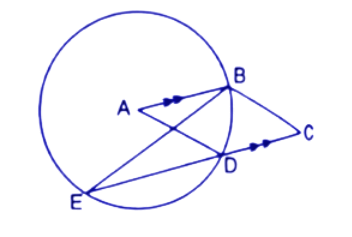
Ans: In a circle the angle at the centre is double the angle at the circumference subtended by the same chord.

$\angle BAD=2\angle BED$------(1)

Since $AB||EC$

$\angle BED=\angle ABE$  (Alternate angle)---------(2)

From eq.(1) and (2).

$\angle BAD=2\angle ABE$-----(3)

ABCD is a parallelogram hence the opposite angles in a parallelogram are equal.

So, $\angle BAD=\angle BCD$------(4)

From eq.(3) and (4)

$\angle BCD=2\angle ABE$

Hence proved.

36. ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given $\angle BED={{65}^{\circ }}$; calculate:

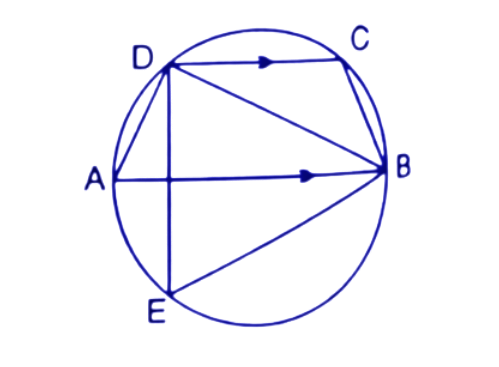
(i). $\angle DAB$

Ans: The angle subtended by the same chord 

Are always equal. Here angles $\angle DAB$ and $\angle BED$ are subtended by the same chord BD. 

Hence, $\angle DAB=\angle BED={{65}^{\circ }}$

Thus the value of $\angle DAB$ is ${{65}^{\circ }}$.

(ii). $\angle BDC$

Ans: In a triangle by the angle sum property the sum of all the interior angles is ${{180}^{\circ }}$.

In$\Delta ABD$ By using angle sum property,

$\angle ADB+\angle ABD+\angle DAB={{180}^{\circ }}$

$\Rightarrow {{90}^{\circ }}+\angle ABD+{{65}^{\circ }}={{180}^{\circ }}$

$\Rightarrow \angle ABD={{180}^{\circ }}-{{155}^{\circ }}={{25}^{\circ }}$

Since, Lines AB and CD are parallel. 

$\angle BDC=\angle ABD$ (Alternate angles)

$\Rightarrow \angle BDC={{25}^{\circ }}$

Thus the value of $\angle BDC$ is  ${{25}^{\circ }}$.

37. In the given figure, AB is the diameter of the circle. Chord ED is parallel to AB and $\angle EAB={{63}^{\circ }}.$ Calculate:

(i). $\angle EBA$

Ans:  The angle made in the semicircle is always ${{90}^{\circ }}.$

Here $\angle AEB$ is subtended by the diameter AB. so the

$\angle AEB$ is made in semicircle. 

Hence, $\angle AEB={{90}^{\circ }}$

By the angle sum property in a triangle the sum of all interior angles is  ${{180}^{\circ }}.$

In $\Delta AEB$ by using the angle sum property, 

$\angle AEB+\angle EBA+\angle BAE={{180}^{\circ }}$

$\angle EBA={{180}^{\circ }}-{{90}^{\circ }}-{{63}^{\circ }}={{180}^{\circ }}-{{153}^{\circ }}={{27}^{\circ }}$

Thus the value of $\angle EBA$ is ${{27}^{\circ }}$.

(ii). $\angle BCD$

Ans: Given that ED||AB

Hence $\angle EBA=\angle DEB$ (Alternate angle) 

$\Rightarrow \angle DEB=\angle EBA={{27}^{\circ }}$ 

Since BCDE is a cyclic quadrilateral and we know that in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$.

Hence $\angle BCD+\angle DEB={{180}^{\circ }}$

$\Rightarrow \angle BCD={{180}^{\circ }}-{{27}^{\circ }}={{153}^{\circ }}$

Thus the value of $\angle BCD$ is ${{153}^{\circ }}$.

38. In the given figure, AB is the diameter of the circle with centre o. DO is parallel to CB and $\angle DCB={{120}^{\circ }}$, Calculate:

(i).$\angle DAB,$

Ans: Since ABCD is a cyclic quadrilateral. The sum of opposite angles in a cyclic quadrilateral is ${{120}^{\circ }}$

$\angle DAB+\angle DCB={{180}^{\circ }}$

$\Rightarrow \angle DAB={{180}^{\circ }}-\angle DCB={{180}^{\circ }}-{{120}^{\circ }}={{60}^{\circ }}$

Thus the value of $\angle DAB$ is ${{60}^{\circ }}$.

(ii).$\angle DBA$

Ans: Angle subtended by the diameter at any point on circumference is ${{90}^{\circ }}$

So, $\angle ADB={{90}^{\circ }}$ (Subtended  by the diameter AB)

By the angle sum property in $\Delta ADB$,

$\angle ADB+\angle DAB+\angle DBA={{180}^{\circ }}$

$\Rightarrow \angle DBA={{180}^{\circ }}-{{90}^{\circ }}-{{60}^{\circ }}={{30}^{\circ }}$

Thus the value of $\angle DBA$ is ${{30}^{\circ }}$.

(iii).$\angle DBC$

Ans: Since OD=OB (Radii of circle)

∴ $\angle OBD=\angle ODB$ (opposite angles of equal sides are equal)

$\angle OBD=\angle ABD={{30}^{\circ }}$(Same angle)

$\therefore \angle ODB={{30}^{\circ }}$

Given, OD||BC

$\angle DBC=\angle ODB={{30}^{\circ }}$(Alternate angles)

Thus the value of $\angle DBC$ is ${{30}^{\circ }}$.

(iv).$\angle ADC$. Also show that the $\Delta AOD$ is an equilateral triangle 

Ans: Since ABCD is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$

So, $\angle DAB+\angle BCD={{180}^{\circ }}$

$\Rightarrow \angle BCD={{180}^{\circ }}-{{60}^{\circ }}={{120}^{\circ }}$ (∵$\angle DAB={{60}^{\circ }}$)

By using angle sum property in $\Delta BCD$,

$\angle BCD+\angle DBC+\angle BDC={{180}^{\circ }}$

$\Rightarrow \angle BDC={{180}^{\circ }}-{{120}^{\circ }}-{{30}^{\circ }}={{30}^{\circ }}$

Now, $\angle ADC=\angle BDC+\angle ADB$

$\Rightarrow \angle ADC={{30}^{\circ }}+{{90}^{\circ }}={{120}^{\circ }}$

Thus the value of $\angle ADC$is ${{120}^{\circ }}$.

In $\Delta AOD,$

OA=OD (Radii of circle)

∴$\angle ODA=\angle DAO$

From Part (i) $\angle DAB={{60}^{\circ }}$

$\angle DAO=\angle DAB={{60}^{\circ }}$

$\angle ODA=\angle DAO={{60}^{\circ }}$

$\Rightarrow \angle ODA=\angle DAO=\angle AOD={{60}^{\circ }}$

Therefore the triangle AOD is an equilateral triangle.

39. In the given figure, I is the incentre of $\Delta ABC$, BI when produced meets the circumcircle of  $\Delta ABC$ at D. Given $\angle BAC={{55}^{\circ }}$ and $\angle ACB={{65}^{\circ }};$ Calculate:

(i). $\angle DCA$

Ans: Join the Points IA, IC , AD and CD.

IB  is angle bisector of angle $\angle ABC$.

$\angle ABD=\dfrac{1}{2}\times \angle ABC$----(1)

By using the angle sum property in $\Delta ABC$,

$\angle ABC+\angle ACB+\angle BAC={{180}^{\circ }}$

$\Rightarrow \angle ABC={{180}^{\circ }}-{{55}^{\circ }}-{{65}^{\circ }}={{60}^{\circ }}$

By putting above value in eq. (i)

$\angle ABD=\dfrac{1}{2}\times {{60}^{\circ }}={{30}^{\circ }}$

The angles subtended by the same chord are equal. Angles $\angle ABD$ and $\angle DCA$ subtended by the chord AD.

So, $\angle DCA=\angle ABD={{30}^{\circ }}$

Thus the value of $\angle DCA$ is ${{30}^{\circ }}$.

(ii). $\angle DAC$

Ans: IB is the angle bisector of $\angle ABC$. 

$\Rightarrow \angle ABD=\angle DBC={{30}^{\circ }}$ (From (i) part)

Angles subtended by the same chord at any point on circumference are equal. 

Angles $\angle DAC$ and $\angle DBC$ subtended by the same chord DC.

So, $~\angle DAC=\angle DBC={{30}^{\circ }}$  (∵$\angle DBC={{30}^{\circ }}$)

Thus the value of $\angle DAC$ is ${{30}^{\circ }}$.

(iii). $\angle DCI$

Ans: CI is the angle bisector of $\angle ACB$.

$\angle ACI=\dfrac{1}{2}\times \angle ACB=\dfrac{1}{2}\times {{65}^{\circ }}={{32.5}^{\circ }}$

$\angle DCI=\angle ACI+\angle DCA$

$\Rightarrow \angle DCI={{32.5}^{\circ }}+{{30}^{\circ }}$

$\Rightarrow \angle DCI={{62.5}^{\circ }}$

Thus the value of $\angle DCI$ is ${{62.5}^{\circ }}$.

(iv). $\angle AIC$

Ans: AI is the angle bisector of $\angle BAC$.

Therefore, $\angle IAC=\dfrac{1}{2}\times \angle BAC=\dfrac{1}{2}\times {{55}^{\circ }}={{27.5}^{\circ }}$

Now, by using the angle sum property in $\Delta IAC$

$\angle IAC+\angle AIC+\angle ACI={{180}^{\circ }}$

$\Rightarrow \angle AIC={{180}^{\circ }}-\angle IAC-\angle ACI$

$\Rightarrow \angle AIC={{180}^{\circ }}-{{27.5}^{\circ }}-{{32.5}^{\circ }}={{120}^{\circ }}$

Thus the value of $\angle AIC$ is ${{120}^{\circ }}$

40. In the triangle ABC is inscribed in a circle. The bisectors of angles BAC, ABC and ACB meet the circumcircle of the triangle at points P,Q and R respectively. Prove that:

Ans: Join Points PR and PQ.

(i). $\angle ABC=2\angle APQ$

Ans: BQ is the angle bisector of $\angle ABC$.

So, $\angle ABQ=\dfrac{1}{2}\times \angle ABC$

$\Rightarrow \angle ABC=2\angle ABQ$-------(1)

Angles subtended by the same arc on circumference are always equal. Angles 

$\angle ABQ$ and $\angle APQ$ are subtended by the same arc AQ.

$\angle ABQ=\angle APQ$--------(2)

From eq.(1) and (2).

$\angle ABC=2\angle APQ$

Hence proved.

(ii). $\angle ACB=2\angle APR$

Ans: CR is an angle bisector of $\angle ACB$.

$\angle ACR=\dfrac{1}{2}\times \angle ACB$

$\Rightarrow \angle ACB=2\angle ACR$------(3)

In a circle angles subtended by the same arc on circumference are equal. Angles $\angle APR$ and $\angle ACR$ are subtended by the same arc AR.

So, $\angle APR=\angle ACR$------(4)

From eq.(3) and (4)

$\angle ACB=2\angle APR$

Hence Proved.

(iii). $\angle QPR={{90}^{\circ }}-\dfrac{1}{2}\angle BAC$

Ans: Since From the (i) and (ii) parts

$\angle APQ=\dfrac{1}{2}\times \angle ABC$ and $\angle APR=\dfrac{1}{2}\times \angle ACB$

Now, On additing

 $\angle APQ+\angle APR=\dfrac{1}{2}\times \angle ABC+\dfrac{1}{2}\times \angle ACB$

$\angle APQ+\angle APR=\dfrac{1}{2}\times \left( \angle ABC+\angle ACB \right)$

$\Rightarrow \angle APQ+\angle APR=\dfrac{1}{2}\times \left( {{180}^{\circ }}-\angle BAC \right)$   (∵ $\angle ABC+\angle ACB+\angle BAC={{180}^{\circ }}$)

$\Rightarrow \angle QPR={{90}^{\circ }}-\dfrac{1}{2}\times \angle BAC$  (∵ From figure $\angle APQ+\angle APR=\angle QPR$)

Hence proved.

41. Calculate the angles x,y and z if :

$\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}$

Ans:

Let $\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=k$

$\Rightarrow x=3k,y=4k,~z=5k$

$\angle BCP=x$ (Vertically opposite)

Now by using exterior angle property, the exterior angle is equal to the sum of opposite angles.

$\angle ABC=\angle BPC+\angle BCP$

$\Rightarrow \angle ABC=x+y$

$\Rightarrow \angle ABC=3k+4k=7k$    (∵$x=3k,y=4k$)

Also, $\angle ADC=x+z$

$\angle ADC=3k+5k=8k$  (∵$x=3k,y=5k$)

ABCD is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$

$\angle ABC+\angle ADC={{180}^{\circ }}$

$\Rightarrow 7k+8k={{180}^{\circ }}$

$\Rightarrow 15k={{180}^{\circ }}$

$\Rightarrow k={{12}^{\circ }}$

Therefore the values of x,y andz.

$x=3k=3\times {{12}^{\circ }}={{36}^{\circ }}$

$y=4k=4\times {{12}^{\circ }}={{48}^{\circ }}$

$z=5k=5\times {{12}^{\circ }}={{60}^{\circ }}$

42. In the given figure, AB=AC=CD and $\angle ADC={{38}^{\circ }}$. Calculate :

(i). $\angle ABC$

Ans: Given AC=CD

$\therefore \angle CAD=\angle ADC={{38}^{\circ }}$ (Given $\angle ADC={{38}^{\circ }}$)

By using angle sum property in $\Delta ADC$

$\angle CAD+\angle ADC+\angle ACD={{180}^{\circ }}$

$\Rightarrow \angle ACD={{180}^{\circ }}-{{38}^{\circ }}-{{38}^{\circ }}={{104}^{\circ }}$

From the figure, BCD is a straight line.

$\angle ACB+\angle ACD={{180}^{\circ }}$

$\Rightarrow \angle ACB={{180}^{\circ }}-{{104}^{\circ }}={{76}^{\circ }}$

Given, AB=AC

$\angle ABC=\angle ACB$  (Opposite angles of equal sides are equal)

$\Rightarrow \angle ABC={{76}^{\circ }}$

Thus the value of $\angle ABC$ is ${{76}^{\circ }}$.

(ii). Angle BEC

By using the angle sum property in $\Delta ABC$

$\angle ABC+\angle BAC+\angle ACB={{180}^{\circ }}$

$\Rightarrow \angle BAC={{180}^{\circ }}-{{76}^{\circ }}-{{76}^{\circ }}={{38}^{\circ }}$ (∵$\angle ABC=\angle ACB={{76}^{\circ }}$)

Angles subtended by the same chord on the circumference are equal.

Angles $\angle BAC~\And \angle BEC$ are subtended by the same chord BC.

Therefore, $\angle BEC=\angle BAC={{38}^{\circ }}$

43. In the given figure, AC is the diameter of the circle, centre O. Chord BD is perpendicular to AC. Write down the angles p,q and r in terms of x.

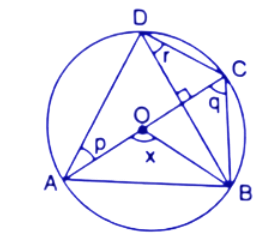
Ans: In a circle the angle at the centre is double the angle at any point on circumference subtended by the same chord.

$\angle AOB=2\angle ADB$----(1)

Angles subtended by the same chord on the circumference are equal.

$\angle ADB=\angle ACB$----(2)

From eq.(1) and (2)

$\angle AOB=2\angle ACB$

$\Rightarrow x=2q$

$\Rightarrow q=\dfrac{x}{2}$

The angles subtended by the same chord on the circumference are equal. Here angles $\angle DAC~\And ~\angle DBC$ are subtended by the same chord DC.

$\angle DAC=\angle DBC$

By exterior angle property, ${{90}^{\circ }}=q+\angle DBC$

$\Rightarrow p={{90}^{\circ }}-q$ 

$\Rightarrow p={{90}^{\circ }}-\dfrac{x}{2}$  (∵ $q=\dfrac{x}{2}$)

In a circle, the angle made by the diameter is the right angle. 

$\angle ADC={{90}^{\circ }}$

$\Rightarrow \angle ADB+r={{90}^{\circ }}$

$\Rightarrow q+r={{90}^{\circ }}$

$\Rightarrow r={{90}^{\circ }}-q$

$\Rightarrow r={{90}^{\circ }}-\dfrac{x}{2}$ 

Thus the values of p,q and r are ${{90}^{\circ }}-\dfrac{x}{2}$,$\dfrac{x}{2}$ and ${{90}^{\circ }}-\dfrac{x}{2}$ respectively.

44. In the given figure, AC is the diameter of the circle with centre O. CD and BE are parallel. Angle $\angle ADB={{80}^{\circ }}$ and $\angle ACE={{10}^{\circ }}$. Calculate :

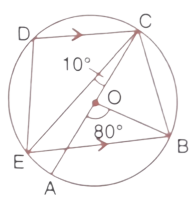
(i). Angle BEC,

Ans: AOC is a straight line. 

Hence, $\angle AOB+\angle BOC={{180}^{\circ }}$

$\angle BOC={{180}^{\circ }}-{{80}^{\circ }}={{100}^{\circ }}$

Angle at the centre is doubled the angle at the circumference subtended by the same chord. 

So, $\angle BOC=2\angle BEC$

$\Rightarrow \angle BEC=\dfrac{1}{2}\times \angle BOC=\dfrac{{{100}^{\circ }}}{2}={{50}^{\circ }}$

Thus the value of $\angle BEC$ is ${{50}^{\circ }}$

(ii)Angle BCD,

Ans: DC||EB

$\angle DCE=\angle BEC$ (Alternate angles)

$\Rightarrow \angle DCE={{50}^{\circ }}$

The angle at the centre is doubled the angle at the circumference subtended by the same chord.

$\angle AOB=2\angle ACB$

$\angle ACB=\dfrac{1}{2}\times \angle AOB=\dfrac{{{80}^{\circ }}}{2}={{40}^{\circ }}$

$\angle BCD=\angle ACB+\angle DCE+\angle ACE$

$\Rightarrow \angle BCD=\angle ACB+\angle DCE+\angle ACE$

$\Rightarrow \angle BCD={{40}^{\circ }}+{{50}^{\circ }}+{{10}^{\circ }}={{100}^{\circ }}$

(iii). Angle CED

Ans: BCDE is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$

$\angle BCD+\angle DEB={{180}^{\circ }}$

$\Rightarrow \angle DEB={{180}^{\circ }}-{{100}^{\circ }}={{80}^{\circ }}_{{}}$

$\Rightarrow \angle BEC+\angle CED={{80}^{\circ }}$   (∵$\angle DEB=\angle BEC+\angle CED$)

$\Rightarrow \angle CED={{80}^{\circ }}-\angle BEC={{80}^{\circ }}-{{50}^{\circ }}={{30}^{\circ }}$

Thus the value of $\angle CED$ is ${{30}^{\circ }}$.

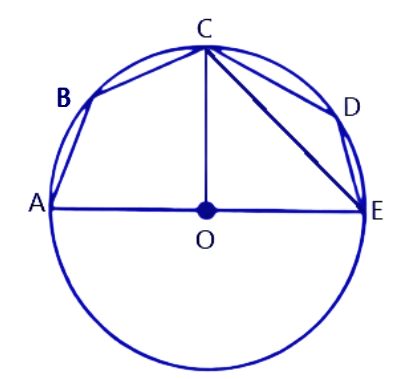
45. In the given figure, AE is the diameter of the circle. Write down the numerical value of $\angle ABC+\angle CED$. Give reasons for your answer.

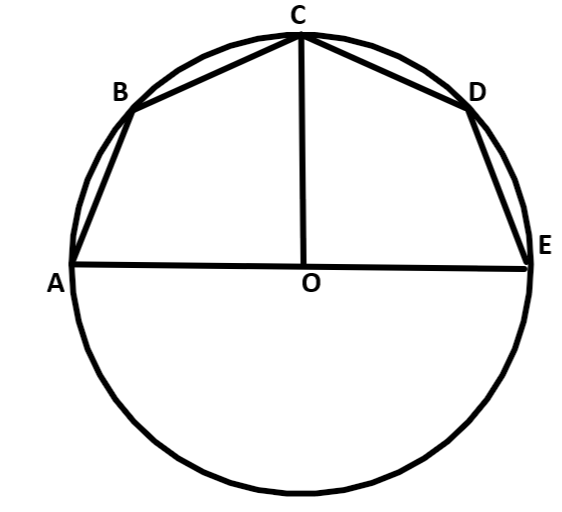
Ans:

Join the points CE and OC.

AOE is a straight line.

Hence, $\angle AOC=\angle COE=\dfrac{{{180}^{\circ }}}{2}={{90}^{\circ }}$ ($CO\bot AE$)

In a circle angle at the centre is doubled the angle at the circumference subtended by the same arc.

$\angle AOC=2\angle AEC$

$\Rightarrow \angle AEC=\dfrac{1}{2}\times \angle AOC=\dfrac{{{90}^{\circ }}}{2}={{45}^{\circ }}$

ABCE is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$

$\angle ABC+\angle AEC={{180}^{\circ }}$

$\Rightarrow \angle ABC={{180}^{\circ }}-{{45}^{\circ }}={{135}^{\circ }}$

Similarly, $\angle CDE={{135}^{\circ }}$

$\angle ABC+\angle CDE={{135}^{\circ }}+{{135}^{\circ }}={{270}^{\circ }}$

Thus the value of $\angle ABC+\angle CDE$ is ${{270}^{\circ }}$.

46. In the given figure, AOC is a diameter and AC is parallel to ED. If $\angle CBE={{64}^{\circ }},$ Calculate $\angle DEC.$

Ans: Join the point AB.

In a circle angle subtended by the diameter at any point on the circumference is a right angle.

$\angle ABC={{90}^{\circ }}$

From the figure, $\angle ABE+\angle EBC={{90}^{\circ }}$

$\Rightarrow \angle ABE={{90}^{\circ }}-{{64}^{\circ }}={{26}^{\circ }}$

Angles subtended by the same arc on the circle are always equal.

$\angle ACE=\angle ABE={{26}^{\circ }}$

Since, AC||ED

$\angle ACE=\angle DEC$ (Alternate angles)

Therefore, $\angle DEC={{26}^{\circ }}$

Thus the value of $\angle DEC$ is ${{26}^{\circ }}$.

47. Use the given figure to find :

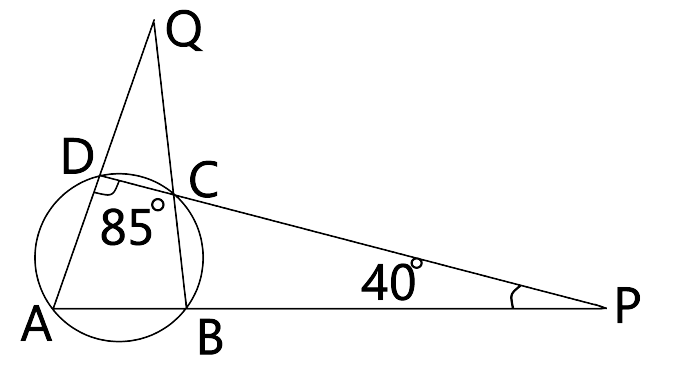
(i).$\angle BAD$

Ans: By the angle sum property the sum of all interior angles in a triangle is ${{180}^{\circ }}$.

In $\Delta APD$By using angle sum property,

$\angle ADP+\angle APD+\angle PAD={{180}^{\circ }}$

$\Rightarrow \angle PAD={{180}^{\circ }}-{{85}^{\circ }}-{{40}^{\circ }}={{55}^{\circ }}$

$\angle BAD=\angle PAD={{55}^{\circ }}$  (Angle b/w same line segments)

Thus the value of $\angle BAD$ is ${{55}^{\circ }}$.

(ii). $\angle DQB$

Ans: ABCD is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$

$\angle ADC+\angle ABC={{180}^{\circ }}$

$\Rightarrow \angle ABC={{180}^{\circ }}-{{85}^{\circ }}={{95}^{\circ }}$

Now by using angle sum property in $\Delta AQB$

$\angle QAB+\angle AQB+\angle ABQ={{180}^{\circ }}$

$\Rightarrow \angle AQB={{180}^{\circ }}-{{95}^{\circ }}-{{55}^{\circ }}={{30}^{\circ }}$

$\angle DQB=\angle AQB={{30}^{\circ }}$ (Angles b/w same line segments)

Thus the value of $\angle AQB$ is ${{30}^{\circ }}$.

48. In the given figure, AOB is a diameter and DC is parallel to AB. If $\angle CAB={{x}^{\circ }}$; find (in terms of x), the value of :

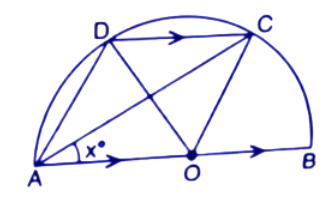
(i).$\angle COB$

Ans: In a circle, Angle at the centre is doubled the angle at the circumference subtended by the same arc. 

$\angle COB=2\angle CAB$

$\Rightarrow \angle COB=2{{x}^{\circ }}$ (∵ Given $\angle CAB={{x}^{\circ }}$)

Thus the value of $\angle COB$ is $2{{x}^{\circ }}$

(ii).$\angle DOC$

Ans: Since DC||AB

$\angle DCO=\angle COB$   (Alternate Angles)

Hence, $\angle DCO=2{{x}^{\circ }}$ 

OC=OD (Radii of circle)

$\angle ODC=\angle DCO=2{{x}^{\circ }}$ (opposite angles of equal sides are equal)

By using angle sum property in $\Delta ODC$

$\angle ODC+\angle DCO+\angle DOC={{180}^{\circ }}$

$\Rightarrow \angle DOC={{180}^{\circ }}-2{{x}^{\circ }}-2{{x}^{\circ }}=180-4{{x}^{\circ }}$

(iii). $\angle DAC$

Ans: In a circle, Angle at the centre is doubled the angle at circumference subtended by the same chord.

$\angle DOC=2\angle DAC$

$\Rightarrow \angle DAC=\dfrac{1}{2}{{\times }^{{}}}\angle DOC$

$\Rightarrow \angle DAC=\dfrac{1}{2}{{\times }^{{}}}\left( {{180}^{\circ }}-4{{x}^{\circ }} \right)={{90}^{\circ }}-2{{x}^{\circ }}$

Thus the value of $\angle DAC$ is ${{90}^{\circ }}-2{{x}^{\circ }}$.

(iv). $\angle ADC.$

Ans: Since, DC||AO

$\angle DCA=\angle CAO={{x}^{\circ }}$(Alternate angles)

$\angle DAC={{90}^{\circ }}-2{{x}^{\circ }}$ (From ii part)

By using angle sum property in $\Delta ADC$

$\angle DAC+\angle DCA+\angle ADC={{180}^{\circ }}$

$\Rightarrow \angle ADC={{180}^{\circ }}-\left( {{90}^{\circ }}-2{{x}^{\circ }} \right)-{{x}^{\circ }}={{90}^{\circ }}+{{x}^{\circ }}$

Thus the value of $\angle ADC$ is ${{90}^{\circ }}+{{x}^{\circ }}$.

49. In the given figure, AB is the diameter of a circle with centre O. $\angle BCD={{130}^{\circ }}$, Find:

(i). $\angle DAB$

Ans: ABCD is a cyclic quadrilateral. In a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$.

Hence,  $\angle DAB+\angle BCD={{180}^{\circ }}$

$\Rightarrow \angle DAB={{180}^{\circ }}-{{130}^{\circ }}={{50}^{\circ }}$

(ii). $\angle DBA$

Ans: In the given figure join BD.

In a circle angle subtended by the diameter at the circumference is right angle. Hence $\angle ADB={{90}^{\circ }}$.

By using the angle sum property in $\Delta ADB$

$\angle ADB+\angle DBA+\angle DAB={{180}^{\circ }}$

$\Rightarrow \angle DBA={{180}^{\circ }}-{{90}^{\circ }}-{{50}^{\circ }}={{40}^{\circ }}$ (∵ from (i) part $\angle DAB={{50}^{\circ }}$)

Thus the value of $\angle DBA$ is ${{40}^{\circ }}$.

50. In the given figure. PQ is the diameter of the circle whose centre is O. Given  $\angle ROS={{42}^{\circ }}$, calculate $\angle RTS.$

Ans: Join points RS and PS.

In a circle angle subtended by the diameter at circumference is right angle.

$\angle PSQ={{90}^{\circ }}$

In a circle angle at the centre is doubled the angle at the circumference subtended by the same chord.

$\angle ROS=2\angle SPR$

$\angle SPR=\dfrac{1}{2}\times {{42}^{\circ }}={{21}^{\circ }}$

$\angle SPR=\angle SPT$ (Angle b/w same line segment)

Therefore $\angle SPT={{21}^{\circ }}$

Now in $\Delta SPT$

$\angle SPT+\angle PTS+\angle PST={{180}^{\circ }}$

$\Rightarrow \angle PTS={{180}^{\circ }}-{{21}^{\circ }}-{{90}^{\circ }}={{69}^{\circ }}$ ($\angle PST={{90}^{\circ }}$ as $\angle PSQ={{90}^{\circ }}$)

Thus the value of $\angle PTS$ is ${{69}^{\circ }}$.

51. In the given figure, PQ is a diameter. Chord SR is parallel to PQ. Given that $\angle PQR={{58}^{\circ }},$ Calculate :

(i). $\angle RPQ$

Ans: Join Points PR

Angle subtended by the diameter on the circumference is the right angle.

$\angle PRQ={{90}^{\circ }}$

Now by using angle sum property in $\Delta PQR$.

$\angle PRQ+\angle PQR+\angle RPQ={{180}^{\circ }}$

$\Rightarrow \angle RPQ={{180}^{\circ }}-{{90}^{\circ }}-{{58}^{\circ }}={{180}^{\circ }}-{{148}^{\circ }}={{32}^{\circ }}$

Thus the value of $\angle RPQ$ is ${{32}^{\circ }}$.

(ii). $\angle STP.$

Ans: Since SR||PQ

$\angle SRP=\angle RPQ$ (Alternate angles)

∴$\angle SRP={{32}^{\circ }}$

STPR is a cyclic quadrilateral. In a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$.

$\angle STP+\angle SRP={{180}^{\circ }}$

$\Rightarrow \angle STP={{180}^{\circ }}-{{32}^{\circ }}={{148}^{\circ }}$

Thus the value of $\angle STP$ is ${{148}^{\circ }}$.

52. AB is the diameter of the circle with centre O. OD is parallel to BC and $\angle AOD={{60}^{\circ }}$. 

Calculate the numerical values of :

(i). $\angle ABD$

Ans: Join points BD.

Angle at the centre is doubled the angle at the circumference subtended by the same chord.

$\angle AOD=2\angle ABD$

$\Rightarrow \angle ABD=\dfrac{1}{2}\times \angle AOD=\dfrac{{{60}^{\circ }}}{2}={{30}^{\circ }}$

Thus the value of $\angle ABD$ is ${{30}^{\circ }}$.

(ii). $\angle DBC$

Ans: AOB is a straight line.

$\angle AOD+\angle BOD={{180}^{\circ }}$

$\Rightarrow \angle BOD={{180}^{\circ }}-{{60}^{\circ }}={{120}^{\circ }}$

Now in$\Delta BOD$ by using angle sum property,

$\angle BOD+\angle ODB+\angle OBD={{180}^{\circ }}$

$\Rightarrow \angle ODB={{180}^{\circ }}-{{120}^{\circ }}-{{30}^{\circ }}={{30}^{\circ }}$

Since OD||BC

$\angle ODB=\angle DBC$  (Alternate angles)

∴$\angle DBC={{30}^{\circ }}$

Thus the value of $\angle DBC$is ${{30}^{\circ }}$.

(iii). $\angle ADC.$

Ans: ABCD is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$.

$\angle ABC+\angle ADC={{180}^{\circ }}$

$\because \angle ABC=\angle ABD+\angle DBC={{30}^{\circ }}+{{30}^{\circ }}={{60}^{\circ }}$

Now, $\angle ABC+\angle ADC={{180}^{\circ }}$

$\Rightarrow \angle ADC={{180}^{\circ }}-{{60}^{\circ }}={{120}^{\circ }}$

Thus the value of $\angle ADC$ is ${{120}^{\circ }}$.

53. In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If $\angle APB={{75}^{\circ }}$and $\angle BCD={{40}^{\circ }},$ find :

(i). $\angle AOB$

Ans: Join points AB and AD.

In a circle, the angle at the centre is twice the angle at any point on circumference subtended by the same chord.

$\angle AOB=2\angle APB$

$\Rightarrow \angle AOB=2\times {{75}^{\circ }}={{150}^{\circ }}$

Thus the value of $\angle AOB$ is ${{150}^{\circ }}$.

(ii). $\angle ACB$

Ans: AOBC is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$.

$\angle AOB+\angle ACB={{180}^{\circ }}$

$\angle ACB={{180}^{\circ }}-{{150}^{\circ }}={{30}^{\circ }}$

Thus the value of $\angle ACB$ is ${{30}^{\circ }}$.

(iii). $\angle ABD$

Ans: Since $\angle ACD=\angle ACB+\angle BCD$

From (ii) part $\angle ACB={{30}^{\circ }}$ and given $\angle BCD={{40}^{\circ }}$

$\Rightarrow \angle ACD={{30}^{\circ }}+{{40}^{\circ }}={{70}^{\circ }}$

ABCD is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$.

$\angle ACD+\angle ABD={{180}^{\circ }}$

$\Rightarrow \angle ABD={{180}^{\circ }}-{{70}^{\circ }}={{110}^{\circ }}$

Thus the value of $\angle ABD$ is ${{110}^{\circ }}$

(iv). $\angle ADB$

Ans: OABD is a cyclic quadrilateral and  in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$.

$\angle ADB+\angle AOB={{180}^{\circ }}$

$\Rightarrow \angle ADB={{180}^{\circ }}-\angle AOB$

$\Rightarrow \angle ADB={{180}^{\circ }}-{{150}^{\circ }}={{30}^{\circ }}$

Thus the value of $\angle ADB$ is ${{30}^{\circ }}$.

54. In the given figure, $\angle BAD={{65}^{\circ }}$, $\angle ABD={{70}^{\circ }}$ and $\angle BDC={{45}^{\circ }},$ Find:

(i). $\angle BCD$

(ii). $\angle ACB$

Hence show that AC is a diameter.

(i). $\angle BCD$

Ans: ABCD is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$

$\angle BCD+\angle BAD={{180}^{\circ }}$

$\Rightarrow \angle BCD={{180}^{\circ }}-{{65}^{\circ }}={{115}^{\circ }}$

Thus the value of $\angle BCD$ is ${{115}^{\circ }}$.

(ii). $\angle ACB$

Hence show that AC is a diameter.

Ans: In $\Delta ABD$by using the angle sum property,

$\angle ADB+{{65}^{\circ }}+{{70}^{\circ }}={{180}^{\circ }}$

$\Rightarrow \angle ADB={{180}^{\circ }}-{{135}^{\circ }}={{45}^{\circ }}$

In a circle angles subtended by the same chord on the circumference are equal. Angles $\angle ADB$ and $\angle ACB$ are subtended by the same chord AB.

Hence, $\angle ACB=\angle ADB$

$\Rightarrow \angle ACB={{45}^{\circ }}$

Thus the value of $\angle ACB$ is ${{45}^{\circ }}$.

Since, $\angle ADC=\angle ADB+\angle BDC$

$\angle ADC={{45}^{\circ }}+{{45}^{\circ }}={{90}^{\circ }}$

$\angle ADC$ is right angle and subtended by AC. We know that an angle on the circumference is the right angle if it is subtended by the diameter. 

Thus AC is the diameter. 

55. In a cyclic quadrilateral ABCD, $\angle A:\angle C=3:1$and $\angle B:\angle D=1:5$; Find each angle of the quadrilateral.

Ans: Let the cyclic quadrilateral ABCD be as below:

and $\angle A=3x,~\angle C=x$

In a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$.

$\angle A+\angle C={{180}^{\circ }}$

$\Rightarrow 3x+x={{180}^{\circ }}$

$\Rightarrow x=\dfrac{{{180}^{\circ }}}{4}={{45}^{\circ }}$

Thus angles $\angle A=3\times {{45}^{\circ }}={{135}^{\circ }}$ and $\angle C=x={{45}^{\circ }}$

Now, Let $\angle B=y$ and $\angle D=5y$

$\angle B+\angle D={{180}^{\circ }}$

$\Rightarrow y+5y={{180}^{\circ }}$

$\Rightarrow y=\dfrac{{{180}^{\circ }}}{6}={{30}^{\circ }}$

Therefore angles $\angle B=y={{30}^{\circ }}$ and $\angle D=5y=5\times {{30}^{\circ }}={{150}^{\circ }}$.

56. The given figure shows a circle with centre O and $\angle ABP={{42}^{\circ }}.$

Calculate the measure of :

(i).$\angle PQB$

Ans: Join the points AP

In a circle Angle subtended by diameter at the circumference is the right angle.

$\angle APB={{90}^{\circ }}$

By using angle sum property in $\Delta APB$.

$\angle APB+\angle ABP+\angle PAB={{180}^{\circ }}$

$\Rightarrow \angle PAB={{180}^{\circ }}-{{90}^{\circ }}-{{42}^{\circ }}={{48}^{\circ }}$

In a circle, Angles at the circumference subtended by the same chord are always equal. Here $\angle PAB$ and $\angle PQB$ are subtended by the same chord PB.

∴ $\angle PQB=\angle PAB={{48}^{\circ }}$

Thus the value of $\angle PQB$ is ${{48}^{\circ }}$.

(ii). $\angle QPB+\angle PBQ$

By using angle sum property in $\Delta PQB$

$\angle QPB+\angle PBQ+\angle PQB={{180}^{\circ }}$

$\Rightarrow \angle QPB+\angle PBQ={{180}^{\circ }}-\angle PQB$

$\Rightarrow \angle QPB+\angle PBQ={{180}^{\circ }}-{{48}^{\circ }}={{132}^{\circ }}$

Thus the value of $\angle QPB+\angle PBQ$ is ${{132}^{\circ }}$.

57. In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other. If $\angle MAD=x$ and $\angle BAC=y$:

(i). Express $\angle AMD$in terms of x.     

Ans: AM=MD(Radii of circle)

Opposite angles of equal sides are always equal.

∴$\angle MAD=\angle MDA=x$

By using angle sum property in $\Delta AMD$ 

$\angle MAD+\angle MDA+\angle AMD={{180}^{\circ }}$

$\Rightarrow \angle AMD={{180}^{\circ }}-x-x={{180}^{\circ }}-2x$

Thus the value of $\angle AMD$ is ${{180}^{\circ }}-2x$.

(ii). Express $\angle ABD$in terms of y.

Ans: In a circle Angle at the centre is doubled the angle at the circumference subtended by the same chord.

$\angle AMD=2\angle ABD$

$\Rightarrow \angle ABD=\dfrac{1}{2}\times \angle AMD=\dfrac{1}{2}\times \left( {{180}^{\circ }}-2x \right)={{90}^{\circ }}-x$-------(1)

In $\Delta ALC$,

$\angle LAC+\angle ACL={{90}^{\circ }}$ 

$\angle ACL={{90}^{\circ }}-y$

$\angle ACL=\angle ACD$ (Angles b/w same line segments)

$\Rightarrow \angle ACD={{90}^{\circ }}-y$

In a circle angles subtended by the same chord at the circumference are always equal. 

$\angle ABD=\angle ACD$

$\angle ABD={{90}^{\circ }}-y$-----------(2)

Thus the value of $\angle ABD$ in terms of y is ${{90}^{\circ }}-y$.

(iii). Prove that: $x=y.$

From eq. (1) and (2).

${{90}^{\circ }}-x={{90}^{\circ }}-y$

$\Rightarrow x=y$

Hence proved.

Exercise-17B

1. In a cyclic trapezium, the non-parallel sides are equal and the diagonals are equal, Prove it.

Ans: 

ABCD is a cyclic trapezium and AB||CD

$\angle ABD=\angle BDC$ (Alternate angles)

In a circle, the angle at the centre is twice the angle at the circumference subtended by the same chord.

 $\angle AOD=2\angle ABD$  (Subtended by the chord AD)

And,  $\angle BOC=2\angle BDC$ (Subtended by the chord BC)

Since, $\angle ABD=\angle BDC$

$\therefore \angle AOD=\angle BOC$

We know that if the angles at the centre subtended by different chords are equal then the chords are equal to each other.

Since, $\angle AOD=\angle BOC$

$\Rightarrow $chord AD= chord BC

Therefore,  AD=BC

Now, In $\Delta ACD$ and $\Delta BDC$

DC=DC (Common side)

$\angle CAD=\angle CBD$ (Subtended by same chord CD)

AD=BC (Proved above)

Therefore, $\Delta ACD\Delta BDC$  (By S-A-S congruence criterion)

$\Rightarrow AC=BD$ (Hence proved)

2.  In the following figure, AD is the diameter of the circle with centre O. Chords AB, BC and CD are equal. If $\angle DEF={{110}^{\circ }}$, Calculate :

(i).$\angle AEF$

Ans: We Join points OB,OC and AE.

In a circle, Angle subtended by diameter at any point of the circumference is a right angle.

∴ $\angle AED={{90}^{\circ }}$

Given, $\angle DEF={{110}^{\circ }}$

$\angle AEF=\angle DEF-\angle AED={{110}^{\circ }}-{{90}^{\circ }}={{20}^{\circ }}$

$~~~~~~~~~~={{110}^{\circ }}-{{90}^{\circ }}={{20}^{\circ }}$

Thus the value of $\angle AEF$ is ${{20}^{\circ }}$.

(ii). $\angle FAB$

Ans: Given that Chord OA=OB=OC

Equal chords subtend the equal angles at the centre.

$\angle AOB=\angle BOC=\angle COD$

The sum of all angles on one side of a straight line is always ${{180}^{\circ }}$ . 

$\angle AOB+\angle BOC+\angle COD={{180}^{\circ }}$(AD is a straight line)

$\Rightarrow \angle AOB=\angle BOC=\angle COD={{60}^{\circ }}$

Since OA=OB (Radii of circle)

$\angle OAB=\angle OBA$(opposite angles of equal sides are equal to each other)

By using angle sum property in $\Delta AOB$

$\angle OAB+\angle OBA+\angle AOB={{180}^{\circ }}$

$\Rightarrow \angle OAB+\angle OAB={{180}^{\circ }}-{{60}^{\circ }}={{120}^{\circ }}$

$\Rightarrow \angle OAB=\dfrac{{{120}^{\circ }}}{2}={{60}^{\circ }}$

$\angle OAB=\angle OBA={{60}^{\circ }}$and $\angle AOB={{60}^{\circ }}$

Therefore, $\angle OAB=\angle OBA=\angle AOB={{60}^{\circ }}$

AFED is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$.

$\angle DAF+\angle FED={{180}^{\circ }}$

$\Rightarrow \angle DAF={{180}^{\circ }}-{{110}^{\circ }}={{70}^{\circ }}$

Now, From the figure:

$\angle FAB=\angle DAF+\angle OAB$

$\Rightarrow \angle FAB={{70}^{\circ }}+{{60}^{\circ }}={{130}^{\circ }}$

Thus the value of $\angle FAB$ is ${{130}^{\circ }}$.

3. If two sides of a cyclic-quadrilateral are parallel; Prove that:

(i). Its other two sides are equal.

Ans: 

Let DC||AB

$\angle DCA=\angle CAB$(Alternate angles)

In a circle, Angle at the centre is twice the angle at the circumference subtended by the same chord.

$\angle DOA=2\angle DCA$  (Subtended by the chord DA)

$\angle BOC=2\angle CAB$ (Subtended by the chord BC)

Since $\angle DCA=\angle CAB$

∴$\angle DOA=\angle BOC$

By the circle theorem, We know that if angles at the centre subtended by the different chords are equal then chords are equal to each other.

$\because ~\angle DOA=\angle BOC$

∴ chord AD=chord BC 

⇒AD=BC  (Hence proved)

(ii). Its diagonals are equal.

Ans: In $\Delta ABC$ and $\Delta ADB$

AB=AB (common side)

BC=AD (Proved in i part)

$\angle ACB$=$\angle ADB~$(Subtended by the same chord AB)

Therefore, $\Delta ABC\cong ~\Delta ADB$ (By the S-A-S criterion of congruence)

⇒ AC=BD (Hence proved)

4. The given figure shows a circle with centre O. Also, PQ=QR=RS and $\angle PTS={{75}^{\circ }}.~$ Calculate:

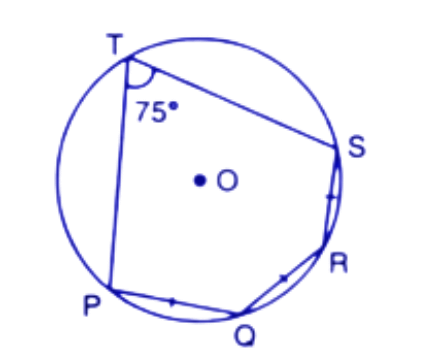
(i). $\angle POS$

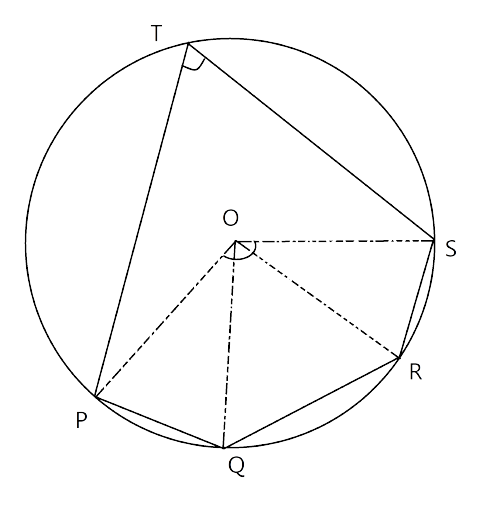
Ans: Join the lines OP, OQ , OQ and OS.

Given, PQ=QR=RS

Equal chords subtend the equal angles at centre.

$\angle POQ=\angle QOR=\angle SOR$

In a circle angle at the centre is doubled the angle at circumference subtended by the same arc.

$\angle POS=2\angle PTS$

$\angle POS=2\times {{75}^{\circ }}={{150}^{\circ }}$

Thus the value of $\angle POS$ is ${{150}^{\circ }}$.

(ii). $\angle QOR$

Ans: since $\angle POQ=\angle QOR=\angle SOR$

$\angle POQ+\angle QOR+\angle SOR=\angle POS$

$\angle POQ=\angle QOR=\angle SOR=\dfrac{{{150}^{\circ }}}{3}={{50}^{\circ }}$

Thus the value of $\angle QOR$is ${{50}^{\circ }}$

(iii). $\angle PQR$

Ans: In $\Delta POQ$

OP=OQ (Radii of circle)

∴ $\angle OPQ=\angle OQP$

Now, By using angle sum property.

$\angle OPQ+\angle OQP+\angle POQ={{180}^{\circ }}$

$\Rightarrow \angle OPQ+\angle OQP={{180}^{\circ }}-{{50}^{\circ }}={{130}^{\circ }}$

$\Rightarrow \angle OPQ=\angle OQP=\dfrac{{{130}^{\circ }}}{2}={{65}^{\circ }}$

Similarly in $\Delta QOR$

$\angle OQR=\angle ORQ={{65}^{\circ }}$

Now, $\angle PQR=\angle PQO+\angle OQR$

$\angle PQR={{65}^{\circ }}+{{65}^{\circ }}={{130}^{\circ }}$

Thus the value of $\angle PQR$ is ${{130}^{\circ }}$.

5. In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of :

(i). $\angle AOB$

Ans: AB is the a side of a regular six-sided 

polygon so this subtend the angle $=\dfrac{{{360}^{\circ }}}{6}={{60}^{\circ }}$

$\Rightarrow \angle AOB={{60}^{\circ }}$

(ii). $\angle ACB$

Ans: In a circle, Angle at the centre is twice the angle at any point of circumference subtended by the same chord. 

$\angle AOB=2\angle ACB$

$\Rightarrow \angle ACB=\dfrac{{{60}^{\circ }}}{2}={{30}^{\circ }}$

(iii). $\angle ABC$

Ans: 

Join the line OC.

AC is a side of a eight-sided regular polygon, So AB subtends the angle at centre as:

$\angle AOC=\dfrac{{{360}^{\circ }}}{8}={{45}^{\circ }}$.

In a circle, Angle at the centre is twice the angle at the circumference subtended by the same chord.

$\angle AOC=2\angle ABC$

$\Rightarrow \angle ABC=\dfrac{\angle AOC}{2}=\dfrac{{{45}^{\odot }}}{2}={{22.5}^{\circ }}$

Thus the value of $\angle ABC$ is ${{22.5}^{\circ }}$.

6. In a regular pentagon ABCDE, inscribed in a circle; find the ratio between angle EDA and angle ADC.

Ans: 

ABCDE is regular pentagon and each side subtends the angle at centre as:

$\dfrac{{{360}^{\circ }}}{5}={{72}^{\circ }}$.

So the angles $\angle AOE=\angle AOB=\angle BOC=\angle COD=\angle DOE={{72}^{\circ }}$.

In a circle, Angle at the centre is twice the angle at circumference subtended by the same chord.

$\angle AOE=2\angle EDA$  (subtended by the chord AE)

$\Rightarrow \angle EDA=\dfrac{\angle AOE}{2}=\dfrac{{{72}^{\circ }}}{2}={{36}^{\circ }}$

Similarly, $\angle ADB={{36}^{\circ }}$ and $\angle BDC={{36}^{\circ }}$

From the figure, $\angle ADC=\angle ADB+\angle BDC$

$\Rightarrow \angle ADC=\angle ADB+\angle BDC={{36}^{\circ }}+{{36}^{\circ }}={{72}^{\circ }}$

Now, $\angle EDA:\angle ADC={{36}^{\circ }}:{{72}^{\circ }}=1:2$

Thus the ratio is $1:2$.

7. In the given figure, AB=BC=CD and $\angle ABC={{132}^{\circ }}$. Calculate:

(i). $\angle AEB$

Ans: Join points EB and EC

ABCE is cyclic quadrilateral and in  ac cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$

$\angle AEC+\angle ABC={{180}^{\circ }}$

$\Rightarrow \angle AEC={{180}^{\circ }}-{{132}^{\circ }}={{48}^{\circ }}$  (Given, $\angle ABC={{132}^{\circ }}$)

Given, chord AB= chord BC. So, they will subtend the same angle.

$\angle AEB=\angle BEC$

And, $\angle AEC=\angle AEB+\angle BEC$

$\Rightarrow \angle AEB=\dfrac{\angle AEC}{2}=\dfrac{{{48}^{\circ }}}{2}={{24}^{\circ }}$

Thus the value of $\angle AEB$ is ${{24}^{\circ }}$.

(ii). $\angle AED$

Ans: Since, AB=BC=CD

Equal chords subtend the equal angles.

Hence, $\angle AEB=\angle BEC=\angle CED={{24}^{\circ }}$  (From (i) part $\angle AEB={{24}^{\circ }}$)

And, $\angle AED=\angle AEB+\angle BEC+\angle CED$

$\Rightarrow \angle AED={{24}^{\circ }}+{{24}^{\circ }}+{{24}^{\circ }}={{72}^{\circ }}$

Thus the value of $\angle AED$ is ${{72}^{\circ }}$.

(iii).$\angle COD$

Ans: In a circle, Angle at the centre is twice the angle at the circumference subtended by the same chord. Here angles $\angle COD~\text{and}~2\angle CED$ are subtended by chord CD.

$\angle COD=2\angle CED$

$\Rightarrow \angle COD=2\times {{24}^{\circ }}={{48}^{\circ }}$

Thus the value of $\angle COD$ is ${{48}^{\circ }}$.

8. In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle $AOB={{108}^{\circ }},$ find:

(i). $\angle CAB$

Ans: Join AD and BD.

Given, arc AB= 2 arc BC

Therefore, $\angle AOB=2\angle BOC$

$\Rightarrow \angle BOC=\dfrac{{{108}^{\circ }}}{2}={{54}^{\circ }}$

In a circle angle at the centre is doubled the angle at the circumference subtended by the same chord. Here $\angle BOC$ angle at the centre and $\angle CAB$ angle at the circumference both are subtended by the chord BC. 

So, $\angle BOC=2\angle CAB$

$\Rightarrow \angle CAB=\dfrac{1}{2}\times {{54}^{\circ }}={{27}^{\circ }}$

Thus the value of $\angle CAB$ is ${{27}^{\circ }}$

(ii). $\angle ADB$

Ans: In a circle angle at the centre is doubled the angle at the circumference 

Subtended by the same chord.

 $\angle AOB=2\angle ACB$

$\Rightarrow \angle ACB=\dfrac{{{108}^{\circ }}}{2}={{54}^{\circ }}$

ABCD is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$

$\angle ADB+\angle ACB={{180}^{\circ }}$

$\Rightarrow \angle ADB={{180}^{\circ }}-{{54}^{\circ }}={{126}^{\circ }}$

Thus the value of $\angle ADB$ is ${{126}^{\circ }}$.

9. The figure shows a circle with centre O. AB is the side of the rectangular pentagon and AC is the side of the regular hexagon. Find the angles of triangle ABC.

Ans: Join the points OA, OB and OC

Given that AB is a side of regular pentagon and we know that each side of pentagon inscribed in a circle subtends the angle of measure $=\dfrac{{{360}^{\circ }}}{5}={{72}^{\circ }}$

Thus the angle AOB subtended by chord AB=${{72}^{\circ }}$

AC is a side of regular hexagon and we know that each side of hexagon inscribed in a circle subtends the angle of measure $=\dfrac{{{360}^{\circ }}}{6}={{60}^{\circ }}$

Thus the angle AOC subtended by chord AC=${{60}^{\circ }}$.

In a circle, Angle at the centre is doubled the angle at the circumference subtended by the same chord.

$\angle AOC=2\angle ABC$ (Subtended by chord AC)

$\Rightarrow \angle ABC=\dfrac{{{60}^{\circ }}}{2}={{30}^{\circ }}$

And, $\angle AOB=2\angle ACB$ (Subtended by chord AB)

$\Rightarrow \angle ACB=\dfrac{\angle AOB}{2}=\dfrac{{{72}^{\circ }}}{2}={{36}^{\circ }}$

By using angle sum property in $\Delta ABC$

$\angle ABC+\angle ACB+\angle BAC={{180}^{\circ }}$

$\Rightarrow \angle BAC={{180}^{\circ }}-{{30}^{\circ }}-{{36}^{\circ }}={{114}^{\circ }}$

Thus the value of angles of $\Delta ABC$ are ${{30}^{\circ }},~{{36}^{\circ }},{{114}^{\circ }}.~$

10. In the given figure, BD is a side of a regular hexagon, DC is a side of a regular pentagon and AD is a diameter. Calculate :

Ans: Join the points CO, EO, BC and BO.

(i). $\angle ADC$

Ans: Since, BD is a side of regular hexagon, hence it subtends the angle at centre as:

$\angle BOD=\dfrac{{{360}^{\circ }}}{6}={{60}^{\circ }}$

Similarly, CD is a side of regular pentagon, hence it subtends the angle at centre as:

$\angle COD=\dfrac{{{360}^{\circ }}}{5}={{72}^{\circ }}$

In $\Delta BOD$

$\angle BOD={{60}^{\circ }}$ and OB=OD (Radii of circle)

$\therefore \angle BDO=\angle OBD={{60}^{\circ }}$

And, In $\Delta COD$

OC=OD (Radii of circle)

$\therefore \angle CDO=\angle OCD$ (Alternate angles)

$\angle CDO+\angle OCD+\angle COD={{180}^{\circ }}$

$\Rightarrow 2\angle CDO={{180}^{\circ }}-{{72}^{\circ }}={{108}^{\circ }}$

$\Rightarrow \angle CDO={{54}^{\circ }}$

$\angle ADC=\angle CDO={{54}^{\circ }}$ (Angles b/w same line segments)

Thus the value of $\angle ADC$ is ${{54}^{\circ }}$.

(ii). $\angle BDA$

Ans: From (i) part $\angle BDO={{60}^{\circ }}$

$\angle BDA=\angle BDO={{60}^{\circ }}$ (Angles b/w same line segments)

(iii). $\angle ABC$

Ans: In a circle, Angle at the centre is doubled the angle at circumference subtended by the same chord.

$\angle AOC=2\angle ABC$

$\Rightarrow \angle ABC=\dfrac{1}{2}\times \angle AOC$

$\Rightarrow \angle ABC=\dfrac{1}{2}\times \left( \angle AOD-\angle COD \right)$

$\Rightarrow \angle ABC=\dfrac{1}{2}\times \left( {{180}^{\circ }}-{{72}^{\circ }} \right)$

$\Rightarrow \angle ABC=\dfrac{1}{2}\times \left( {{108}^{\circ }} \right)={{54}^{\circ }}$

Thus the value of $\angle ABC$ is ${{54}^{\circ }}$

(iv). $\angle AEC$

Ans: $\angle AEC+\angle ADC={{180}^{\circ }}$

$\Rightarrow \angle AEC={{180}^{\circ }}-\angle ADC$

$\Rightarrow \angle AEC={{180}^{\circ }}-{{54}^{\circ }}={{126}^{\circ }}$ (From (i) part $\angle ADC={{54}^{\circ }}$)

Thus the value of $\angle AEC$ is ${{126}^{\circ }}$.

Exercise-17(C)

1. In the given circle with diameter AB, find the value of x.

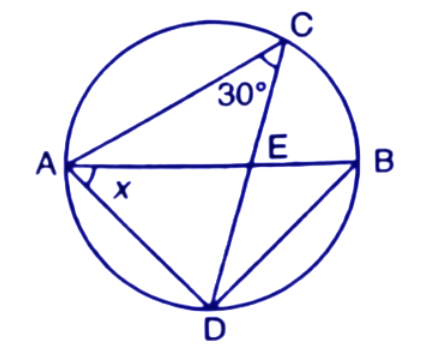
Ans: In a circle, Angles at the circumference subtended by the same chord are equal.

$\angle ABD=\angle ACD={{30}^{\circ }}$ (From the figure $\angle ACD={{30}^{\circ }}$)

The angle on the circumference subtended by the diameter is a right angle. 

$\angle ADB={{90}^{\circ }}$

Now, By using the angle sum property in $\Delta ABD$

$\angle ABD+\angle ADB+\angle BAD={{180}^{\circ }}$

$\Rightarrow \angle BAD={{180}^{\circ }}-{{30}^{\circ }}-{{90}^{\circ }}={{60}^{\circ }}$

$\Rightarrow x={{60}^{\circ }}$ (From the figure $\angle BAD=x$)

Thus the value of $x$ is ${{60}^{\circ }}$.

2. In the given figure, ABC is a triangle in which $\angle BAC={{30}^{\circ }}$. Show that BC is equal to the radius of the circumcircle of the triangle ABC, whose centre is O.

Ans: Join the points OB, OC.

In a circle, Angle at the centre is doubled the angle at the circumference subtended by the same chord.

$\angle BOC=2\angle BAC$

$\Rightarrow \angle BOC=2\times {{30}^{\circ }}={{60}^{\circ }}$

Since, OB=OC (Radii of same circle)

$\angle OBC=\angle OCB$ (Angles opposite to equal sides are equal)

Now, by using the angle sum property in $\Delta OBC$

$\angle OBC+\angle OCB+\angle BOC={{180}^{\circ }}$

$\Rightarrow \angle OBC+\angle OCB={{180}^{\circ }}-{{60}^{\circ }}={{120}^{\circ }}$

$\Rightarrow 2\angle OBC={{120}^{\circ }}$

$\Rightarrow \angle OBC=\dfrac{{{120}^{\circ }}}{2}={{60}^{\circ }}$

Thus, $\angle OBC=\angle OCB=\angle BOC={{60}^{\circ }}$

Therefore $\Delta OBC$ is an equilateral triangle.

Hence, OB=OC=BC.

So, BC is equal to the radius of the circumcircle of the triangle ABC.

3. Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.

Ans: 

Given AB is a diameter.

In a circle angle subtended by diameter is a right angle. $\angle ADB~$ is subtended by AB. 

SO, $\angle ADB={{90}^{\circ }}$

BC is a straight line and the sum of angles on a straight line is ${{180}^{\circ }}$.

$\angle ADB+\angle ADC={{180}^{\circ }}$

$\Rightarrow \angle ADC={{180}^{\circ }}-{{90}^{\circ }}={{90}^{\circ }}$

Now, In $\Delta ADB$ and $\Delta ADC$

AD=AD (Common side)

AB=AC (Given)

$\angle ADB=\angle ADC$ (Proved)

$\Delta ABD~\cong ~\Delta ADC$

Therefore, BD=DC

Thus D is a midpoint of BC.

4. In the given figure, chord ED is parallel to diameter AC of the circle. Given $\angle CBE={{65}^{\circ }}$, calculate $\angle DEC$.

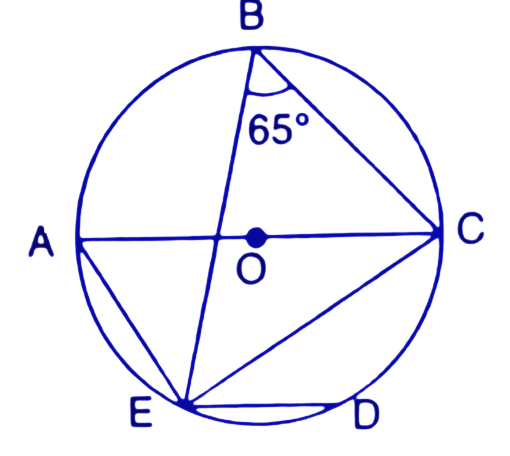
Ans: Join the points AB, EO and DC.

In a circle, Angle at the centre is doubled, the angle subtended by the same chord.

$\angle COE=2\angle CBE$

$\Rightarrow \angle COE=2\times {{65}^{\circ }}={{130}^{\circ }}$

Since, OE=OC (Radii of same circle)

$\angle OEC=\angle OCE$

Now, In $\Delta COE$

$\angle OEC+\angle OCE+\angle COE={{180}^{\circ }}$

$\Rightarrow 2\angle OCE={{180}^{\circ }}-{{130}^{\circ }}={{50}^{\circ }}$

$\Rightarrow \angle OCE=\dfrac{{{50}^{\circ }}}{2}={{25}^{\circ }}$

Hence, $\angle OCE=\angle OEC={{25}^{\circ }}$

Given, ED||AC

$\angle DEC=\angle OCE$ (Alternate angles)

Therefore, $\angle DEC={{25}^{\circ }}$

Thus the value of $\angle DEC$ is ${{25}^{\circ }}$.

5. The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.

Ans: 

In $\Delta APD$

$\angle PDA+\angle PAD+\angle APD={{180}^{\circ }}$  -----------(1)

In $\Delta BQC$

$\angle BQC+\angle QCB+\angle QBC={{180}^{\circ }}$ --------(2)

By adding eq. (1) and (2)

$\angle PDA+\angle PAD+\angle APD+\angle BQC+\angle QCB+\angle QBC={{360}^{\circ }}$------(3)

Since AP, BQ, CQ and DP are angle bisectors of $\angle A,~\angle B,~\angle C~and~\angle D$ respectively.

Therefore, $\angle PDA=\dfrac{1}{2}\times \angle D$-------(4)

$\angle PAD=\dfrac{1}{2}\times \angle A$-------(5)

$\angle QBC=\dfrac{1}{2}\times \angle B$-------(6)

$\angle QCB=\dfrac{1}{2}\times \angle C$------(7)

By adding Eq. (4), (5), (6) and (7)

$\angle PDA+\angle PAD+\angle QBC+\angle QCB=\dfrac{1}{2}\left( \angle A+\angle B+\angle C+\angle D \right)$----(8)

Now by putting this value from eq. (8) in eq. (3)

$\angle APD+\angle BQC={{360}^{\circ }}-\dfrac{1}{2}\left( \angle A+\angle B+\angle C+\angle D \right)$

We know that the sum of all interior of a quadrilateral is ${{360}^{\circ }}$

$\angle APD+\angle BQC={{360}^{\circ }}-\dfrac{1}{2}\left( {{360}^{\circ }} \right)={{180}^{\circ }}$

$\angle APD~\And ~\angle BQC$ are opposite angles of quadrilateral PSQR. If the sum of opposite angles of a quadrilateral inscribed in a circle is ${{180}^{\circ }}$ then the quadrilateral is cyclic quadrilateral. 

Thus PSQR is a cyclic quadrilateral.

6. In the figure, $\angle DBC={{58}^{\circ }}$. BD is the diameter of the circle. Calculate:

(i). $\angle BDC$

Ans: In a circle, Angle at the circumference subtended by the diameter is the right angle. 

$\angle BCD={{90}^{\circ }}$

Now by using angle sum property in $\Delta BCD$

$\angle BCD+\angle DBC+\angle BDC={{180}^{\circ }}$

$\Rightarrow \angle BDC={{180}^{\circ }}-{{90}^{\circ }}-{{58}^{\circ }}={{32}^{\circ }}$

Thus the value of $\angle BDC$ is ${{32}^{\circ }}$.

(ii). $\angle BEC$

Ans: BECD is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$

$\angle BEC+\angle BDC={{180}^{\circ }}$

$\Rightarrow \angle BEC={{180}^{\circ }}-{{32}^{\circ }}={{148}^{\circ }}$

Thus the value of $\angle BEC$ is ${{148}^{\circ }}$.

(iii). $\angle BAC$

Ans: In a circle, Angles at the circumference subtended by the same chord are equal.

$\angle BAC=\angle BDC$ (Subtended by chord BC)

Therefore, $\angle BAC={{32}^{\circ }}$ (from (ii)part $\angle BDC={{32}^{\circ }}$)

7. D and E are points on equal sides AB andAC of an isosceles triangle ABC such that AD=AE. Prove that the points B, C, E and D are concyclic.

Ans: 

Given, AB=AC

$\Rightarrow \angle B=\angle C$

And, AD=AE

$\angle ADE=\angle AED$

In $\Delta ABC$

$\dfrac{AD}{AB}=\dfrac{AE}{AC}$

Therefore, DE||BC

$\therefore \angle ADE=\angle B$ (Corresponding angles) -------(1)

And, $\angle B=\angle C$(Proved) -------(2)

From eq. (1) and (2)

$\angle ADE=\angle C$

$\angle ADE$ is exterior angle of quadrilateral BCED and we know that if the exterior angle of a quadrilateral inscribed in a circle is equal to the opposite interior angle then the quadrilateral is cyclic quadrilateral.

Thus BCDE is a cyclic quadrilateral. Hence, B,C,D and E are concyclic points.

8. In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If $\angle ADC={{92}^{\circ }}$, $\angle FAE={{20}^{\circ }}$;determine $\angle BCD$. Give reason in support of your answer. 

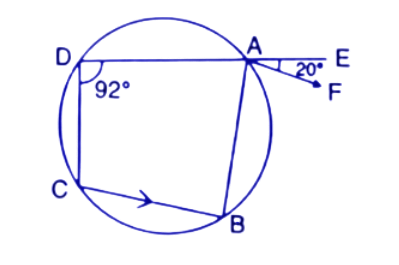
Ans: Given, ABCD is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$

$\angle ADC+\angle ABC={{180}^{\circ }}$

$\Rightarrow \angle ABC={{180}^{\circ }}-{{92}^{\circ }}={{88}^{\circ }}$

Since, AF||BC

$\angle FAB=\angle ABC={{88}^{\circ }}$ (Alternate angle)

Now, $\angle BAE=\angle BAF+\angle FAE$

$\Rightarrow \angle BAE={{88}^{\circ }}+{{22}^{\circ }}={{110}^{\circ }}$

In a cyclic quadrilateral the exterior angle is equal to the interior opposite angle. 

$\angle BCD=\angle BAE={{110}^{\circ }}$

Thus the value of $\angle BCD$ is ${{110}^{\circ }}$.

9. If I is  the incentre of triangle ABC and AI when produced meets the circumcircle of triangle ABC in point D. If $\angle BAC={{66}^{\circ }}$ and $\angle ABC={{80}^{\circ }}$, Calculate: 

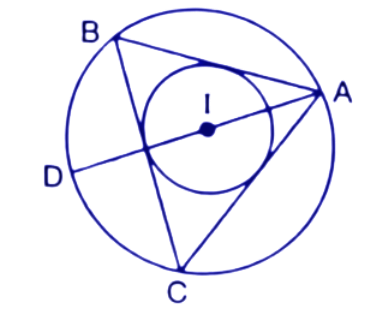
Ans: 

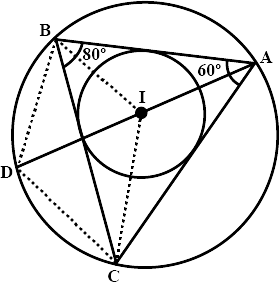
Join the points BD, CD, IB and IC.

(i). $\angle DBC$

Ans: IA is angle bisector. So, $\angle BAD=\angle CAD$

$\angle BAC={{66}^{\circ }}$

$\Rightarrow \angle BAD+\angle CAD={{66}^{\circ }}$

$\Rightarrow 2\angle CAD={{66}^{\circ }}$

$\Rightarrow \angle CAD={{33}^{\circ }}$

In a circle, Angles subtended by the same chord at the circumference are always equal.

$\angle DBC=\angle CAD$ (Subtended by chord CD)

$\Rightarrow \angle DBC={{33}^{\circ }}$

Thus the value of $\angle DBC$ is ${{33}^{\circ }}$.

(ii). $\angle IBC$

Ans: IB is an angle bisector. So, $\angle IBC=\angle IBC=\angle IBA$

$\angle IBC=\angle IBA=\dfrac{\angle ABC}{2}=\dfrac{{{80}^{\circ }}}{2}={{40}^{\circ }}$

Thus the value of $\angle IBC$ is ${{40}^{\circ }}$.

(iii). $\angle BIC$

Ans: By using angle sum property in $\Delta ABC$

$\angle ABC+\angle ACB+\angle BAC={{180}^{\circ }}$

$\Rightarrow \angle ACB={{180}^{\circ }}-{{80}^{\circ }}-{{66}^{\circ }}={{34}^{\circ }}$

IC is an angle bisector of $\angle ACB$ . So, $\angle BCI=\angle ACI$

$\angle BCI=\angle ACI=\dfrac{{{34}^{\circ }}}{2}={{17}^{\circ }}$

Now, By using angle sum property in $\Delta BIC$

$\angle BCI+\angle BIC+\angle IBC={{180}^{\circ }}$

$\Rightarrow \angle BIC={{180}^{\circ }}-{{17}^{\circ }}-{{40}^{\circ }}={{123}^{\circ }}$

Thus the value of $\angle BIC$ is ${{123}^{\circ }}$.

10. In the given figure, AB=AD=DC=PB and $\angle DBC={{x}^{\circ }}$. Determine, in terms of x :

(i). $\angle ABD$

Ans: Join the points AC and BD.

In a circle, Angles subtended by the same chord at the circumference are always equal.

$\angle DBC=\angle DAC$ (Subtended by chord DC)

$\angle DCA=\angle DAC$ (AD=DC)

$\angle ABD=\angle DCA$ (Subtended by chord AD)

Therefore, $\angle ABD=\angle DBC={{x}^{\circ }}$ (Given $\angle DBC={{x}^{\circ }}$)

Thus the value of $\angle ABD$ is ${{x}^{\circ }}$.

(ii). $\angle APB$

Hence or otherwise, prove that AP is parallel to DB.

Ans: Since, AB=PB

$\angle BAP=\angle APB$

In $\Delta ABP$, $\angle ABC$ is the exterior angle.

We know that the exterior angle is equal to the sum of opposite angles.

$\angle ABC=\angle BAP+\angle APB$

$\Rightarrow 2x~=~2\angle APB$

$\Rightarrow \angle APB=x$

Thus the value of $\angle APB$ is $x$.

Since, $\angle APB=\angle DBC={{x}^{\circ }}$

These are corresponding angles and we know that if two corresponding angles are equal the sides are also equal.

Therefore AP||DB.

11. In the given figure: ABC, AEQ and CEP are straight lines. Show that $\angle APE$ and $\angle CQE$ are supplementary.

Ans: Join the line EB.

In a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$

ABEP is a cyclic quadrilateral. Hence,

$\angle APE+\angle ABE={{180}^{\circ }}$--------(1)

BEQC is a cyclic quadrilateral. Hence,

$\angle CQE+\angle CBE={{180}^{\circ }}$--------(2)

On adding eq. (1) and (2)

$\angle APE+\angle ABE+\angle CQE+\angle CBE={{360}^{\circ }}$

$\Rightarrow \angle APE+\angle CQE={{360}^{\circ }}-\left( \angle ABE+\angle CBE \right)$

$\Rightarrow \angle APE+\angle CQE={{360}^{\circ }}-{{180}^{\circ }}={{180}^{\circ }}$ ($\angle ABE+\angle CBE$ linear pair)

Thus, $\angle APE$ and $\angle CQE$ are supplementary.

12. In the given figure, AB is the diameter of the circle with centre O. If $\angle ADC={{32}^{\circ }}$, find angle BOC.

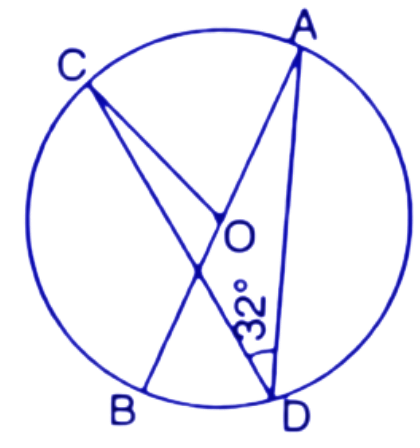
Ans: In a circle, The angle at the centre is doubled at the circumference subtended by the same chord. 

$\angle AOC=2\angle ADC=2\times {{32}^{\circ }}={{64}^{\circ }}$

Since, $\angle AOC$ and $\angle BOC$ are linear pairs. Therefore,

$\angle AOC+\angle BOC={{180}^{\circ }}$

$\Rightarrow \angle BOC={{180}^{\circ }}-{{64}^{\circ }}={{116}^{\circ }}$

Thus the value of $\angle BOC$ is ${{116}^{\circ }}$.

13. In a cyclic-quadrilateral PQRS, angle $\angle PQR={{135}^{\circ }},$ Sides SP and RQ produced meet at point A whereas sides PQ and SR produced meet at point B.

If $\angle A:\angle B=2:1$; find angles A and B.

Ans: 

Let $\angle A=2x$ and $\angle B=x$

PQRS is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$

$\angle PQR+\angle S={{180}^{\circ }}$

$\Rightarrow \angle S={{180}^{\circ }}-{{135}^{\circ }}={{45}^{\circ }}$

AQR is a straight line and the sum of angles on a straight line is ${{180}^{\circ }}$.

$\angle PQR+\angle PQA={{180}^{\circ }}$

$\Rightarrow \angle PQA={{180}^{\circ }}-{{135}^{\circ }}={{45}^{\circ }}$

By using angle sum property in $\Delta PBS$

$\angle S+\angle P+x={{180}^{\circ }}$

$\Rightarrow \angle P={{180}^{\circ }}-{{45}^{\circ }}-x={{135}^{\circ }}-x$--------(1)

Now by using exterior angle property in $\Delta PQA$, $\angle P$ is exterior angle

$\angle P=\angle PQA+\angle A={{45}^{\circ }}+2x$------(2)

From eq. (1) and (2)

${{45}^{\circ }}+2x={{135}^{\circ }}-x$

$\Rightarrow 3x={{90}^{\circ }}$

$\Rightarrow x={{30}^{\circ }}$

Therefore the angle $\angle A=2x=2\times {{30}^{\circ }}={{60}^{\circ }}$ and $\angle B=x={{30}^{\circ }}$.

14. In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC. 

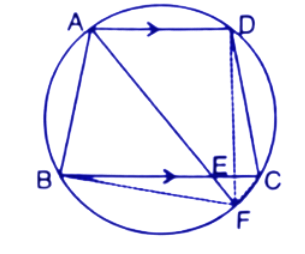
If the bisector of angle A meets BC at point E and the given circle at point F, prove that:

(i). EF=FC

Ans: AF is angle bisector of angle $\angle DAB$

Hence, $\angle DAF=\angle BAF$

Also, $\angle DAE=\angle BAE$-----(1)

∵ AD||BC

∴$\angle DAE=\angle AEB$ (Alternate angles)-----(2)

From eq. (1) and (2)

$\angle BAE=\angle AEB$

In $\Delta AEB$ By using angle sum property,

$\angle BAE+\angle AEB+\angle ABE={{180}^{\circ }}$

$\angle ABE={{180}^{\circ }}-2\angle AEB$ (∵$\angle BAE=\angle AEB$)

$\angle CEF=\angle AEB$(Vertically opposite angles)

ABCD is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$.

$\angle ABC+\angle ADC={{180}^{\circ }}$

$\Rightarrow \angle ADC={{180}^{\circ }}-\angle ABC$

$\Rightarrow \angle ADC={{180}^{\circ }}-\angle ABE$ ($\angle ABE$ and $\angle ABC$angles are b/w same line segments )

$\Rightarrow \angle ADC={{180}^{\circ }}-\left( {{180}^{\circ }}-2\angle AEB \right)=2\angle AEB$

Also, ADCF is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$.

$\angle ADC+\angle AFC={{180}^{\circ }}$

$\angle AFC={{180}^{\circ }}-\angle ADC={{180}^{\circ }}-2\angle AEB$

By using angle sum property in $\Delta EFC$

$\angle EFC+\angle ECF+\angle FEC={{180}^{\circ }}$

$\Rightarrow \angle ECF={{180}^{\circ }}-\angle CEF-\angle AFC$   ($\angle AFC=\angle EFC$ ∵angles b/w same line segment)

since, $\angle CEF=\angle AEB$ (Vertically opposite angles)

and $\angle AFC={{180}^{\circ }}-2\angle AEB$

$\Rightarrow \angle ECF={{180}^{\circ }}-\left( {{180}^{\circ }}-2\angle AEB \right)-\angle AEB$ 

$\Rightarrow \angle ECF=\angle AEB$-----(3)

And, $\angle CEF=\angle AEB$-----(4)

From eq.(3) and (4)

$\angle ECF=\angle CEF$

If in a triangle two angles are equal then the opposite sides of them are also equal.

∴ EF=FC 

(ii). BF=DF

Ans: Since AF is angle bisector of $\angle DAB$

∴$\angle DAF=\angle BAF$

Angle $\angle DAE$is subtended by chord DF and $\angle BAF$ is subtended by chord BF. If angles at the circumference subtended by the different chords are equal then the chords are also equal.

So, Chord BF= Chord DF

⇒ BF=DF 

15. ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F.

If $\angle DCF:\angle F:\angle E=3:5:4$, find the angles of the cyclic quadrilateral ABCD.

Ans: 

Let $\angle DCF=3x,~\angle F=5x$and $\angle E=4x$

BCF is a straight line.

$\angle DCF+\angle DCB={{180}^{\circ }}$(linear pair)

$\Rightarrow \angle DCB={{180}^{\circ }}-3x$

ABCD is a cyclic quadrilateral and the sum of opposite angles is ${{180}^{\circ }}$.

$\angle DCB+\angle A={{180}^{\circ }}$

$\Rightarrow \angle A={{180}^{\circ }}-\left( {{180}^{\circ }}-3x \right)=3x$

In $\Delta DCF$, $\angle CDA$ is the exterior angle. So by using the exterior angle property,

$\angle CDA=\angle F+\angle DCF=3x+5x=8x$

Since, $\angle BCE~\And ~\angle DCF$ are opposite angles.

So, $\angle BCE=\angle DCF=3x$

In $\Delta BCE$, 

Ext. $\angle ABC=\angle BCE+\angle E=3x+4x=7x$

ABCD is a cyclic quadrilateral and the sum of opposite angles is ${{180}^{\circ }}$.

$\angle CDA+\angle ABC={{180}^{\circ }}$

$\Rightarrow 7x+8x={{180}^{\circ }}$

$\Rightarrow x=\dfrac{{{180}^{\circ }}}{15}={{12}^{\circ }}$

Therefore the values of angles of a quadrilateral,

$\angle A=3x=3\times {{12}^{\circ }}={{36}^{\circ }}_{{}}$

$\angle B=\angle ABC=7x=7\times {{12}^{\circ }}={{84}^{\circ }}$

$\angle C=\angle DCB={{180}^{\circ }}-3x={{180}^{\circ }}-{{36}^{\circ }}={{144}^{\circ }}$

$\angle D=\angle CDA=8x=8\times {{12}^{\circ }}={{96}^{\circ }}$

16. The following figure shows a circle with PR as its diameter. If PQ=7cm and QR=3RS=6cm, find the perimeter of the cyclic quadrilateral PQRS.

Ans: Since, PQ=7cm and QR=3RS=6cm

So, $RS=\dfrac{6}{3}=2cm$, QR=6cm

$\angle PQR$is an angle made in semicircle.Hence $\Delta PQR$ is a right angle triangle.

Now by using pythagoras theorem,

$P{{R}^{2}}=P{{Q}^{2}}+Q{{R}^{2}}$

$\Rightarrow P{{R}^{2}}={{7}^{2}}+{{6}^{2}}=49+36=85$

Similarly, $\Delta PSR$

$P{{R}^{2}}=P{{S}^{2}}+S{{R}^{2}}$

$\Rightarrow 85=P{{S}^{2}}+4$

$\Rightarrow P{{S}^{2}}=81$

$\Rightarrow PS=9cm$

Therefore the perimeter of cyclic quadrilateral,

$PQ+QR+RS+PS=7+6+2+9=24cm$

17. In the figure, AB is the diameter of a circle with centre O. If chord AC=chord AD, prove that :

(i). Arc BC=arc DB

(ii). AB is bisector of $\angle CAD$.

Further, if the length of arc AC is twice the length of arc BC, find :

(a). $\angle BAC$

(b). $\angle ABC$

Ans: Join points BC and BD

(i). Arc BC=arc DB

Ans: In a circle, Angle subtended by the diameter at the circumference is a right angle. $\angle ACB$is subtended by diameter AB and similarly $\angle ADB\angle ACB$ is subtended by diameter AB.

$\angle ACB={{90}^{\circ }}$ and $\angle ADB={{90}^{\circ }}$

Therefore, $\angle ACB=\angle ADB={{90}^{\circ }}$

Now, In $\Delta ACB$ and $\angle ABD$

AB=AB (Common side)

AC=AD (Given)

$\angle ACB=\angle ADB={{90}^{\circ }}$(Proved above)

$\Delta ACB\Delta ABD$ (By SAS congruence criterion)

Therefore, BC=BD

(ii). AB is bisector of $\angle CAD$.

Ans: Since, $\Delta ACB\Delta ABD$

Therefore, $\angle BAC=\angle BAD$

So AB is a bisector of $\angle CAD$.

Further, if the length of arc AC is twice the length of arc BC, find :

(a). $\angle BAC$

Ans: If arc AC= 2 Arc BC

$\angle ABC=2\angle BAC$

Now by using the angle sum property in $\Delta ABC$

$\angle ABC+\angle BAC+\angle ACB={{180}^{\circ }}$

$\Rightarrow 3\angle BAC={{180}^{\circ }}-{{90}^{\circ }}={{90}^{\circ }}$

$\Rightarrow \angle BAC=\dfrac{{{90}^{\circ }}}{3}={{30}^{\circ }}$

(b). $\angle ABC$

Ans: Since, $\angle ABC=2\angle BAC$ and $\angle BAC={{30}^{\circ }}$

$\Rightarrow \angle ABC=2\times {{30}^{\circ }}={{60}^{\circ }}$

Therefore the value of $\angle ABC$ is ${{60}^{\circ }}$.

18. In cyclic quadrilateral ABCD; AD=BC, $\angle BAC={{30}^{\circ }}$ and $\angle CBD={{70}^{\circ }}$; find :

(i). $\angle BCD$

Ans: 

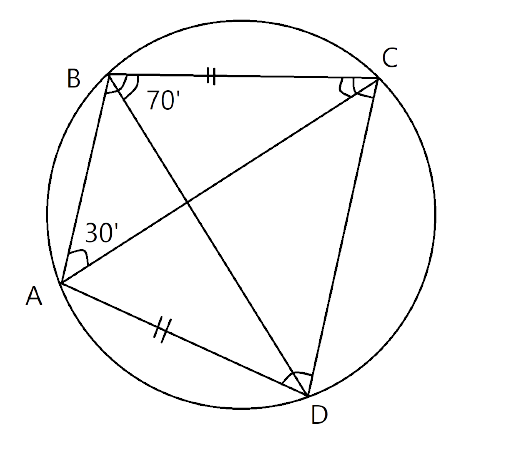
In a circle, the angles subtended by the same chord at the circumference are equal. Angles $\angle DBC$ and $\angle DAC$ are subtended by chord DC.

Hence, $\angle DAC=\angle DBC={{70}^{\circ }}$

$\angle BAD=\angle BAC+\angle DAC={{30}^{\circ }}+{{70}^{\circ }}={{100}^{\circ }}$

ABCD is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$.

$\angle BCD+\angle BAD={{180}^{\circ }}$

$\Rightarrow \angle BCD={{180}^{\circ }}-{{100}^{\circ }}={{80}^{\circ }}$

(ii). $\angle BCA$

Ans: By using angle sum property in $\Delta BCD$

$\angle BCD+\angle CDB+\angle BDC={{180}^{\circ }}$

$\Rightarrow \angle BDC={{180}^{\circ }}-{{80}^{\circ }}-{{70}^{\circ }}={{30}^{\circ }}$

Since, AD=BC

Therefore, $\angle ACD=\angle BDC={{30}^{\circ }}$

Since, $\angle BCA=\angle BCD-\angle ACD$

$\Rightarrow \angle BCA={{80}^{\circ }}-{{30}^{\circ }}={{50}^{\circ }}$

(iii). $\angle ABC$

Ans: In a circle, Angles at the circumference subtended by the same chord are always equal.

$\angle ABD=\angle ACD={{30}^{\circ }}$

So, $\angle ABC=\angle ABD+\angle CBD={{30}^{\circ }}+{{70}^{\circ }}={{100}^{\circ }}$

(iv). $\angle ADC$

Ans: ABCD is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$.

$\angle ADC+\angle ABC={{180}^{\circ }}$

$\Rightarrow \angle ADC={{180}^{\circ }}-{{100}^{\circ }}={{80}^{\circ }}$

19. In the given figure, $\angle ACE={{43}^{\circ }}$ and $\angle CAF={{62}^{\circ }}$; find the values of a, b and c.

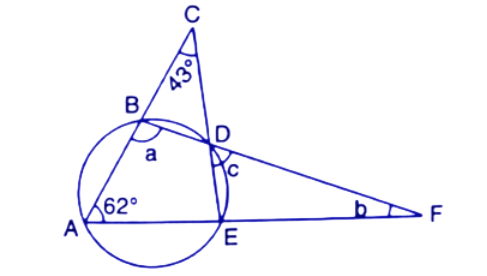
Ans: By using angle sum property in $\Delta ACE$

$\angle ACE+\angle AEC+\angle CAE={{180}^{\circ }}$

$\Rightarrow \angle AEC={{180}^{\circ }}-{{43}^{\circ }}-{{62}^{\circ }}={{75}^{\circ }}$

ABDE is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}.$

$\angle ABD+\angle AED={{180}^{\circ }}$

$\Rightarrow \angle ABD={{180}^{\circ }}-{{75}^{\circ }}={{105}^{\circ }}$

From figure, $\angle ABD=a={{105}^{\circ }}$

Thus the value of $a$ is ${{105}^{\circ }}$.

By using angle sum property in $\Delta BAF$

$a+b+{{62}^{\circ }}={{180}^{\circ }}$

$\Rightarrow b={{180}^{\circ }}-{{62}^{\circ }}-{{105}^{\circ }}={{13}^{\circ }}$

By using exterior angle property in $\Delta DEF$

Exterior $\angle DEA=c+b$

$\Rightarrow c=\angle CEA-b={{75}^{\circ }}-{{13}^{\circ }}={{62}^{\circ }}$ (∵ angle b/w same line segment $\angle CEA=\angle DEA$) 

Thus the values of $a={{105}^{\circ }},b={{13}^{\circ }}~$and $c={{62}^{\circ }}$.

20. In the given figure, AB is parallel to DC, $\angle BCE={{80}^{\circ }}$ and $\angle BAC={{25}^{\circ }}$.

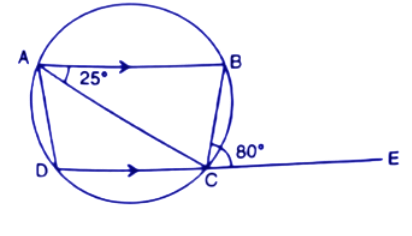
Find :

(i). $\angle CAD$

Ans: By exterior angle property, the exterior angle is equal to the opposite angle.
$\angle BAD=\angle BCE={{80}^{\circ }}$

Now, $\angle BAD=\angle BAC+\angle CAD$

$\Rightarrow \angle CAD={{80}^{\circ }}-{{25}^{\circ }}={{55}^{\circ }}$

(ii). $\angle CBD$

Ans: Join the points BD.

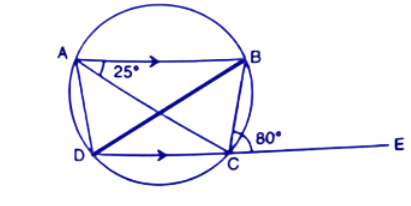
Angles at the circumference subtended by the same chord are always equal. 

Here $\angle CBD$ and $\angle CAD$ are subtended by chod DC.

$\angle CBD=\angle CAD$

From (i) part $\angle CAD={{55}^{\circ }}$

Therefore, $\angle CBD=\angle CAD={{55}^{\circ }}$

Thus the value of $\angle CBD$ is ${{55}^{\circ }}$.

(iii). $\angle ADC$

Ans: Since AB||CD

$\angle BAC=\angle ACD$ (Alternate angles)

$\angle ACD={{25}^{\circ }}$  (from figure $\angle BAC={{25}^{\circ }}$)

By using angle sum property in $\Delta ADC$

$\angle ACD+\angle CAD+\angle ADC={{180}^{\circ }}$

$\Rightarrow \angle ADC={{180}^{\circ }}-{{25}^{\circ }}-{{55}^{\circ }}={{100}^{\circ }}$ $\left[\text{From (i) part} \angle CAD={{55}^{\circ }}\right]$

Thus the value of $\angle ADC$ is ${{100}^{\circ }}$.

21. ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that $APB={{60}^{\circ }}$.

Ans: 

Given, Chord CD= radius OD=radius OC

Therefore, $\Delta DOC$ is an equilateral triangle.

Let $\angle A=x$ and $\angle B=y$

∵AO=DO and OC=OB (radii of circle)

∴$\angle A=\angle ODA$ and $\angle B=\angle OCB$(opposite angles of equal sides are equal)

By using angle sum property in $\Delta AOD$ and $\Delta BOC$

 In $\Delta AODx+x+\angle AOD={{180}^{\circ }}\Rightarrow \angle AOD={{180}^{\circ }}-2x$

Similarly, In $\Delta BOC$ $y+y+\angle BOD={{180}^{\circ }}\Rightarrow \angle BOD={{180}^{\circ }}-2y$

AOB is a straight line, 

$\angle AOD+\angle BOC+\angle DOC={{180}^{\circ }}$

$\Rightarrow {{180}^{\circ }}-2x+{{180}^{\circ }}-2y+{{60}^{\circ }}={{180}^{\circ }}$

$\Rightarrow 2x+2y={{420}^{\circ }}-{{180}^{\circ }}={{240}^{\circ }}$

$\Rightarrow x+y={{120}^{\circ }}$

In $\Delta APB$ by using the angle sum property,

$\angle APB+x+y={{180}^{\circ }}$

$\Rightarrow \angle APB={{180}^{\circ }}-\left( x+y \right)$

$\Rightarrow \angle APB={{180}^{\circ }}-{{120}^{\circ }}={{60}^{\circ }}$

Thus the value of $\angle APB$ is ${{60}^{\circ }}$.

22. In the figure, given below, CP bisects angle ACB. Show that DP bisects angle ADB.

Ans: Since CP is an angle bisector of $\angle ACB$.

Hence, $\angle ACP=\angle BCP$-----(1)

Angles at the circumference subtended by the same chord are equal.

 $\angle ACP=\angle ADP$ (Subtended by the chord AP)---------(2)

$\angle BCP=\angle BDP$ (Subtended by the chord PB)---------(3)

By eq. (1), (2) and (3)

$\angle ADP=\angle BDP$

Therefore, DP is a bisector of angle BDA.

23. In the figure, given below, AD=BC, $\angle BAC={{30}^{\circ }}$ and $\angle CBD={{70}^{\circ }}$. Find :

(i). $\angle BCD$

Ans: Angles at the circumference subtended by the same chord are equal.

$\angle CAD$ and $\angle CBD$ are subtended by the same chord CD.

$\angle CAD=\angle CBD={{70}^{\circ }}$

$\angle BAC=\angle BDC={{30}^{\circ }}$(Subtended by the chord BC)

Since, $\angle BAD=\angle BAC+\angle CAD={{30}^{\circ }}+{{70}^{\circ }}={{100}^{\circ }}$

ABCD is a cyclic quadrilateral and in cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$

$\angle BAD+\angle BCD={{180}^{\circ }}$

$\Rightarrow \angle BCD={{180}^{\circ }}-{{100}^{\circ }}={{80}^{\circ }}$

Thus the value of $\angle BCD$ is ${{80}^{\circ }}$.

(ii). $\angle BCA$

Ans: Since AD=BC and ABCD is an isosceles trapezium. Hence AB||CD.

$\angle DCA=\angle BAC={{30}^{\circ }}$(Alternate angles)

Since, $\angle BCA+\angle DCA=\angle BCD$

$\Rightarrow \angle BCA={{80}^{\circ }}-{{30}^{\circ }}={{50}^{\circ }}$  ( From i part $\angle BCD={{80}^{\circ }}$)

Thus the value of $\angle BCA$ is ${{50}^{\circ }}$.

(iii). $\angle ABC$

Ans: In $\Delta ABC$ by using angle sum property,

$\angle ABC+\angle BCA+\angle BAC={{180}^{\circ }}$

$\angle ABC={{180}^{\circ }}-{{50}^{\circ }}-{{30}^{\circ }}={{100}^{\circ }}$

Thus the value of $\angle ABC$ is ${{100}^{\circ }}$.

(iv). $\angle ADB$

Ans: In a circle, Angles at the circumference subtended by the same chord are always equal. $\angle ADB$ and $\angle BCA$ are subtended by the chord AB.

$\angle ADB=\angle BCA={{50}^{\circ }}$ (From ii part $\angle BCA={{50}^{\circ }}$)

Thus the value of $\angle ADB$ is ${{50}^{\circ }}$.

24. In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and $\angle CBD={{32}^{\circ }}$. Find :

(i). $\angle OBD$

Ans: Since, AD||BC ⇒OD||BC

Therefore, $\angle ODB=DBC={{32}^{\circ }}$ (Alternate angles)------(1)

Since, OB=OD (radii of circle)

$\angle OBD=\angle ODB$------------(2)

By equation (1) and (2)

$\Rightarrow \angle OBD={{32}^{\circ }}$

(ii). $\angle AOB$

Ans: In $\Delta BOD$ by using angle sum property,

$\angle OBD+\angle ODB+\angle BOD={{180}^{\circ }}$

$\Rightarrow \angle BOD={{180}^{\circ }}-2\angle OBD={{180}^{\circ }}-{{64}^{\circ }}={{116}^{\circ }}$

AD is a diameter that means AOD is a straight line. Hence $\angle AOB$ and $\angle BOD$ is a linear pair.

$\angle AOB+\angle BOD={{180}^{\circ }}$

$\Rightarrow \angle AOB={{180}^{\circ }}-{{116}^{\circ }}={{64}^{\circ }}$

(iii). $\angle BED$

Ans: OA=OB (radii of circle)

$\angle OAB=\angle OBA$(opposite angles of  equal sides are equal)

In $\Delta AOB$ by using angle sum property, 

$\angle OAB+\angle OBA+\angle AOB={{180}^{\circ }}$

$\Rightarrow 2\angle OAB={{180}^{\circ }}-{{64}^{\circ }}={{116}^{\circ }}$

$\Rightarrow \angle OAB=\dfrac{{{116}^{\circ }}}{2}={{58}^{\circ }}$

$\angle DAB=\angle OAB={{58}^{\circ }}$ (Angle b/w same line segment)

Angles at the circumference subtended by the same chord are equal. Here $\angle BED$ and $\angle DAB$ are subtended by the chord BD.

$\angle BED=\angle DAB={{58}^{\circ }}$

Thus the value of $\angle BED$ is ${{58}^{\circ }}$.

25. In the figure given, O is the centre of the circle. $\angle DAE={{70}^{\circ }}$. Find giving suitable reasons, the measure of 

(i).$\angle BCD$

Ans: $\angle DAB$ and $\angle DAE$ is a linear pair. Therefore, 

$\angle DAB+\angle DAE={{180}^{\circ }}$

$\Rightarrow \angle DAB={{180}^{\circ }}-{{70}^{\circ }}={{110}^{\circ }}$

ABCD is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is ${{180}^{\circ }}$.

$\angle DAB+\angle BCD={{180}^{\circ }}$

$\Rightarrow \angle BCD={{180}^{\circ }}-{{110}^{\circ }}={{70}^{\circ }}$

Thus the value of $\angle BCD$ is ${{70}^{\circ }}$.

(ii). $\angle BOD$

Ans: In a circle, Angle at centre is doubled the angle at circumference subtended by the same chord.

Hence, $\angle BOD=2\angle BCD$

$\Rightarrow \angle BOD=2\times {{70}^{\circ }}={{140}^{\circ }}$

Thus the value of $\angle BOD$ is ${{140}^{\circ }}$.

(iii). $\angle OBD$

Ans: Since, OB=OD (radii of circle)

$\angle OBD=\angle ODB$

In $\Delta BOD$ by using angle sum property,

$\angle OBD+\angle ODB+\angle BOD={{180}^{\circ }}_{{}}$

$\Rightarrow 2\angle OBD={{180}^{\circ }}-{{140}^{\circ }}$

$\Rightarrow \angle OBD=\dfrac{{{40}^{\circ }}}{2}={{20}^{\circ }}$

Thus the value of $\angle OBD$ is ${{20}^{\circ }}$.

ICSE Class 10 Mathematics Chapter 17 Selina Concise Solutions

Preparation Tips for Class 10 Maths

Some of the tips to be followed are as below:

1. Make a study plan analyzing the syllabus and the topics to be covered for each day.

2. Practice the theorems and the formulas with proper conceptual understanding.

3. Revise every day whatever has been studied previously.

4. Know the weak and the strong points in the chapter

5. Work more on the weak points.

6. Follow the steps while solving the problem.

7. Try not to skip any topics.

8. Take the mock test and solve the previous year’s question paper.

9. Practice and try to solve the problems quickly.

10. Improve on time management.

11. Enhance the speed of solving the problems.

12. List the formulas and theorems and revise them every day.

Introduction to the Chapter

This chapter teaches the students how two figures have the same shape but differ in size and yet they are called similar figures. This chapter mainly deals with the similarity of triangles, basics of understanding corresponding sides and corresponding angles of similar triangles, various conditions for similarity of two triangles, the Basic Proportionality theorem, the relation between the areas of two triangles, similarity as a size transformation, and finally the applications to maps and models are the main concepts of the chapter.

ICSE Class 10 Maths Solutions to Chapter 15

Students should learn all the concepts and theorems clearly without any confusion. Each chapter and the topics have to be learned with focus and concentration so that they can be easily remembered. 

It is not just learning the concepts but also, to practice to answer relevant questions that are important. 

Class 10 is very crucial and students should prepare well to face the challenges and also should be able to solve any problems given in the exam. 

Class 10 is not just the completion of secondary school but also, students learn a lot of new concepts. The concepts and the chapters give a strong foundation when they enter classes 11 and 12. It becomes very important that the students focus completely on fundamentals. 

The ICSE Solutions will help the students to understand the concepts in a simplified way. The steps provided in solving the problems were very beneficial learning and remembering the concepts.

Chapter 17 teaches the student about the circle and the basic types and parts of a circle, cyclic properties, and some important theorems and results. Students can get clarity of all these topics, concepts, and problem-solving techniques from Vedantu’s ICSE solution.

Maths is a subject that can be grasped only through practice. Students need to have a comprehensive study structure and follow it systematically. To achieve this, one has to plan out what topics to be covered each day.