




An Overview of Class 11 Physics To Measure The Mass Of A Body On A Metre Scale Using The Principle Of Moments Experiment
State the Principle of Moments - The algebraic sum of moments in the clockwise direction is equal to the algebraic sum of moments in the clockwise direction when several forces are acting on a rigid body, and the body is in equilibrium. In other words, the total algebraic sum of all the forces' moments is zero.
Some daily life examples of the principle of moments are opening up a door, transporting materials in a wheelbarrow, using a screwdriver to remove a screw, using a knife to cut open a tin, a ride on a seesaw.
Table of content
Aim
Theory
Observation
Result
Aim
To measure the mass of a body on a metre scale using the principle of moments.
Apparatus Required
A load of unknown mass
A wooden or metal wedge with a sharp edge
A weight box
A thread that is nearly 30 cm long
A spirit level
A raised platform that is about 20 cm high
A wooden metre scale with uniform thickness can also be used
Theory
The sum of the clockwise moments is equal to the sum of the anticlockwise moments for a body free to spin about a fixed axis in equilibrium. \[\]
\[{M_2}{L_2} = {M_1}{L_1}\]
if M1 is the known mass suspended at a distance L1 on one side of a beam's centre of gravity and M2 is the unknown mass suspended at a distance L2 on the other side, and the beam is in equilibrium.
Procedure
On a table, build a raised platform. To execute this, one can utilize a metal or wooden block. However, the platform needs to be strong such that you can lay a wedge on it with a sharp edge.
Alternatively, the wedge can be fixed to a lab stand at a height of roughly 20 cm above the table top. Set the level of the wedge horizontally using a spirit level.
Make two thread loops that will be used to suspend the weights from the metre scale and the unknown mass (beam). Place the loops 10 cm in from each side of the metre scale's edge.
Place the metre scale on the wedge using the thread loops, then tweak it until it is balanced. In the area above the wedge where the scale is balanced, mark two points on the scale. The equilibrium position can be identified by connecting these two points with a straight line, even if the scale tips over from the wedge for whatever reason. This line runs across the scale's centre of gravity.
Pick the unknown weight in one hand and with the other hand pick another weight from the weight box, which appears equal to the unknown weight while holding in hand.
Suspend the unidentified mass from one of the two thread loops connected to the metre scale. Using the other loop, suspend the known weight (Image A).
Move the loop to change the known weight's position until the metre scale is balanced on the acute wedge. Make sure the line drawn in Step 3 is exactly above the wedge in the balanced position and that the thread of the two loops crossing the scale is parallel to this line.
The distance between the loops' current locations and the line drawn in Step 3 should be measured. Keep a record of your findings.
Repeat the activity at least twice using a slightly lighter and heavier weight. Take note of each case's unknown mass and weight offsets from the step 3 line.
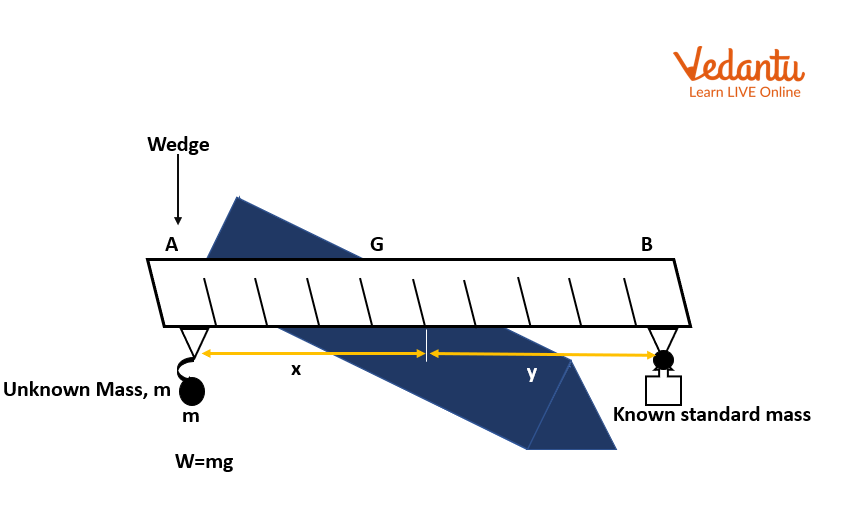
Experimental Diagram
Observations
Position of the centre of gravity=________cm.
Calculations
The moment of the force on one side of the wedge will be equal to the moment of the force on the other side in the balanced position of the meter scale.
Moment of the force due to known weight = \[\begin{array}{l}({M_1}.{L_1})g\\\end{array}\]
Moment of the force due to unknown weight =\[{M_2}.{L_2}(g)\]
In balanced position,
\[\begin{array}{l}{M_1}.{L_1} = {M_2}.{L_2}\\{M_2} = \dfrac{{{M_1}.{L_1}}}{{{L_2}}}\end{array}\]
Average mass of unknown load = ______g
Result
Mass of the given body = _____g
Precautions
The wedge must be sharp and always perpendicular to the scale's length.
The length of the scale should be perpendicular to the thread loops.
Thin, light, and strong thread should be used for the loops.
Reduce air currents as much as possible.
Lab Manual Questions
1. What is the term for the point on the scale when it is horizontally balanced on the wedge?
Ans: Pivot
2. How is the accuracy of mass measurement limited by the metre scale's least count?
Ans: Therefore, 0.1 cm or 1 mm is the least count on the metre scale.
3. Explain how the principle of moments are used in physical balances.
Ans: According to the Principle of Moments, the total clockwise and anticlockwise moments about a given point are equal when a body is balanced. That is why the principle of moments is used in physical balances.
4. What issues might air currents bring about with this activity?
Ans: Air currents will make an issue while balancing the meter scale on the wedge.
Practical Based Questions
1. How does the moment principle relate to the beam's balance?
Ans: If all of the moments acting on an item during static equilibrium are equal to zero, the object will not rotate. The sum of the clockwise moments should equal the sum of the anticlockwise moments if the net sum of the moments of the forces is zero.
2. Describe the moment of force.
Ans: The product of the force's magnitude and the line of action's perpendicular distance produces the moment of force. Therefore, force x perpendicular distance of force from point O equals moment of force about a given axis passing through point O.
3. How do we write a dimensional formula for the moment of force?
Ans: The moment of force is the tendency to cause the rotation of an object about its axis.
Mathematically, the definition of a moment of force is
\[force \times dis\tan ce\]
The Force’s dimensional formula is \[{M^1}{L^1}{T^{ - 2}}\] .
The distance’s dimensional equation is \[{M^0}{L^1}{T^0}\]
4. What is the distance between the point of application of the force and the point if the moment of force of 20 N around a point is specified as 4 Nm?
Ans: We know that,
\[\begin{array}{l}{\rm{moment of force = force}} \times {\rm{distance}}\\{\rm{4 Nm = 20 N}} \times {\rm{r}}\\{\rm{r = 0}}{\rm{.2 m}}\end{array}\]
5. What does a force moment look like in everyday life?
Ans: The best illustration of a moment of force in our daily life is a see-saw that we swing on in a park. The swing remains in a balanced position when weight is applied to both sides of a see-saw to balance the moment, but the swing does not remain in a balanced position if greater weight is applied to one side. This is referred to as an imbalanced moment, as a result. The idea of the moment of force is evident in many more instances throughout our daily lives.
6. Calculate the force's moment if a 30 N force acts at a 0.20 m perpendicular distance from the turning point.
Ans: we know that,
\[\begin{array}{l}Moment = f \times d\\moment = 30N \times 0.20m\\moment = 6Nm\end{array}\]
7. List out 4 applications of the principle of moments.
Ans: Four applications of principle of moments are:
Opening up a door.
Transporting materials in a wheelbarrow.
Using screwdriver to remove a screw.
A ride on a seesaw.
8. From the diagram below, determine the resultant moment:
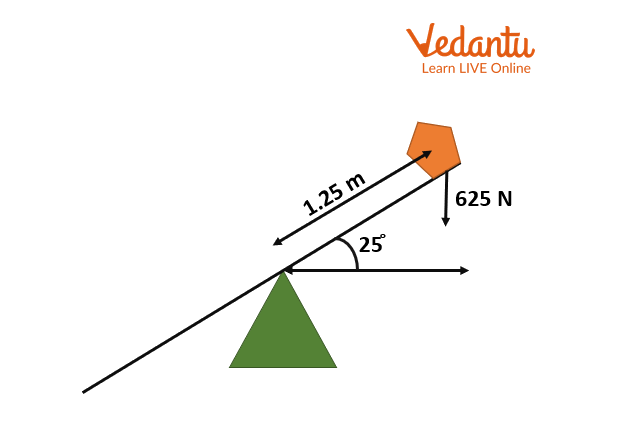
Ans:
\[\begin{array}{l}{\rm{Perpendicular distance = 1}}{\rm{.25cos(25) = 1}}{\rm{.13m}}\\{\rm{Moment = 625}} \times {\rm{1}}{\rm{.13 = 708 Nm}}\end{array}\]
9. Explain why it would be preferable for a forklift truck to transport its cargo near to the ground rather than higher up in the air using your understanding of the centre of mass.
Ans: The centre of mass of the load and the vehicle move closer to the earth as the mass of the load is lowered toward the ground. This increases the load's and forklift truck's stability.
Viva Questions
1. What exactly is a moment?
A force's turning effect.
A point's mass of an object.
The distance between a mass and a pivot.
When a system is balanced.
Ans: A) A force’s turning effect
2. What is the formula for size of the moment?
\[M = f \times d\]
\[F = M \times d\]
\[M = \dfrac{F}{d}\]
\[d = M \times f\]
Ans: A) \[M = f \times d\]
3. What does the symbol d in the previous equation mean?
The parallel distance between the action line and the pivot.
The perpendicular distance between the pivot and the action line.
Distance between the two planes.
Distance of the plane.
Ans: B) The perpendicular distance between the pivot and the action line.
4. What must the total clockwise moment be about any pivot if the item is not rotating, as opposed to the total anti-clockwise moment?
The magnitude of the clockwise moment is double than that of the anticlockwise moment.
The amount of the clockwise moment is three times that of the anti-clockwise moment.
Anti-clockwise moment has a half-size compared to clockwise moment.
The anti-clockwise moment and the clockwise moment have exactly the same magnitude.
Ans: D) The anti-clockwise moment and the clockwise moment have exactly the same magnitude.
5. What would happen to the moment if the point of force's application was shifted further from the pivot?
Due to the greater distance, the moment would be bigger.
The force hasn't altered, thus the moment would stay the same.
Since it is further away, the moment would be less and have less of an impact on the pivot.
In order to adequately respond to this question, further details are required.
Ans: A) Due to the greater distance, the moment would be bigger.
6. Which of the following illustrates the use of the moments principle?
A rock falling
Lifting up a book
A USB stick
A crowbar being used to lift a drain cover
Ans: D) A crowbar being used to lift a drain cover
7. Which option is correct for state of equilibrium in principle of moment
Resultant moment should be zero
The tension must be equal on both sides
Both objects' weights should balance out on the beam.
The two objects should be the same distance apart in the beam balance.
Ans: A) Resultant moment should be zero
8. According to the principle of moments, the motion of the centre of mass depends upon
Total internal forces
Total external forces
Both A and B
None of the above
Ans: B) Total external forces
9. On a line, where does the centre of mass of a two particle lies,
At any angle on this line
Joining the particles
Perpendicular to the line joining the particles
None of the above
Ans: B) Joining the particles
10. Where does the centre of mass of a system of particles does not depend upon
Mass of the particle
Symmetry of the body
Position of the particle
None of the above
Ans: D) none of the above
Conclusion
From this experiment, we can see that when two pans are filled with weights that are slightly different from one another, a beam balance will come to rest at an angle to the horizontal. The beam is supported by a pivot at a single fixed point. The net torque produced by the two weights around this single fixed point is not zero at the equilibrium position. The system stops rotating around the fixed point because the moment is balanced.
FAQs on Class 11 Physics To Measure The Mass Of A Body On A Metre Scale Using The Principle Of Moments Experiment
1. For a Class 11 Physics practical exam, what is the principle of moments and how is it applied to determine the mass of a body?
The principle of moments states that for a body to be in rotational equilibrium, the sum of all clockwise moments about a pivot point must be equal to the sum of all anticlockwise moments about the same point. In this experiment, a metre scale is balanced on a pivot. An unknown mass (m) and a known mass (M) are suspended on opposite sides. By adjusting their distances (d and D respectively) from the pivot until the scale is horizontal, we achieve equilibrium. The mass is then calculated using the formula: Anticlockwise Moment = Clockwise Moment, which translates to m × d = M × D.
2. Describe the step-by-step procedure to find the mass of an unknown object using a metre scale, as expected for a 3-mark question.
To determine the mass of an unknown object using the principle of moments, follow these steps:
Step 1: Place the metre scale on the pivot (fulcrum) and adjust it until it balances horizontally. Note this point as the centre of gravity (C), which is usually at the 50 cm mark for a uniform scale.
Step 2: Suspend a known standard weight (M) from a hanger on one side of the fulcrum.
Step 3: Suspend the unknown mass (m) on the other side of the fulcrum.
Step 4: Adjust the position of either the known or unknown mass until the metre scale becomes perfectly horizontal again.
Step 5: Measure the perpendicular distance of the known mass (D) and the unknown mass (d) from the fulcrum.
Step 6: Apply the principle of moments (m × d = M × D) to calculate the unknown mass 'm'. Repeat the process for different positions to ensure accuracy.
3. A uniform metre rule balances at the 50 cm mark. If a known mass of 100 g is hung at the 35 cm mark, where must an unknown mass of 50 g be hung to balance the rule? This is a frequently asked problem type.
To solve this, we apply the principle of moments. The pivot is at the 50 cm mark.
The known mass (M) = 100 g is at the 35 cm mark, creating an anticlockwise moment.
Distance of known mass from pivot (D) = 50 cm - 35 cm = 15 cm.
The unknown mass (m) = 50 g will create a clockwise moment.
Let its distance from the pivot be 'd'.
According to the principle of moments: Clockwise Moment = Anticlockwise Moment.
m × d = M × D
50 × d = 100 × 15
50d = 1500
d = 30 cm
Therefore, the 50 g mass must be hung 30 cm from the pivot on the opposite side, which is at the 50 cm + 30 cm = 80 cm mark.
4. What are the most common sources of error in this experiment, and how can they be minimised for more accurate results?
This is a crucial question for viva voce and assesses deeper understanding. The primary sources of error are:
Non-uniform Metre Scale: The centre of gravity may not be at the 50 cm mark. To minimise, find the actual centre of gravity by balancing the scale without any weights first and use that as the pivot point for all calculations.
Parallax Error: Incorrectly reading the positions on the scale due to the eye's viewing angle. To minimise, ensure your eye is directly above the marking being read.
Thick Suspension Threads: The weight of the threads or hangers can affect the moments. To minimise, use threads that are as thin and light as possible but strong enough to hold the weights.
Air Currents: Disturbance from a fan or breeze can prevent the scale from balancing correctly. To minimise, perform the experiment in a closed room with minimal air movement.
5. Why is it important to use thin, strong threads for suspending the weights and to ensure the metre scale is perfectly horizontal?
This question tests the fundamental assumptions of the experiment.
Thin, Strong Threads: Threads must be thin and light so their own mass is negligible and does not contribute a significant moment to the system, which would be an un-accounted error. They must be strong to support the weights without breaking.
Perfectly Horizontal Scale: The principle of moments relies on the lever arms (distances) being measured perpendicular to the line of action of the forces (weights). When the scale is horizontal, the weights act vertically downwards, and the distances along the scale are the correct perpendicular lever arms. If the scale is tilted, the lever arms change, making the simple formula m × d = M × D inaccurate.
6. How would you proceed if the provided metre scale is not uniform, i.e., its centre of gravity is not at 50 cm? Is it still possible to find the unknown mass?
Yes, it is still possible to find the unknown mass, but the procedure requires an additional step. This is a higher-order thinking (HOTS) variation of the experiment.
First, find the true centre of gravity (C.G.) of the non-uniform scale by balancing it on the pivot without any weights. Let's say it balances at 48 cm.
The entire weight of the scale (W) can be considered to act at this C.G. (48 cm mark).
Now, when you suspend the known and unknown masses, the weight of the scale itself will create a moment if the fulcrum is not placed at the C.G. To simplify, it's best to use the C.G. (48 cm) as the pivot point. In this case, the weight of the scale produces no moment, and the experiment proceeds as usual with the formula m × d = M × D, where 'd' and 'D' are distances from the 48 cm mark.
7. What observations should be recorded in a tabular format for the metre scale experiment to ensure systematic data collection for the CBSE Class 11 Physics practical file (2025-26)?
For systematic data collection and calculation, the observation table is a key component. A well-structured table for this experiment should include the following columns:
Serial No.
Position of Fulcrum / C.G. (C) in cm
Known Mass (M) in g
Position of Known Mass (A) in cm
Position of Unknown Mass (B) in cm
Distance of Known Mass from Fulcrum (D = |A - C|) in cm
Distance of Unknown Mass from Fulcrum (d = |B - C|) in cm
Calculated Unknown Mass (m = M × D/d) in g
Recording multiple readings and then taking the mean of the calculated mass 'm' is an important practice to get a more accurate final result.
























