NCERT Exemplar for Class 6 Maths Solutions Chapter 6 Mensuration

Solved Examples

Example 1: Choose the correct answer from the given four options:

In Fig. 6.1, a square of side 1 cm is joined to a square of side 3 cm. The perimeter of the new figure is

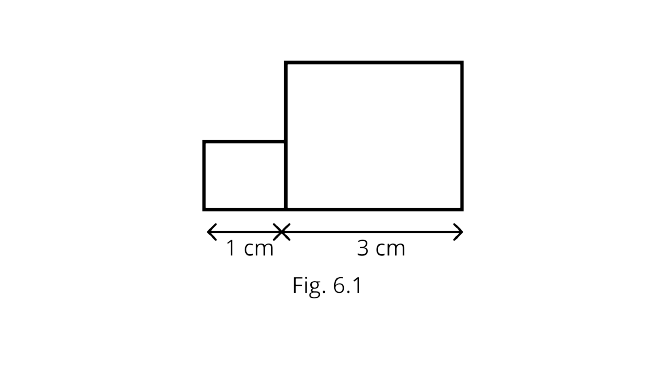
(A) 13cm

(B) 14cm

(C) 15cm

(D) 16cm

Ans: Correct option - B

Because we know that perimeter=sum of all sides

$=3+3+3+1+1+1+2=14$cm.

Example 2: Which of the following statements are true or false?

(a) Geeta wants to raise a boundary wall around her house. For this, she must find the area of the land of her house.

Ans: False 

Boundary wall is around her house, so she must find the perimeter of the land.

(b) A person preparing a track to conduct sports must find the perimeter of the sports ground.

Ans: True 

Because the track is prepared along the boundary of the sports ground.

Example 3: Fill in the blanks to make the statements true:

(a) Perimeter of a triangle with sides $4.5$cm, $6.02$cm and $5.38$cm is………

Ans: Perimeter of a triangle with sides $4.5$cm, $6.02$cm and $5.38$cm is $15.9$cm.

Because we know that perimeter=sum of all sides

$=4.5+6.02+5.38=15.9$cm.

(b) Area of a square of side 5cm is………

Ans: Area of a square of side 5cm is 25sqcm.

Because we know that area of a square=$\text{side}^{2}$=${5}^{2}=25$sqcm.

Example 4: Bhavna runs 10 times around a square field of side 80m. Her sister Sushmita runs 8 times around a rectangular field with length 150m and breadth 60m.

Who covers more distance? By how much? 

Ans: For Bhavna

Distance = Perimeter of the square field = $4 \times$ side of square field

$=4 \times 80 = 320$m

Distance covered in 10 rounds = $320 \times 10= 3200$m

For Sushmita

Distance = Perimeter of the rectangular field = $2 \times$(length + breadth)

$= 2 \times(150 + 60) = 2 \times 210 = 420$m

Distance covered in 8 rounds = $420 \times 8 = 3360$m

So, Sushmita has covered more distance than Bhavna.

Difference = $3360-3200=160$m

Example 5: The length of a rectangular field is thrice its breadth. If the perimeter of this field is 800m, what is the length of the field?

Ans: Given,perimeter of this field is= 800m

length of the rectangular field $=3 \times$ breadth

We know that perimeter of a rectangle $=2 \times$(length + breadth)

perimeter of field $=2 \times (3 \times \text{breadth + breadth})$

$= 2 \times (4 \times \text{breadth})= 8 \times \text{breadth}= 800$

breadth= $\dfrac{{800}}{{8}}$

breadth=$100$m 

And length = $3\times 100$m $=300$m

Example 6:Cost of fencing around a square field is Rs. 12000. If the cost of fencing per metre is Rs. 30, find the area of the square field.

Ans: Given,cost of fencing per metre =Rs 30

Total cost of fencing=Rs 12000

than the length of fencing (perimeter) = $\dfrac{\text{Total cost}}{\text{cost per metre}}$

=$\dfrac{12000}{30}$

=$400$m

Now, length of fencing = Perimeter of the square field

$400=4 \times $side of the field 

$\dfrac{400}{4}$= side of the field

$100$m=side of the field

And, area of the field= $1000 \times 100=10000$sq m.

Example 7: Sabina wants to cover the floor of her room whose length is 4 m and breadth is 3m by square tiles. If each square tile is of side 20cm, then find the number of tiles required to cover the floor of her room.

Ans: Given, length of the room= $4$m = $400$cm 

Breadth of the room=$3$m= $300$cm

Than area of the floor of the room =Length $\times$ Breadth

$= 400 \times 300$sqcm $= 120000$sqcm

Side of the square tile = 20cm

Than area of the square tile = Side $\times$ Side $= 20 \times 20 = 400$sqcm

So, number of tiles required $=\dfrac{120000}{400}$

$=300$

Example 8: By splitting the figure into rectangles, find its area. (see Fig. 6.2)

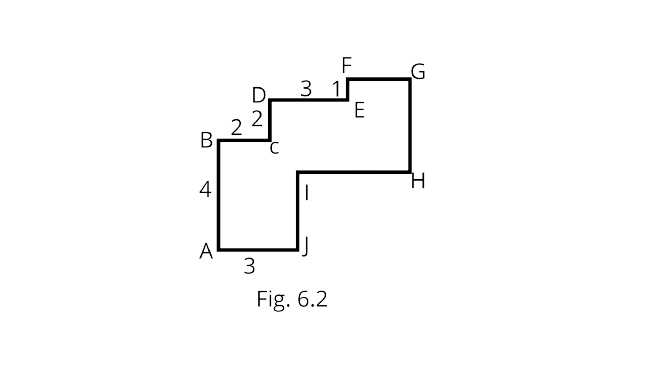
Ans: Firstly we split the figure into four rectangles.

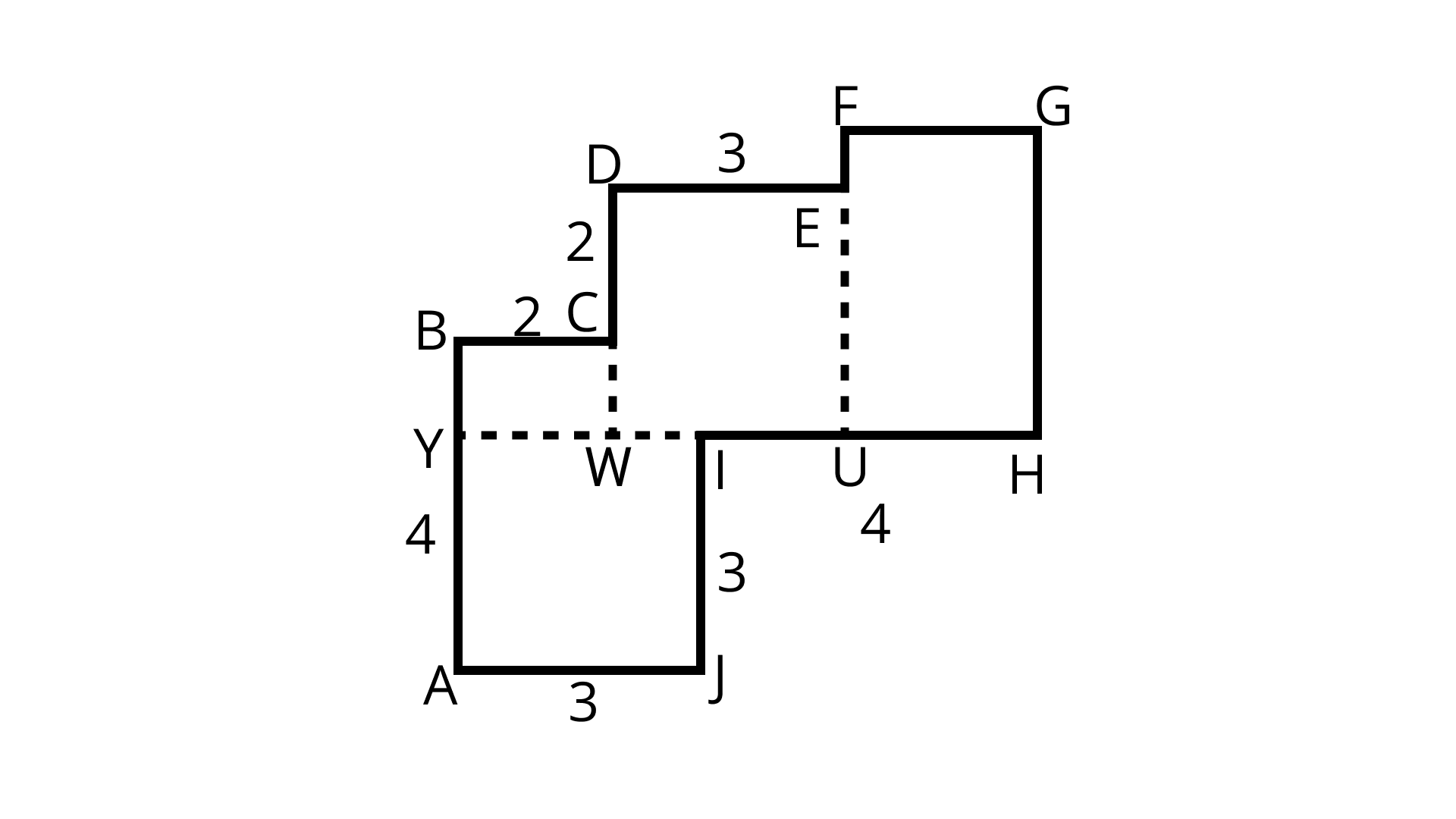
Area of the $\text{AJIY+ YWCB + DWUE+ FUHG}$….(i)

Area $\text{AJIY} = 3 \times 3=9$

$BY=4-3=1$

Area $\text{YWCB}= 1 \times 2=2$

$\text{DW= DC+CW= 2+1=3}$

than, area  $\text{DWUE}= 3 \times 3=9$

Similarly,$UH=4-2=2$

$GH = FU$ and $FU=EU+ FE =DW+FE=3+1=4 $

So, area of $\text{FUHG}=2 \times 4=8$ 

Put all values in equation (i)

The area of the figure $= 9+2 +9+8 =28$sq units.

Exercise

In questions 1 to 6, out of the four options only one is correct. Write the correct answer.

1. The following figures are formed by joining six-unit squares. Which figure has the smallest perimeter in Fig. 6.4

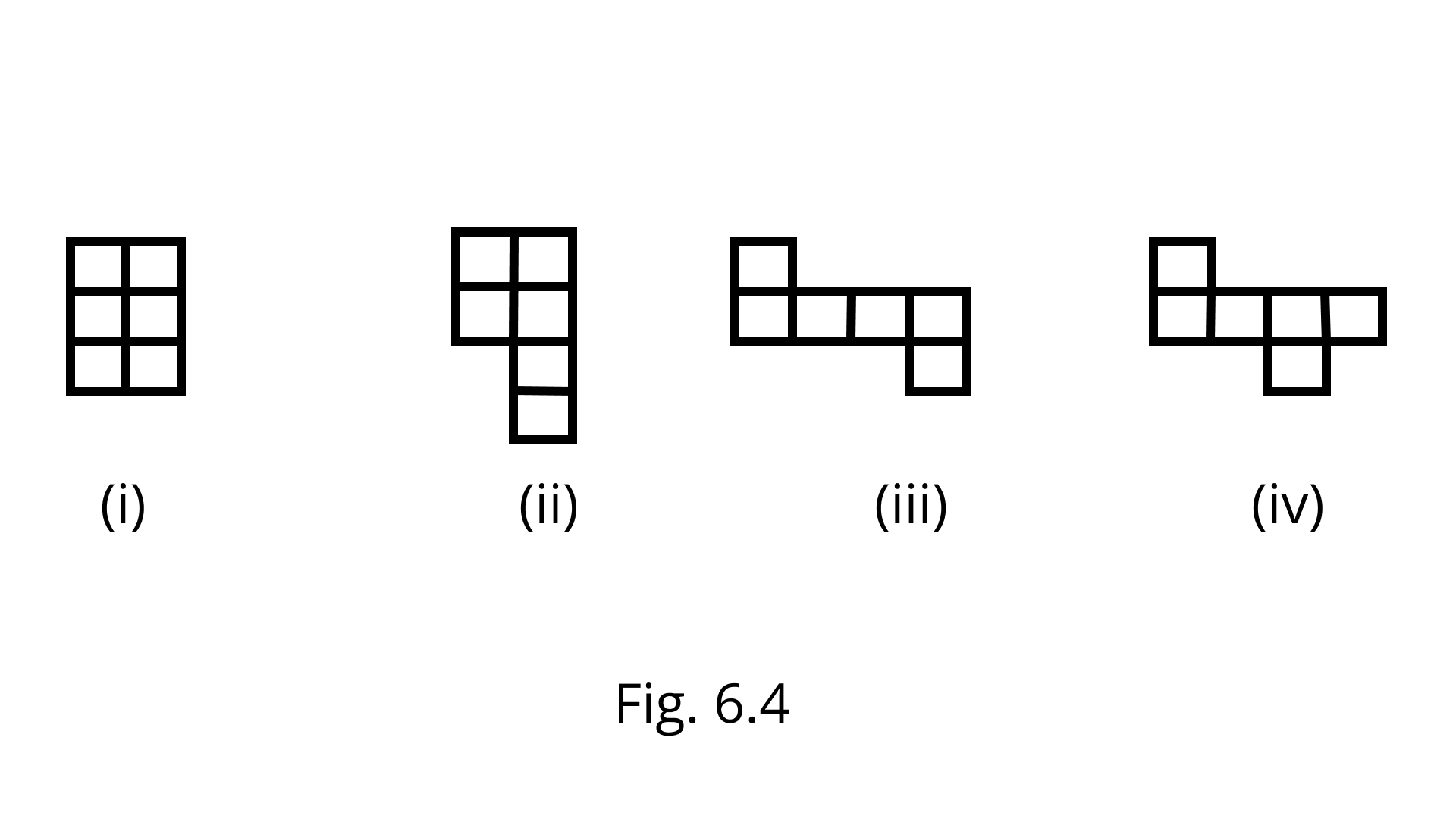
(A) (ii)

(B) (iii)

(C) (iv)

(D) (i)

Ans: Correct option - D 

Perimeter=sum of all sides

For the option (i) = 10 Units:

For the option (ii) = 12 Units

For the option (iii) = 14 Units

For the option (vi) = 14 Units

So, figure (i) has the smallest perimeter.

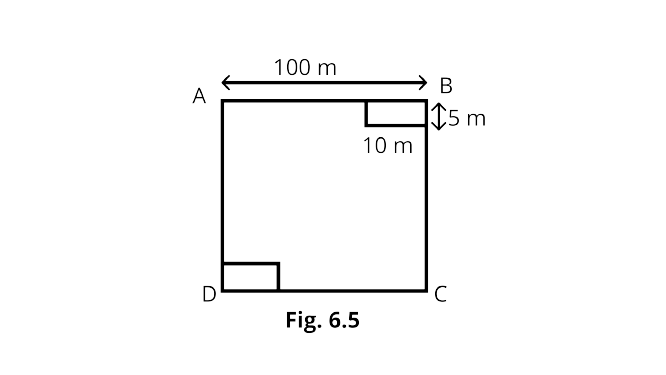
2. A square-shaped park ABCD of side 100m has two equal rectangular flower beds each of size 10m $\times$ 5m. Fig.6.5 Length of the boundary of the remaining park is

(A) 360m

(B) 400m

(C) 340m

(D) 460m

Ans: Correct option - B 

Given ,length =10m

Breadth = 5 m

Than remaining park’s length=90m

Breadth =95m

So, perimeter of remaining park $=90+5+10+95+90+5+10+95=400$m

3. The side of a square is 10cm. How many times will the new perimeter become if the side of the square is doubled?

(A) 2 times

(B) 4 times

(C) 6 times

(D) 8 times

Ans: Correct option - A

Given,side of square = 10 cm

Than perimeter of square= $4 \times$ Sides $=4\times10cm=40cm$

If the side of the square is doubled.

New side of square $=2\times10 cm = 20cm$

Perimeter of new square $=4\times \text{Sides}=4\times20cm=80cm$

So,the new perimeter has doubled from the old perimeter.

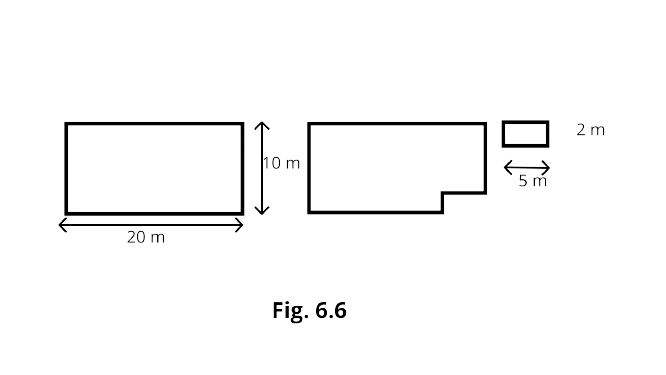
4. The length and breadth of a rectangular sheet of paper are 20 cm and 10 cm, respectively. A rectangular piece is cut from the sheet as shown in Fig.6.6 . Which of the following statements is correct for the remaining sheet?

(A) Perimeter remains the same but area changes.

(B) The area remains the same but the perimeter changes.

(C) Both area and perimeter are changing.

(D) Both area and perimeter remain the same.

Ans: Correct option - A 

Perimeter remains the same as the given figure but the area changes after cutting the piece.

Old perimeter $=2(L+B)=2(20+10)=60m$

New perimeter $=10+20+8+5+2+15=60m$

Old Area $=L \times B =20 \times 10=200{m}^{2}$

New Area $=(20 \times 10)-(5 \times 2)=190{m}^{2}$

5. Two regular Hexagons of perimeter 30cm each are joined as shown in Fig. 6.7. The perimeter of the new figure is

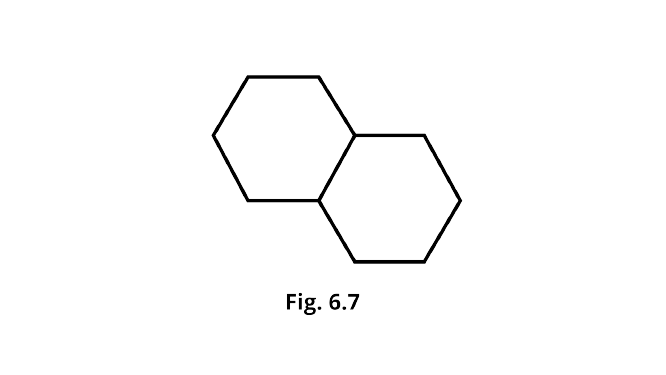
(A) 65cm

(B) 60cm

(C) 55cm

(D) 50cm

Ans: Correct option - D 

Given,Perimeter of hexagon=30cm

Perimeter of hexagon $= 6 \times \text{side}$

$30= 6 \times \text{side}$

$\dfrac{30}{6}$=sides

5cm=side.

So,perimeter of given Figure=$10 \times \text{side}$

$=10\times 5cm=50cm$            $\text{[total number of sides of the new figure is 10]}$

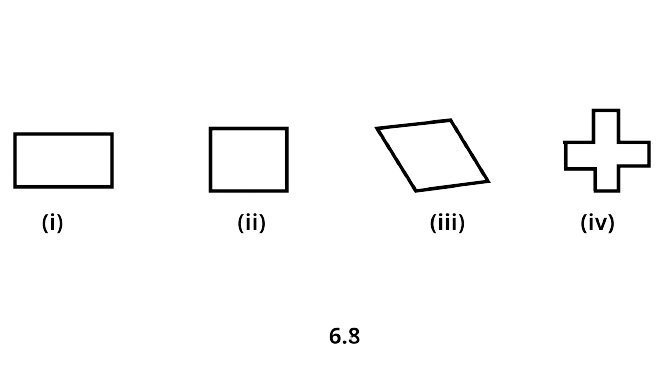
6. In Fig. 6.8 which of the following is a regular polygon? All have equal side except (i)

(A) (i)

(B) (ii)

(C) (iii)

(D) (iv)

Ans: Correct option - B 

Because for a regular polygon, all sides and angles must be equal. Only (ii) is satisfying this condition.

7. Match the shapes (each side's measures 2cm) in column I with the corresponding perimeters in column II:

Column I	Column II
(A) (B) (C ) (D)	(i) 16 cm     (ii) 20 cm (iii) 24 cm (iv) 28 cm (v) 32 cm

Ans: Perimeter of Given figure = sum of all sides

Given ,each side= 2cm

(A) No. of sides=14

Perimeter =14$\times $ length of sides

$=14\times2cm = 28cm$

(B) No. of sides=8

Perimeter =$8\times$ length of sides

$=8\times2cm=16cm$

(C) No. of sides=10

Perimeter =$10\times $ length of side

$=10\times2cm = 20cm$

(D) No. of sides=12

Perimeter$=12\times$ length of sides

$=12\times2cm= 24cm$

Column I	Column II
(A)	(iv) 28 cm
(B)	(i) 16 cm
(C )	(ii) 20 cm
(D)	(iii) 24 cm

8. Match the following.

Shapes	Perimeter
(A)	(i) 10
(B)	(ii) 18
(C )	(iii) 20
(D)	(iv) 25

Ans: Perimeter of Given figure = sum of all sides

(A) We know it's a rectangle.

Perimeter of rectangle$=2\times (l+b)$

$=2\times(6+4)= 2\times 10 = 20 unit$

(B)We know it's a square

Perimeter of square $= 4\times $ length of sides

$=4\times 5$unit $= 20$ unit

(C) We know it's a equilateral triangle 

Perimeter of equilateral triangle $=3\times$ length of side

$=3\times 6$unit $=18 $unit

(D)We know it's a  Isosceles triangle

Perimeter Isosceles triangle=sum of all sides

$=4+4+2= 10$ unit

9. Perimeter of the shaded portion in Fig. 6.9 is

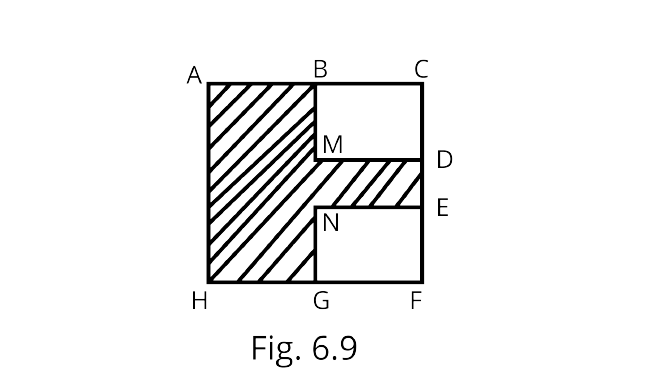
AB+_+_+_+_+_+_+HA

Ans: We know Perimeter = sum of all sides

The sides of given figure AB, BM, MD, DE, EN, NG, GH and HA

So,the perimeter of the given figure = AB + BM + MD + DE + EN + NG + GH + HA.

In questions 9 to 13, fill in the blanks to make the statements true.

10. The amount of region enclosed by a plane closed figure is called its……….

Ans: The amount of region enclosed by a plane closed figure is called its Area.

11. Area of a rectangle with length 5cm and breadth 3cm is……..

Ans: Area of rectangle $= L \times B$

$=5cm\times 3cm=15{cm}^{2}$

12. A rectangle and a square have the same perimeter.

(a) The area of the rectangle is……

Ans:  Area of rectangle$ = L\times B$

$=6 \times 2 = 12{unit}^{2}$

(b) The area of the square is……

Ans: Given,a rectangle and a square have the same perimeter.

So, $2\times(L + B)=4 \times $ sides

Side =$\dfrac{2(L+B)}{4}$

Side =$\dfrac{2(6+2)}{4}$

Side =$\dfrac{2 \times 8}{4}$

Side =$\dfrac{16}{4}$

Side =4unit

Area of Square = $(sides)^{2}$

=$(4unit)^{2}$ = 16$unit^{2}$

13. (a)1m=.......... cm.

Ans: 1m = 100 cm.

(b) 1sqcm=………cm $\times$ 1cm.

Ans: 1sqcm=1cm$\times$ 1cm.

(c) 1sqm = 1m $\times$….....m=100cm $\times$………..cm.

Ans: 1 sqm =1m $\times$ 1m = 100 cm $\times$ 100 cm.

(d) 1sqm=..........sq cm.

Ans: 1 sqm= 10000 sq cm.

In questions 14 to 20, state which of the statements are true and which are false.

14. If the length of a rectangle is halved and breadth is doubled then the area of the rectangle obtained remains the same.

Ans: True

Let. $L$ and $B$ are the length and breadth of the old rectangle and $L ^{\prime}$ and B' length and breadth of the new rectangle.

Than,according to the question

$L ^{\prime}=\dfrac{1}{2} L$ and $B ^{\prime}=2 B$

So,the area of given rectangle=$L \times B$

And area of new rectangle $= L^{\prime} \times B ^{\prime}=\dfrac{1}{2} L \times 2 B = L \times B$

Hence, the area of the rectangle obtained remains the same.

15. Area of a square is doubled if the side of the square is doubled.

Ans: False

Let, the side of square is $A$

Than area of square $= A ^{2}$

According to the question,if the side of the square is doubled

The side of new square is $=2 A$

And area of new square $=(2 A )^{2}=4 A ^{2}$

16. Perimeter of a regular octagon of side $6 cm$ is $36 cm$. 

Ans: False

Sides = 8

So, perimeter Of hexagon $=8\times sides$

$8 \times 6=48 cm$

17. A farmer who wants to fence his field must find the perimeter of the field.

Ans: True

Because ,perimeter is the measure of the boundary.

18. An engineer who plans to build a compound wall on all sides of a house must find the area of the compound.

Ans: False

He must find the perimeters of the compound, not the area.

19. To find the cost of painting a wall we need to find the perimeter of the wall.

Ans: False

Because,to find the cost of painting a wall we need to find the Area of the wall,not perimeter.

20. To find the cost of a frame of a picture, we need to find the perimeter of the picture.

Ans: True

Because to find the cost of a frame of a picture, we need to find the perimeter of the picture.

21. Four regular hexagons are drawn so as to form the design as shown in Fig. 6.11 If the perimeter of the design is $28 cm$, find the length of each side of the hexagon.

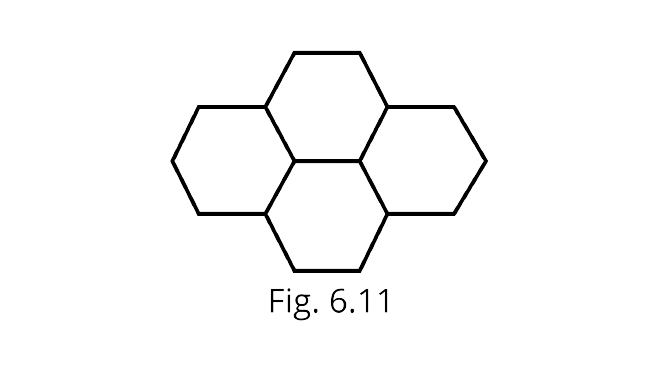
Ans: Given, the perimeter of figure $=28cm$

No. of Sides=14

$14 \times \text { side }=28 cm$ 

$\text { side }=\dfrac{28}{14} cm =2 cm$

So, the length of each side of the hexagon is 2cm.

22. The perimeter of an isosceles triangle is $50 cm$. If one of the two equal sides is $18 cm$, find the third side.

Ans:Given,perimeter=50cm

We know Perimeter = sum of all sides

$50=a+b+c$

$50=18+18+c$

$50=36+c$

$50-36=c$

$14cm=c$

Third side = 14cm.

23. The length of a rectangle is three times its breadth. The perimeter of the rectangle is $40 cm$. Find its length and breadth.

Ans: Given,perimeter of the rectangle = $40 cm$

Let $L$ and $B$ are the length and breadth of rectangle

According to the question $L =3 B$

Perimeter of the rectangle $=2 \times( L + B )$

$40 =2 \times(3 B + B )$

$40=2 \times 4 B =8 B$

$\dfrac{40}{8}$=B

$5 cm=B$

And length=3$\times 5=15$

24. There is a rectangular lawn $10 m$ long and $4 m$ wide in front of Meena's house (Fig. 6.12). It is fenced along the two smaller sides and one longer side leaving a gap of $1 m$ for the entrance. Find the length of fencing.

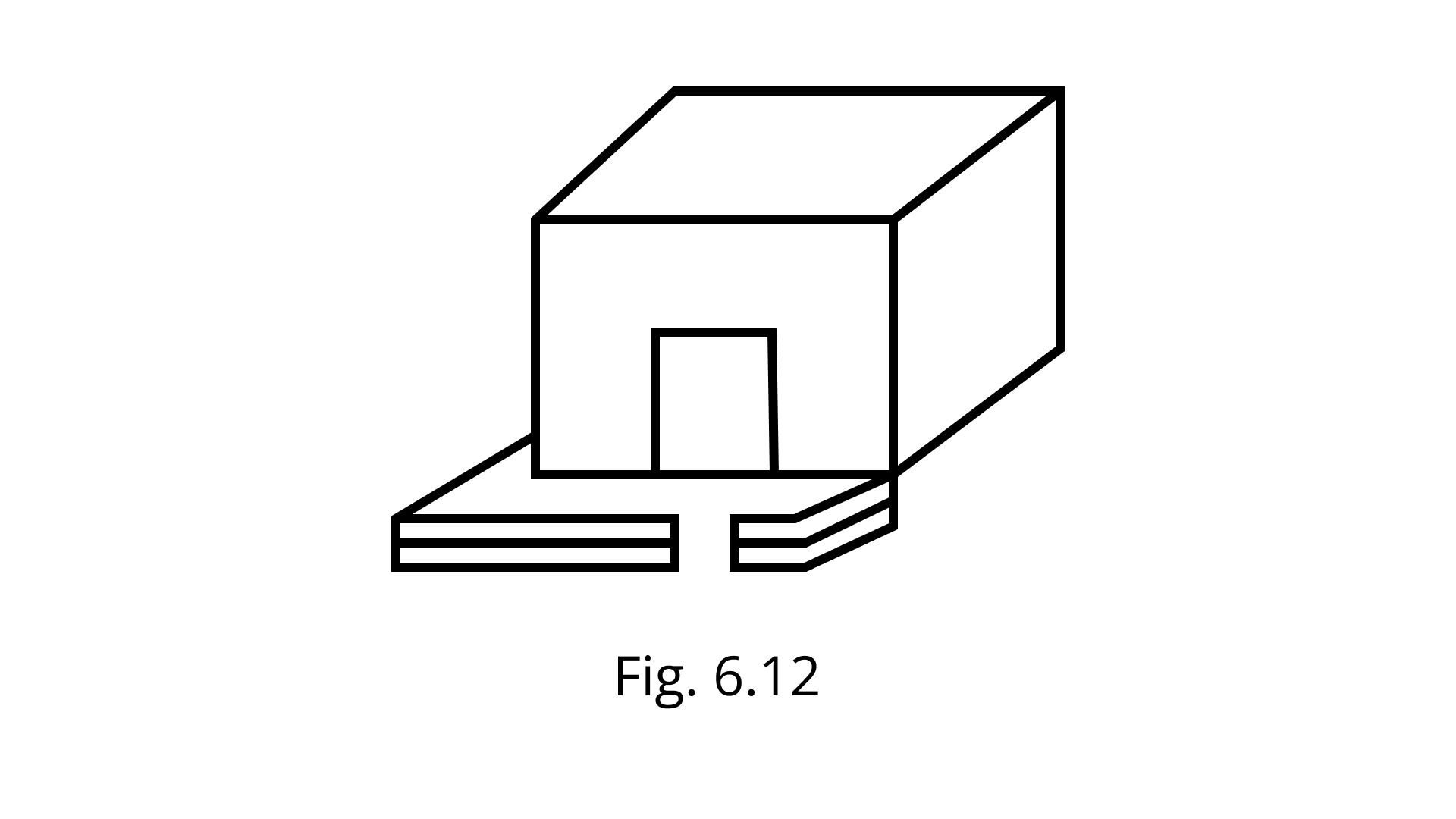
Ans:In rectangular lawn length=10m

And breath = $4 m$

Than the length of fenced along the two smaller sides of lawn

$4 m +4 m =8 m$

Total fencing = $8m+10m-1m=17m$

25. The region given in Fig. 6.13 is measured by taking a rectangle ($\square $) as a unit. What is the area of the region?

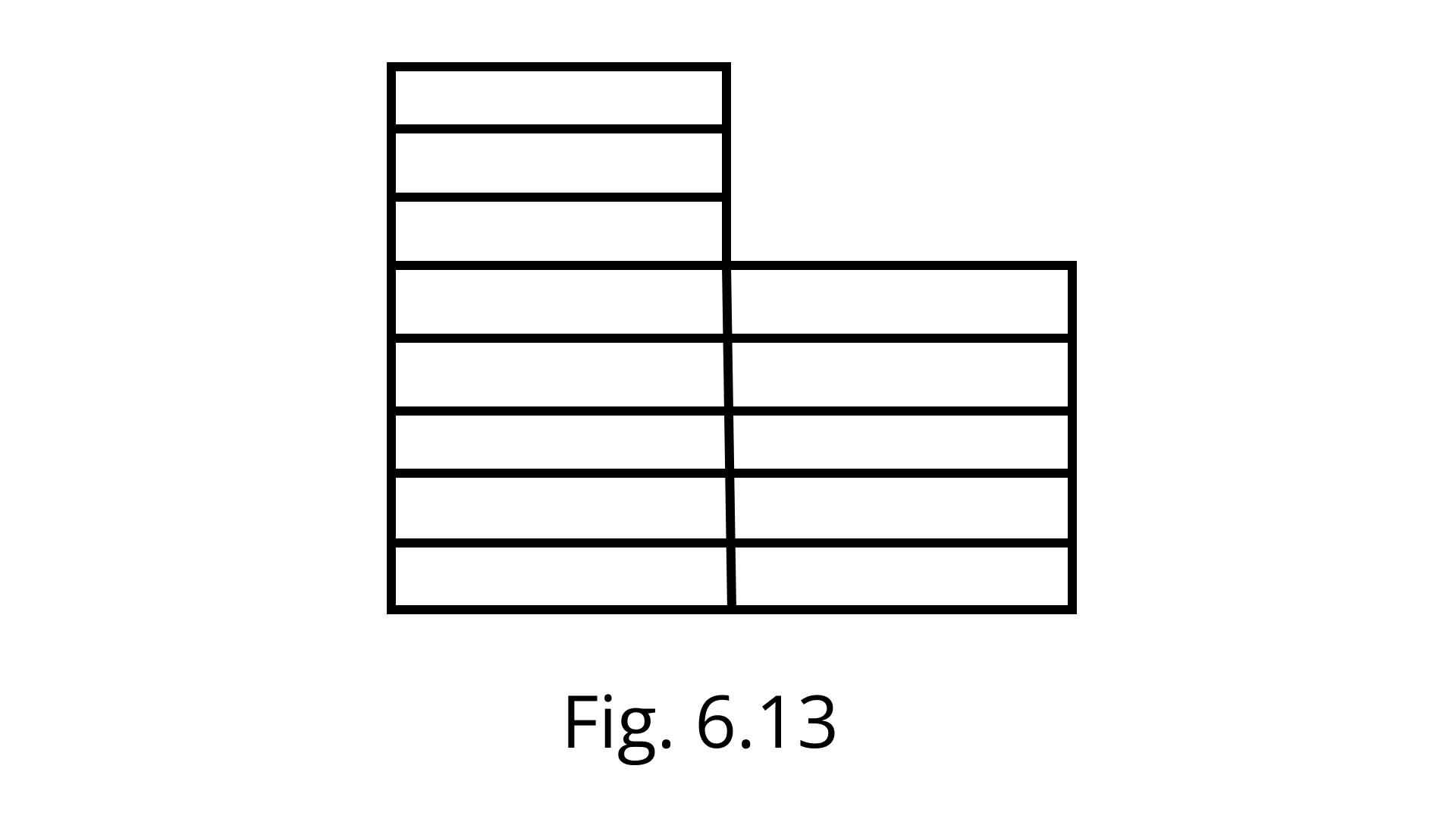
Ans: There are 13 rectangular shapes in the figure

So, area of the region $=13$ sq units

26. Tahir measured the distance around a square field as 200 rods (lathi). Later he found that the length of this rod was $140 cm$. Find the side of this field in meters.

Ans: Given,the length of the road $=140 cm$

Perimeter = the distance around a square field

$4 \times$ side $=$ length of 200 rods

$4 \times \text { side }=200 \times 140 cm$

$\text { Side }=\dfrac{200 \times 140}{4}$

$=\dfrac{28000}{4} cm =7000 cm$

So,length of the side $=70 m$

27. The length of a rectangular field is twice its breadth. Jamal jogged around it four times and covered a distance of $6 km$. What is the length of the field?

Ans: Let. $L$ and $B$ are the length and breadth of the rectangle.

Given, $L =2 B$

Perimeters $=2 \times( L + B )$

According to the question 

$4 \times[2 \times( L + B )]=6 km$

$4 \times[2( L + B )]=6 km$

$8 \times(2 B + B )=6 km$

$8 \times 3 B =6 km$

$24 B =6 \times 1000 m =6000 m$

$B =\dfrac{6000}{24} m =250 m$

So,the length of the field $=2 \times 250 m =500 m$

28. Three squares are joined together as shown in Fig. 6.14. Their sides are $4 cm ; 10 cm$ and $3 cm $. Find the perimeter of the figure.

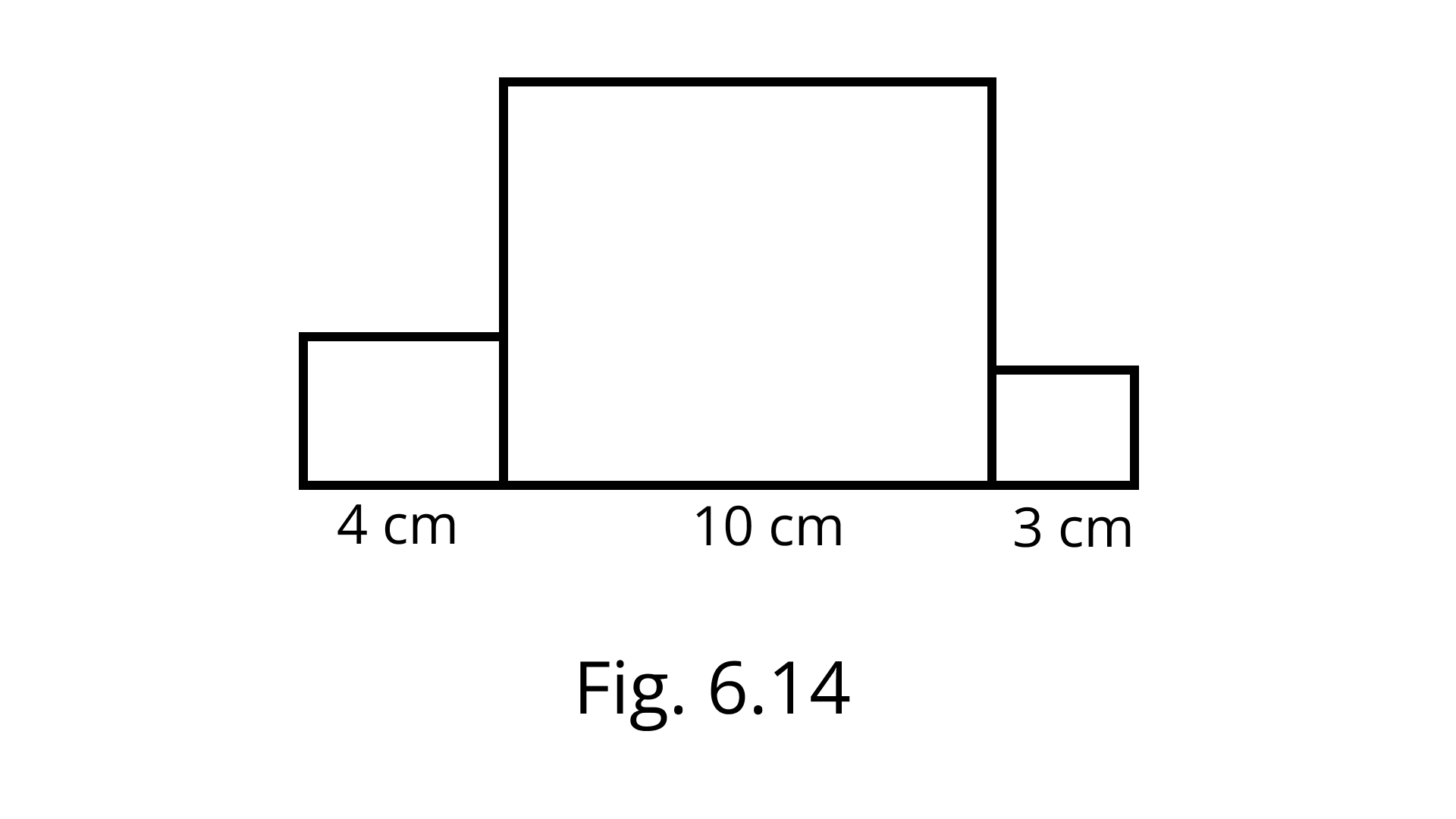
Ans:

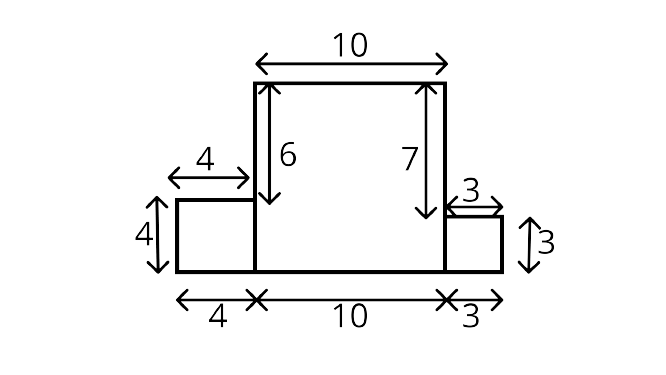
We know Perimeter = sum of all sides

Perimeter $=10+6+4+4+4+10+3+3+3+7=54cm$

29. In Fig. 6.15 all triangles are equilateral and $A B=8$ units. Other triangles have been formed by taking the midpoints of the sides. What is the perimeter of the figure.

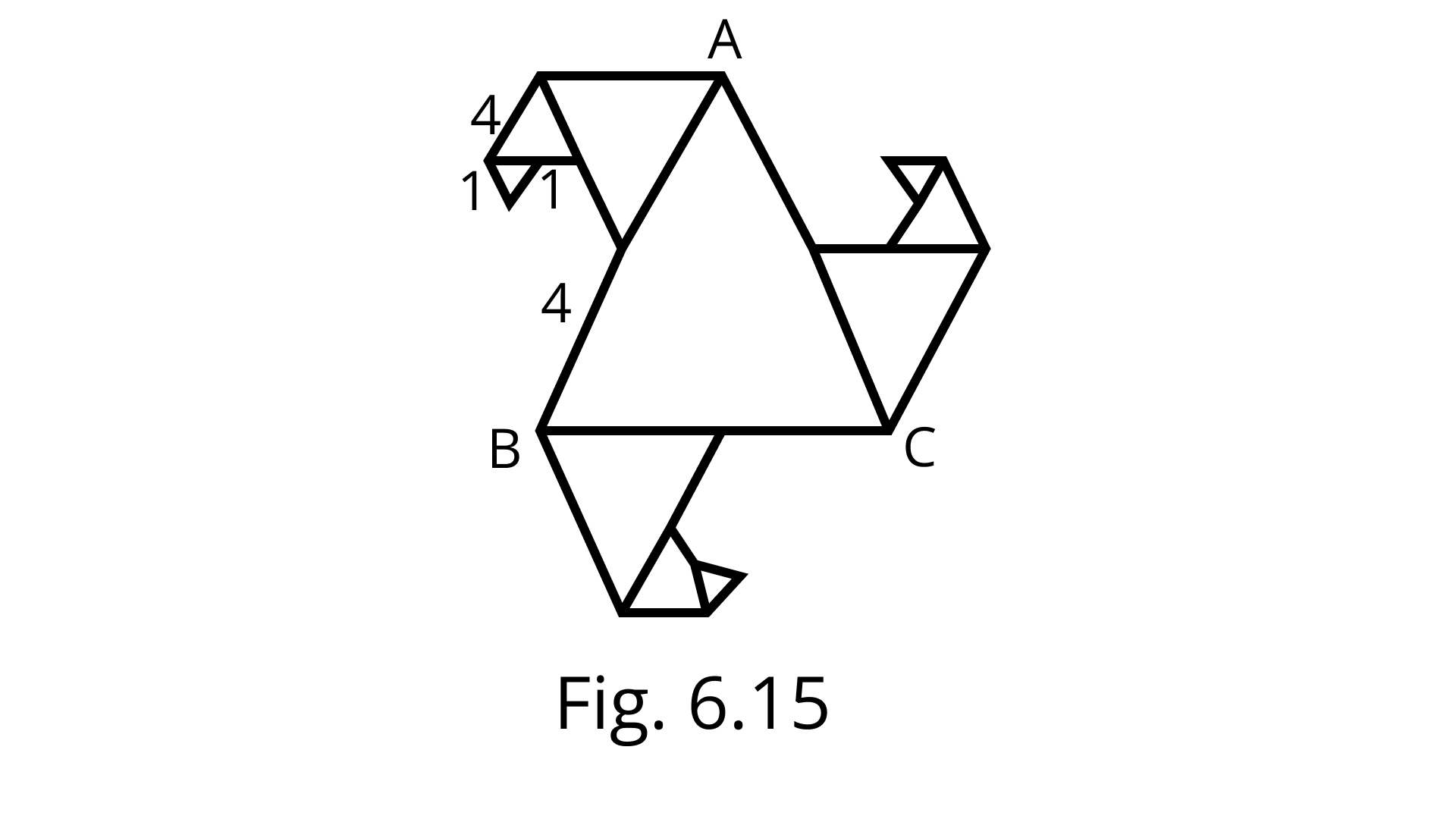
Ans: Given, all the triangle are equilateral and $AB =8$ unit

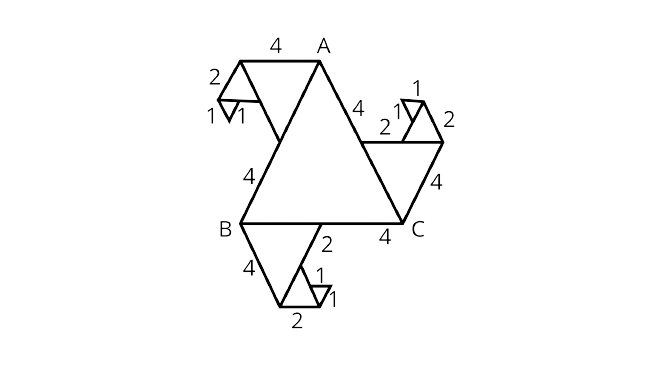
We know Perimeter = sum of all sides

Perimeter $=4+2+1+1+1+2+4+4+2+1+1+1+2+4+4+2+1+1+1+2+4$=$45$ units

30. The length of a rectangular field is $250 m$ and the width is $150 m$. Anuradha runs around this field 3 times. How far did she run? How many times should she run around the field to cover a distance of $4 km$ ?

Ans: Given, length $(l)=250 m$

and width $(b)=150 m$

Than,perimeter of the field $=2(l+b)=2(250+150) m =2 \times 400 m =800 m$

Because distance covered in one round $=$ Perimeter $=800 m$

So,distance covered in three rounds $=3 \times 800=2400 m$

Now, number of rounds to cover $4 km$ =$\dfrac{4000}{800}=5$

$[\because 1 km =1000 m ]$

So, she should run 5 times around the field to cover the distance of $4 km$.

31. Bajinder runs ten times around a square track and covers $4 km$. Find the length of the track.

Ans: Given,length of track covered in 10 rounds $=4 km =4000 m [\therefore 1 km =1000 m ]$

So,length of track covered in 1 round $=\dfrac{4000}{10}=400 m$

Perimeter of square = $ 4 \times$ side

So length of track = $\dfrac{400}{4}=100m$

32. The lawn in front of Molly's house is $12 m \times 8 m$,whereas the lawn in front of Dolly's house is $15 m \times 5 m$. Bamboo fencing is built around both the lawns. How much fencing is required for both?

Ans: Perimeter of the lawn in front of Molly's house

$=2 \times(\text { L }+\text {B })$

$2 \times(12+8) =2 \times 20 =40 m$

Perimeter of the lawn in front of Dolly's house

$=2 \times(\text { L }+\text { B })$

$2 \times(15+5)  =2 \times 20  =40 m$

So,Fencing is required for both $=40 +40 =80 m$

33. The perimeter of a regular pentagon is $1540 cm$. How long is it's every side?

Ans: Given,the perimeter of a regular pentagon=$1540 cm$

We know Perimeter = sum of all sides

Perimeter of the regular pentagon=$5 \times$ length of sides $=1540 cm$

Sides $=\dfrac{1540}{5} cm =308 cm$

So,length of the side of the regular pentagon is $308 cm$.

34. The perimeter of a triangle is $28 cm$. One of its sides is $8 cm$. Write all the sides of the possible isosceles triangles with these measurements.

Ans: Given,the perimeter of a triangle =$28 cm$ 

Let sides of a triangle are x,y and z

than $x= y$,$z=8 cm$

We know Perimeter = sum of all sides =$28 cm$

$x+y+z=28$

$x+x+8=28$

$2x=28-8$

$x=\dfrac{20}{2}$

$x=10cm$

Sides are $10cm,10cm$ and $8cm$

Let sides of a triangle are x,y and z

And $x=y=8cm$

We know Perimeter = sum of all sides =$28 cm$

$x+y+z=28$

$8+8+z=28$

$16+z=28$

$z=28-16$

$z=12cm$

Sides are $8cm,8cm$ and $12cm$

35. The length of an Aluminium strip is $40 cm$. If the lengths in $cm$ are measured in natural numbers, write the measurement of all the possible rectangular frames which can be made out of it. (For example, a rectangular frame with $15 cm$ length and $5 cm$ breadth can be made from this strip.)

Ans: Perimeter of rectangular frame $=$ Length of the aluminum strip

$2 \times($ length $+$ breadth $)=40 cm$

Length + Breadth = 20 cm

∴ The possible measurement of rectangular frames are 1 cm $\times$ 19 cm, 2 cm $\times$ 18 cm, 3 cm $\times$ 17 cm, 4 cm $\times$ 16 cm, 5 cm $\times$ 15 cm, 6 cm $\times$ 14 cm, 7 cm $\times$ 13 cm, 8 cm $\times$ 12 cm, 9 cm $\times$ 11 cm, 10 cm $\times$ 10 cm

36. The base of a tent is a regular hexagon of perimeter $60 cm$. What is the length of each side of the base?

Ans: Perimeter of hexagon $=6 \times$ sides $=60 cm$

$\text { Side }=\dfrac{60}{6} =10 cm$

So, each side of the base is $10 cm$.

37. In an exhibition hall, there are 24 display boards each of length $1 m 50 cm$ and breadth $1 m$. There is a $100 m$ long aluminium strip, which is used to frame these boards.

How many boards will be framed using this strip? Find also the length of the aluminium strip required for the remaining boards.

Ans: Length $=1 m 50 cm =1.5 m$

Breadth $=1 m$

Than,perimeter of one display board= $2 \times($ length $+$ breadth $)$

$2 \times(1.5 m +1 m )$

$2 \times 2.5 m =5 m$

So,perimeter of the display board =$5 \times 24=120 m$

Number of boards framed $=\dfrac{100}{5}=20$

And length of the aluminum strip required for the remaining boards $=(120-100) m =20 m$

38. In the above question, how many square meters of cloth are required to cover all the display boards? What will be the length in $m$ of the cloth used, if its breadth is $120 cm$ ?

Ans: Length $=1 m 50 cm =1.5 m$

Breadth $=1 m$

Area of the display board

$24 \times($ length $\times$ breadth $)=24 \times 1.5 m \times 1 m =36 m ^{2}$

$36 m ^{2}$ cloths are needed to cover all the display boards.

Now, breadth of the cloth $=120 cm =\dfrac{120}{100} m =1.2 m$

$[\therefore 1 m =100 cm ]$

So,length of the cloth $=\dfrac{\text { area }}{\text { breadth }}=\dfrac{36 m ^{2}}{1.2 m }=30 m$

39. What is the length of the outer boundary of the park shown in Figure, what will be the total cost of fencing it at the rate of Rs 20 per meter? There is a rectangular flower bed in the centre of the park. Find the cost of manuring the flower bed at the rate of Rs $5 0$ per square meter.

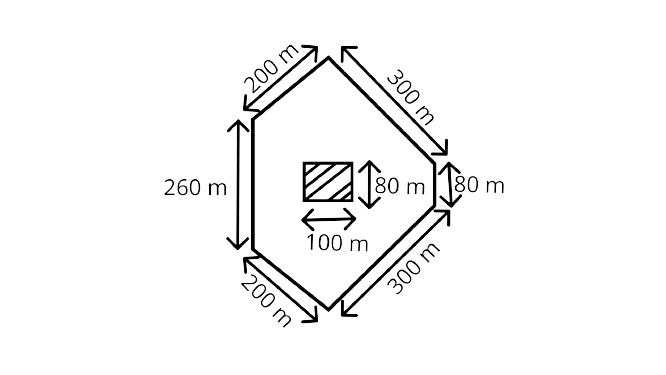
Ans: We know Perimeter = sum of all sides

Perimeter $=(200+300+80+300+200+260) m=1340 m$

Than,rate of  fencing it at the rate of Rs 20 per meter

$=$ Rs. $(1340 \times 20)=$ Rs. 26800

Area of the flower bed $=(100 \times 80) m ^{2}=8000 m ^{2}$

Also,rate of manuring the flower bed per square metre= Rs 50 per square meter

Than,rate of manuring the flower bed per 8000 square meter $=$ Rs. $(50 \times 8000)=$ Rs. 400000

40. Total cost of fencing the park shown in Figure is Rs 55000. Find the cost of fencing per meter.

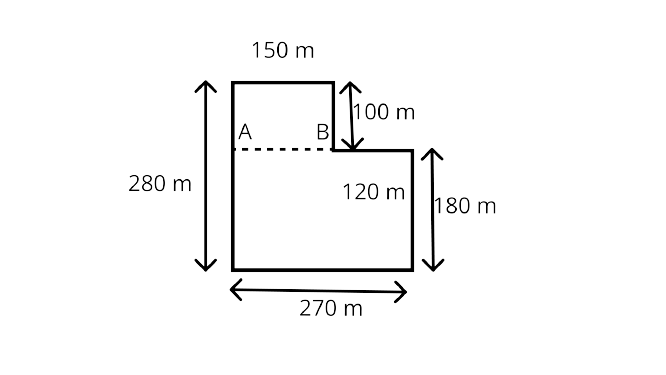
Ans: We know Perimeter = sum of all sides

Perimeter  $=150+100+120+180+270+280$=$1100 m$

Now cost of fencing the per meter$=\dfrac{\text { Total cost of fencing }}{\text { Perimeter of the park }}=\text { Rs. }\left(\dfrac{55000}{1100}\right)=\text { Rs.50 }$

41. In Figure  each square is of unit length

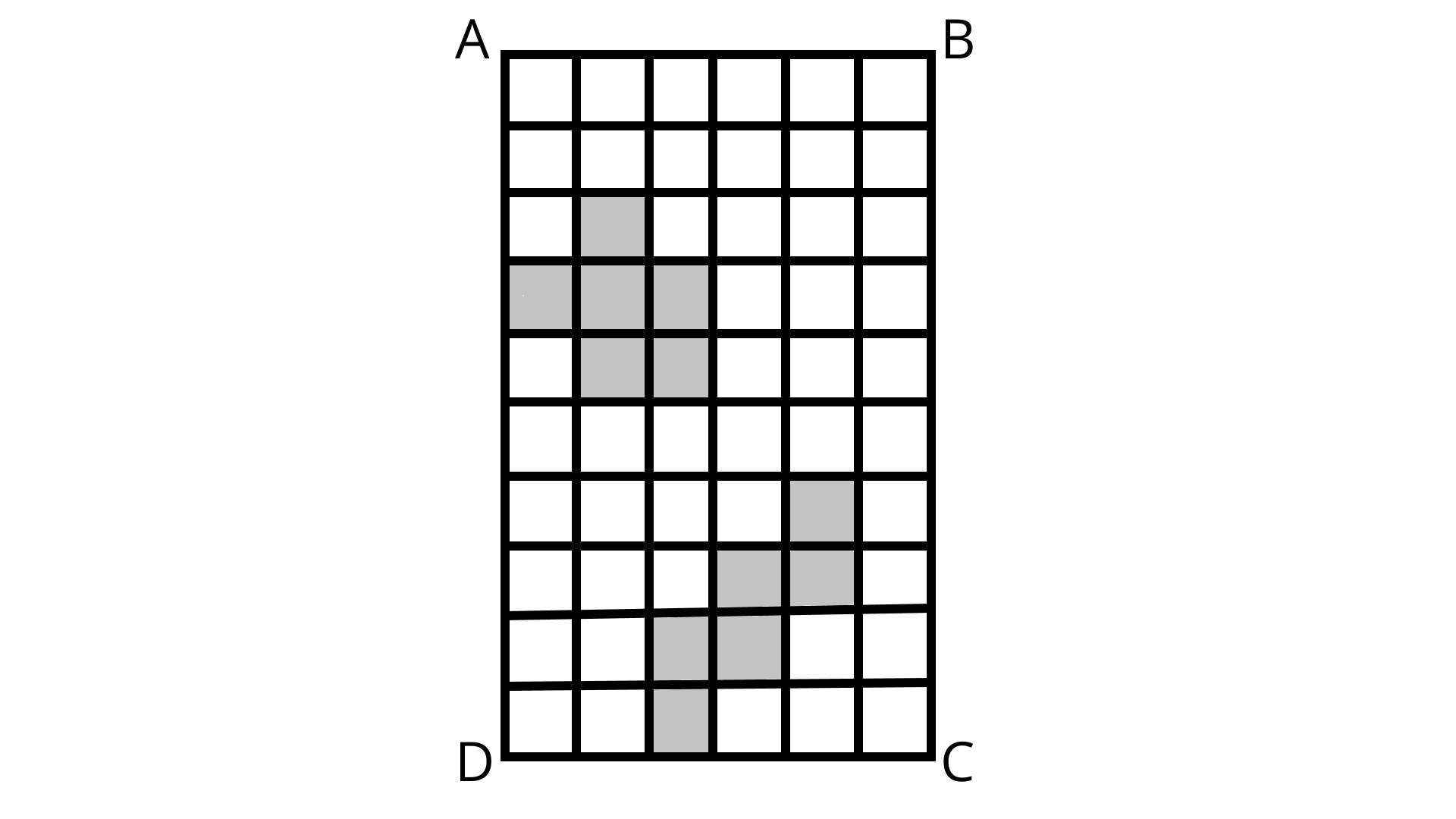
(a) What is the perimeter of the rectangle ABCD?

Ans:Given that each square is of unit length,$ABCD$ is 10 units and breadth is 6 units

Perimeter of $ABCD = 2 \times($ length $+$ breadth $)$

$=2 \times(10+6)$ units $=2 \times 16$ units $=32$ units

(b) What is the area of the rectangle $A B C D$ ?

Ans:Area of rectangle $ABCD =$ length $\times$ breadth

$(10 \times 6) \text { units }^{2}=60 \text { units }^{2}$

(c) Divide this rectangle into ten parts of the equal area by shading squares.

(Two parts of equal area are shown here)

Ans: The figure shows the part of the rectangle of the equal area by shading squares 1,2, 3, 4, 5, 6, 7, 8, 9 and 10.

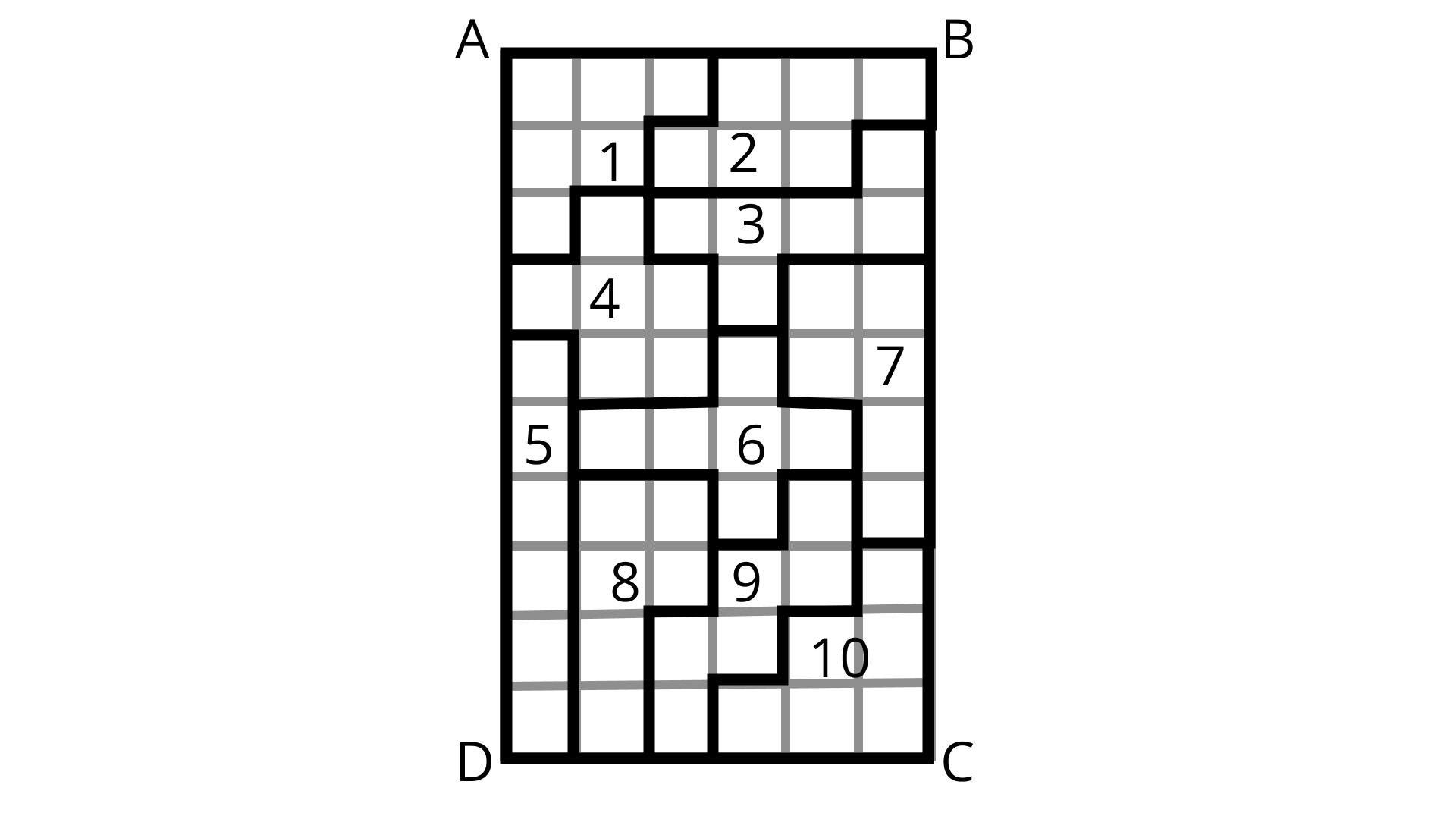
(d) Find the perimeter of each part which you have divided. Are they all equal?

Ans: For 1,2,4,7,8 & 10 parts, Perimeter is 12 units.

For 3,5,6 & 9 Perimeter is 14 units.

No, they are not equal.

42. Rectangular wall MNOP of a kitchen is covered with square tiles of $15 cm$ length ( in Figure). Find the area of the wall.

Ans: Area of square tile=$15\times 15$=225$cm^{2}$

Number of tile $=28$ square 

So, area of the wall $=(225 \times 28) cm ^{2}$ $=6300 cm ^{2}$

43. The length of a rectangular field is 6 times its breadth. If the length of the field is $120 cm$, find the perimeter of the field. 

Ans: Given,Length ($L$)=120cm and breadth=$B$

Than,L=$6 B$ 

$B =\dfrac{120}{6} =20 cm$ 

Perimeter of the rectangle $=2 \times( L + B )$ 

$2 \times(120+20) =2 \times 140  =280 cm$

44. Anmol has a chart paper measuring $90 cm \times 40 cm$, whereas Abhishek has one which measures $50 cm \times 70 cm .$ Which will cover more area on the table and by how much? 

Ans: The area of the Anmol's chart paper =$(90 cm \times 40 cm )=3600 cm ^{2}$ 

The area of the Abhishek's chart paper= $(50 cm \times 70 cm )=3500 cm ^{2}$ 

So,Anmol will cover more area on the table and by how 100 cm $^{2}$. 

45. A rectangular path of $60 m$ length and $3 m$ width is covered by square tiles of side $25 cm$. How many tiles will there be in one row along its width? How many such rows will be there? Find the number of tiles used to make this path?

Ans: Given length ($L) =60 m =6000 cm$

Width($B)=3 m =300 cm$

Side of the square tile $=25 cm$

Number of tiles in one row along width

$\dfrac{\text { width of the path }}{\text { side of the a tile }}=\dfrac{300}{25}=12$

$\text {Number of the rows}=\dfrac{\text {length of the path}}{\text{side of a tile }}=\dfrac{6000}{25}=240$

Number of tiles=$12\times 240=2880$

46. How many square slabs each with side $90 cm$ are needed to cover a floor of area 81sqm.

Ans: Given,side of square slab=90cm

Area of square slab $=(90 cm )^{2}=8100 cm ^{2}$

And,area of the floor$=81 m ^{2}=81 \times 10000 cm ^{2}$

$=810000 cm ^{2}$

Number of slab=$\dfrac{\text { Area of the floor }}{\text { Area of square slab }}$

$=\dfrac{810000}{8100}=100 \text { slabs }$

47. The length of a rectangular field is $8 m$ and breadth is $2 m$. If a square field has the same perimeter as this rectangular field, find which field has the greater area.

Ans: Given,length(L)=8m

Width(B)=2m

Than,perimeter=$2(L+B)$=$2(8+2)=2\times 10=20m$

And,area=$L \times B$=$8 \times 2$=$16m^{2}$

According to the question

Perimeter=Perimeter of a rectangular

$4\times Side$=20

$Side=\dfrac{20}{4}$=$5m$

Now,area of square=$Side\times Side$=$5\times 5=25m^{2}$

Hence,the area of a square field is greater than the area of a rectangular field.

48. Parminder walks around a square park once and covers $800 m$. What will be the area of this park?

Ans: Given , perimeter of the square $=800 m =4 \times$ sides

$800 m =4 \times \text { sides }$

$\text { side }=\dfrac{800}{4} =200 m$

And area of square $=Side\times Side=(200 m )^{2}=40000 m ^{2}$

49. The side of a square is $5 cm$. How many times does the area increase, if the side of the square is doubled?

Ans: Given,side of square  $=5 cm$

Than,area of square $=Side\times Side=5\times 5=25 cm ^{2}$....(i)

According to the question

New side=$2\times old  side$

$=2\times 5=10cm$

Now,area of square $=10\times 10=100 cm ^{2}$

By,(i) and (ii) area of the new square is increased by 4 times.

50. Amita wants to make rectangular cards measuring $8 cm$ $\times 5 cm$. She has a square chart paper of $60 cm$. How many complete cards can she make from this chart? What area of the chart paper will be left?

Ans: Given,area of square chart=$60\times 60=3600cm^{2}$

Length of the chart is $60 cm$ and in that 7 cards of 8 cm length she can make and for width $60 cm$ she can make exactly 12 cards of length 5cm.

So total no. of cards $= 12 \times 7 =84$

And area of card=$8\times 5=40cm^{2}$

The area of left part of square chart$=3600 -(84\times 40)=240cm^{2}$

51. A magazine charges Rs 300 per $10 sqcm$ area for advertising. A company decided to order a half-page advertisement. If each page of the magazine is $15 cm \times$ $24 cm$, what amount will the company has to pay for it?

Ans: Area of one page of the magazine $=15 cm \times 24 cm =360$ $cm ^{2}$

Than,area of half page of the magazine $=\dfrac{360}{2} cm ^{2}=180 cm ^{2}$

Cost of advertising for $10 cm ^{2}=$ Rs.300

Cost of advertising for $1 cm ^{2}=\dfrac{Rs.300}{10}$

Cost of advertising for $180 cm ^{2}$=$\text { Rs. } \dfrac{300}{10} \times 180$

$=\text { Rs. } 30 \times 180=\text { Rs. } 5400$

52. The perimeter of a square garden is $48 m$. A small flower bed covers the $18 sqm$ area inside this garden. What is the area of the garden that is not covered by the flower bed? What fractional part of the garden is covered by the flower bed? Find the ratio of the area covered by the flower bed and the remaining area.

Ans: Given perimeter of the square garden $=48 m =4 \times$ side

$\text { side }=\dfrac{48}{4} =12 m$

Now,area of square garden$=Side\times Side=12\times 12=144 m ^{2}$

Also,given area of small flower bed $=18 m ^{2}$

Than,area of the garden not covers with flower bed$=144-18=126 m ^{2}$

Now,the fractional part of the garden covered by the flower bed $=\dfrac{\text { Area of flower bed }}{\text { Area of the square garden }}=\dfrac{18}{144}=\dfrac{1}{8}$

In addition,the ratio of the area covered by the flower bed and the remaining area $=\dfrac{18}{126}=\dfrac{1}{7} \quad$ i.e. $1: 7$

53. The perimeter of a square and a rectangle is the same.If a side of the square is $15 cm$ and one side of the rectangle is $18 cm$, find the area of the rectangle.

Ans: Given,side of the square = $15 cm$ ,length of the rectangle=$18 cm$

According to the question

Also given,perimeter of the square $=$ perimeter of the rectangle=$4 \times \text { sides }=2 \times(\text { length }+\text { breadth })$

$4 \times 15  =2 \times(18  + breadth )$

$60 =2 \times(18 + breadth )$

$breadth =30-18 =12 cm$

Now,area of the rectangular $=18 \times 12=216 cm ^{2}$

Area of square =${15}^{2}cm ^{2}=225cm ^{2}$

54. A wire is cut into several small pieces. Each of the small pieces is bent into a square of side $2 cm$. If the total area of the small squares is 28 square $cm$, what was the original length of the wire?

Ans:Given,square of side= $2 cm$

Length of one piece $=$ Perimeter of the square $=4 \times 2 cm =8 cm$

Let the number of pieces = $n$

According to the question

$n \times(\text { side })^{2}=28$

$n \times(2)^{2}=28$

$n=\dfrac{28}{4}=7$

The original length of the wire $=\text { Number of pieces } \times \text { length of one piece }$

$=7 \times 8=56 cm$

55. Divide the park shown in Fig. 14 of question 40 into two rectangles. Find the total area of this park. If one packet of fertilizer is used for $300 sqm$, how many packets of fertilizer are required for the whole park?

Ans: 

Total area of the park $=(150 \times 100)+(270 \times 180)$

$=15000+48600=63600 m ^{2}$

Now one packet of fertilizer used for area $=300 m ^{2}$

Than, number of total packets$=\dfrac{63600}{300}$ $=212$

56. The area of a rectangular field is $1600 sqm$. If the length of the field is $80 m$, find the perimeter of the field.

Ans: Given, area of a rectangular field $=1600 m ^{2}$

And length $=80 m$

Now, area $=length \times breadth$

$80 \times breadth =1600$

$breadth =\dfrac{1600}{80}$

$=20 m$

Now, perimeter of rectangular field $=2(length+breadth)$

$=2(80+20)=200 m$

57. The area of each square on a chess board is $4 sqcm$. Find the area of the board.

(a) At the beginning of the game when all the chess men are put on the board, write the area of the squares left unoccupied.

Ans: Given,the area of the square on a chess board $=4cm^{2}$

There are 64 squares on a chess board.

So,area of the chess board $=64 \times 4 sq cm =256 cm ^{2}$

Area of the squares left unoccupied in the beginning$=32 \times$ area of  a square$=32 \times 4 =128 cm ^{2}$

(b) Find the area of the squares occupied by chess men.

Ans: Area of the squares occupied by chessmen$=32 \times$ area of one square$=32 \times 4=128 cm ^{2}$

58. (a) Find all the possible dimensions (in natural numbers) of a rectangle with a perimeter $36 cm$ and find their areas.

Ans: Perimeter of the rectangle $=36 cm$

$2 \times(\text { length }+\text { breadth })=36 cm$

$(\text { length }+\text { breadth })=\dfrac{36}{2}=18 cm$

Than,the possible dimension of the rectangle and their area as follows:

(b) Find all the possible dimensions (in natural numbers) of a rectangle with an area of $36 sqcm$, and find their perimeters.

Ans: Area of a rectangle =$length\times  breadth$=$36cm^{2}$

Than,the possible dimension of the rectangle and their area as follows:

59. Find the area and perimeter of each of the following figures,if the area of each small square is 1sqcm.

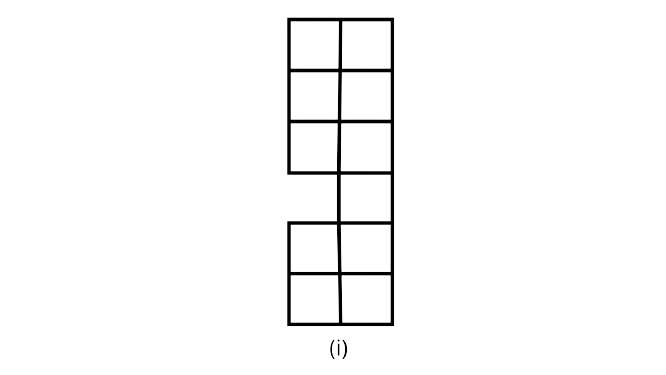
Ans: Given,area of each small square =$1{cm}^{2}$

And there are 11 small squares.

So, area =$11\times 1=11{cm}^{2}$

Perimeter=sum of all sides

Perimeter=18cm

Ans: Given,area of each small square = $1cm^{2}$

And there are 13 small squares.

So, area =$13\times 1=13cm^{2}$

Perimeter=sum of all sides

Perimeter=28cm

Ans: Given,area of each small square = $1cm^{2}$

And there are 13 small squares.

So, area =$13\times 1=13cm^{2}$

Perimeter=sum of all sides

Perimeter=28cm

60 . What is the area of each small square in the Figure if the area of the entire figure is $96 sqcm$. Find the perimeter of the figure.

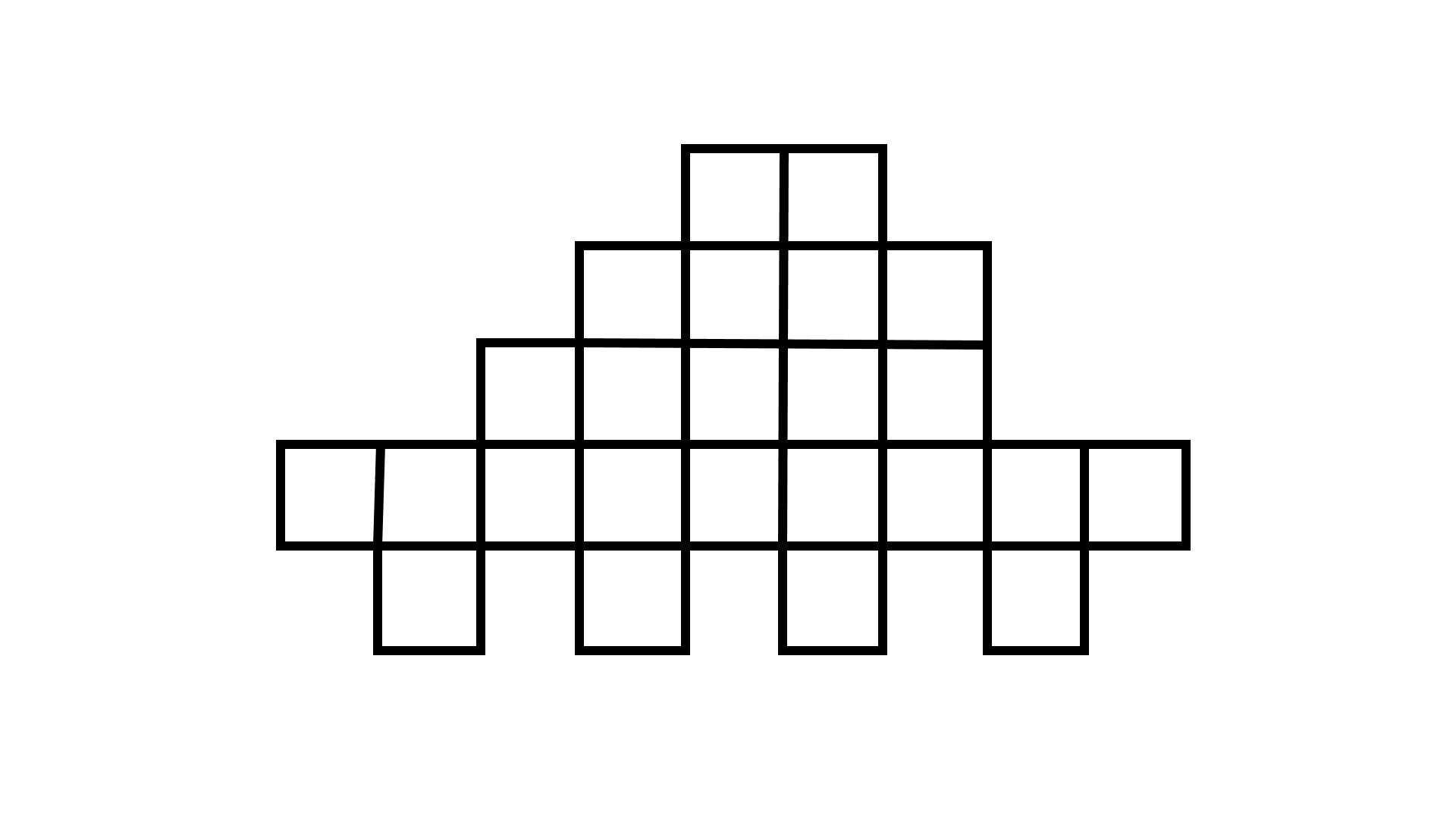
Ans: Given,area of the figure $=96 cm ^{2}$

Total no. of small square in the given figure $=24$

So, area of each small square $=\dfrac{96}{24}$$=4 cm ^{2}$

Now, side of each small square $=2 cm$

Perimeter of the figure $=34 \times 2$$=68 cm$

Class 6 Chapter 6 Mensuration Maths NCERT Exemplar

NCERT exemplar of Class 6 support students to prepare topics of Mensuration and remaining ones. In the examination, several questions come from the exemplar.

Mensuration teaches you about the concept of perimeter and area of the plane figure. Perimeter is the total distance covered along the boundary of that particular shape or figure. The area is the total amount of surface enclosed by the plane figure.

In this Chapter, three plane figures, i.e. Triangle, Square, Rectangle, are added.

You can download the unsolved Class 6 maths exemplar from the official site of NCERT.  NCERT provides all types of resources like textbooks, examples etc., for free.

How to Download Solutions of NCERT Class 6 Mensuration Exemplar Solutions

NCERT Exemplar comes without solutions. And questions included in it are different from the ones available in the textbook. To check your answers, you can download solutions of all subjects exemplar from our website.

Download solutions of the Class 6 Mensuration questions of the exemplar from the given link. Experts have provided these solutions to help you get a proper understanding of the topics. You can download this solution after signing in with your email id or current mobile number. Vedantu provides other resources like important Chapters notes, textbook solutions. For online maths tuition, register now and learn from the best teachers.