Question

How do you write \[y=3{{x}^{2}}-12x+1\] in vertex form?

Answer 1

Hint: We are given a quadratic equation which we have to write in the vertex form. We will first take \[3\] common from \[3{{x}^{2}}\] and \[12x\]. Then, the expression will look like \[y=3({{x}^{2}}- 4x)+1\]. Next, we will use completing the square method and compute the corresponding equation and obtain the resulting equation in the form \[y=a{{(x-h)}^{2}}+k\], which is the vertex form.

Complete step by step solution:
According to the given question, we have to find the vertex form of the given quadratic equation.
We can say that the vertex form of the quadratic equation can be given as,
\[y=a{{(x-h)}^{2}}+k\]
where \[(h,k)\]is the vertex
and as we can see there is an ‘a’ in the vertex form which similar to the one in the quadratic
equation, that is, \[y=a{{x}^{2}}+bx+c\].

We have the given equation as,
\[y=3{{x}^{2}}-12x+1\]----(1)
We will take \[3\] common from \[3{{x}^{2}}\] and \[12x\], we get,
\[\Rightarrow y=3({{x}^{2}}-4x)+1\]
Then, we will use the completing the square method and convert it to the vertex form.
We will add and subtract 4 within the bracket, we have,
\[\Rightarrow y=3({{x}^{2}}-4x+4-4)+1\]
\[\Rightarrow y=3({{x}^{2}}-4x+4)-4(3)+1\]
We know that \[{{x}^{2}}-4x+4={{(x-2)}^{2}}\], we will have the new expression as,
\[\Rightarrow y=3{{(x-2)}^{2}}-12+1\]
Next, we have,
\[\Rightarrow y=3{{(x-2)}^{2}}-11\]
\[\Rightarrow y=3{{(x-2)}^{2}}+(-11)\]
This is in the vertex form, similar to the \[y=a{{(x-h)}^{2}}+k\].
And the vertex is \[(2,-11)\].

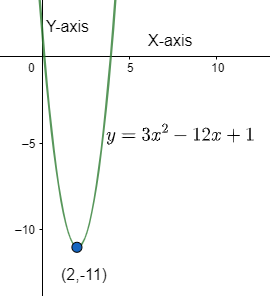
Therefore, the vertex form of the given equation is \[y=3{{(x-2)}^{2}}+(-11)\].

Note: The quadratic equation should be computed step wise to the vertex form. While carrying out the completing square method, the value added should be subtracted as well, so that the overall expression is not changed.