Question

Write the value of ${{\cos }^{-1}}\left( \cos \dfrac{7\pi }{6} \right)$ .

Answer 1

Hint: For solving this question first, we will go through some important aspects like domain and range of the inverse trigonometric function $y={{\cos }^{-1}}x$ . First, we will use one of the basic formula of the trigonometric ratio to write $\cos \dfrac{7\pi }{6}=-\dfrac{\sqrt{3}}{2}$ in the given term. After that, we will use one of the basic formula of inverse trigonometric functions, i.e. ${{\cos }^{-1}}\left( -\dfrac{\sqrt{3}}{2} \right)=\dfrac{5\pi }{6}$ for giving the final answer for the question correctly.

Complete step-by-step solution -
Given:
We have to find the value of the following term:
${{\cos }^{-1}}\left( \cos \dfrac{7\pi }{6} \right)$
Now, before we proceed we should know about the inverse trigonometric function $y={{\cos }^{-1}}x$ . For more clarity look at the figure given below:

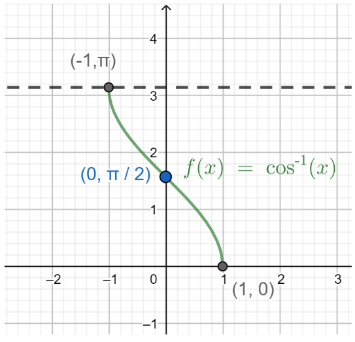
In the above figure, the plot $y=f\left( x \right)={{\cos }^{-1}}x$ is shown. And we should know that the function $y={{\cos }^{-1}}x$ is defined for $x\in \left[ -1,1 \right]$ and its range is $y\in \left[ 0,\pi \right]$ then, $y$ is the principal value of ${{\cos }^{-1}}x$ .
Now, we will use the above concept for giving the correct value of ${{\cos }^{-1}}\left( \cos \dfrac{7\pi }{6} \right)$ .
Now, before we proceed further we should know the following formulas:
$\begin{align}
  & \cos \dfrac{7\pi }{6}=\cos \left( \pi +\dfrac{\pi }{6} \right)=-\cos \dfrac{\pi }{6}=-\dfrac{\sqrt{3}}{2}..................\left( 1 \right) \\
 & {{\cos }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right)=\dfrac{\pi }{6}...........\left( 2 \right) \\
 & {{\cos }^{-1}}\left( -x \right)=\pi -{{\cos }^{-1}}x\text{ }\left( \text{if 0}\le \text{x}\le \text{1} \right)..............\left( 3 \right) \\
\end{align}$
Now, we will use the above two formulas to solve this question.
We have, ${{\cos }^{-1}}\left( \cos \dfrac{7\pi }{6} \right)$ .
Now, we will use the formula from the equation (1) to write $\cos \dfrac{7\pi }{6}=-\dfrac{\sqrt{3}}{2}$ in the term ${{\cos }^{-1}}\left( \cos \dfrac{7\pi }{6} \right)$ . Then,
$\begin{align}
  & {{\cos }^{-1}}\left( \cos \dfrac{7\pi }{6} \right) \\
 & \Rightarrow {{\cos }^{-1}}\left( -\dfrac{\sqrt{3}}{2} \right) \\
\end{align}$
Now, as $0<\dfrac{\sqrt{3}}{2}<1$ so, we will use the formula from the equation (3) to write ${{\cos }^{-1}}\left( -\dfrac{\sqrt{3}}{2} \right)=\pi -{{\cos }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right)$ in the above line. Then,
$\begin{align}
  & {{\cos }^{-1}}\left( -\dfrac{\sqrt{3}}{2} \right) \\
 & \Rightarrow \pi -{{\cos }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right) \\
\end{align}$
Now, we will use the formula from the equation (2) to write ${{\cos }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right)=\dfrac{\pi }{6}$ in the above equation. Then,
$\begin{align}
  & \pi -{{\cos }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right) \\
 & \Rightarrow \pi -\dfrac{\pi }{6} \\
 & \Rightarrow \dfrac{5\pi }{6} \\
\end{align}$
Now, from the above result, we conclude that the value of the expression ${{\cos }^{-1}}\left( \cos \dfrac{7\pi }{6} \right)$ will be equal to $\dfrac{5\pi }{6}$ . Then,
${{\cos }^{-1}}\left( \cos \dfrac{7\pi }{6} \right)=\dfrac{5\pi }{6}$
Now, as it is evident that $\dfrac{5\pi }{6}$ lies in the range of the function $y={{\cos }^{-1}}x$ so, value of ${{\cos }^{-1}}\left( \cos \dfrac{7\pi }{6} \right)=\dfrac{5\pi }{6}$ .
Thus, ${{\cos }^{-1}}\left( \cos \dfrac{7\pi }{6} \right)=\dfrac{5\pi }{6}$ .

Note: Here, the student should first understand what is asked in the question and then proceed in the right direction to get the correct answer quickly. And we should avoid writing ${{\cos }^{-1}}\left( \cos \dfrac{7\pi }{6} \right)=\dfrac{7\pi }{6}$ directly and use the basic concepts of domain and range of the inverse trigonometric function $y={{\cos }^{-1}}x$ correctly. Moreover, as we know that, $\cos \dfrac{5\pi }{6}=-\dfrac{\sqrt{3}}{2}$ and $0<\dfrac{5\pi }{6}<\pi $ so, we can directly write ${{\cos }^{-1}}\left( -\dfrac{\sqrt{3}}{2} \right)=\dfrac{5\pi }{6}$ by the formula ${{\cos }^{-1}}\left( \cos \theta \right)=\theta $ if $\theta \in \left[ 0,\pi \right]$ . And after giving the final answer, we should check for the validity of our answer by checking whether it lies in the range of the function $y={{\cos }^{-1}}x$.