Question

Write the length of an arc of a sector of a circle with radius $r$ and angle with degree measure $\theta $.

Answer 1

Hint: Assume that for $360{}^\circ $ the circumference of the circle is $2\pi r$, where $r$ is the length of the radius of the circle. Then find the length of the arc for $1{}^\circ $ and finally find the length of the arc of angle $\theta $.

Complete step-by-step answer:
In the question we have been asked to find the length of an arc of a sector of a circle with radius $r$ and an angle with degree measure $\theta $. We will first explain what an arc and sector of a circle is. An arc of a circle is a portion of the circumference of the circle. The length of an arc is simply the length of its portion of the circumference. A circular sector /circle sector is the portion of a disk enclosed by two radii and an arc, where the smaller area is known as the minor sector and the larger one as the major sector.

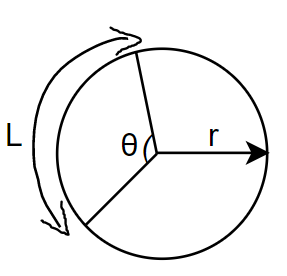
In the above figure, L is the length of the arc of the angle $\theta $ of the circle and the region is called as the sector of the circle. Now, as we know that the length of circumference of the entire circle is $2\pi r$, where $r$ is the radius of the circle. The total angles contained in a circle is $2\pi $ or $360{}^\circ $.
So, for angle $360{}^\circ $ the length of the circumference is $2\pi r$.
So, for angle $1{}^\circ $ the length of the arc would be $\dfrac{2\pi r}{360}$.
And for angle $\theta $ the length of the arc would be $\dfrac{\theta }{360}\times 2\pi r$.
Hence the length of an arc of a sector of the circle would be $\dfrac{\theta }{360}\times 2\pi r$.

Note: When it was a full circle, the term circumference was used, but when an angle $\theta $ is taken, then it is considered as an arc because an arc is the length of the curved side of the circle, while circumference refers to the perimeter, which means that it consists the length of the radius too.