Question

Write the formula of the angle of minimum deviation produced by a thin prism.

Answer 1

Hint: Start by using the equation of prism \[\mu = \dfrac{{\sin \left[ {\dfrac{{(A + D)}}{2}} \right]}}{{\sin \dfrac{A}{2}}}\] . Since the angles are small \[\sin \left( {\dfrac{{A + D}}{2}} \right) = \dfrac{{A + D}}{2}\] and \[\sin \left( {\dfrac{A}{2}} \right) = \dfrac{A}{2}\] the equation now becomes \[D = A\left( {\mu - 1} \right)\] . Then use the snell’s law \[\mu = \dfrac{{\sin i}}{{\sin {r_1}}}\] and since angles are small \[\sin i = i\] , \[\sin {r_1} = {r_1}\] , \[\sin {r_2} = {r_2}\] and \[\sin e = e\] . Use these values to obtain the equation \[u \approx \dfrac{i}{{{r_1}}}\] and \[\mu \approx \dfrac{e}{{{r_2}}}\] . Then use simple geometry to obtain the equation \[(i + e) - \left( {{r_1} + {r_2}} \right) = \angle D\] . Then put the value \[{r_1} + {r_2} = \angle A\] in the previous equation to reach the solution.

Complete answer:
The angle of deviation is the angle that the emerging ray coming out of a prism makes with the incident ray coming in the prism (indicated as angle D in the diagram below). This angle of deviation decreases with an increase in the angle of incidence, but only up to a minimum angle called the angle of minimum deviation (indicated by \[{D_m}\] ).

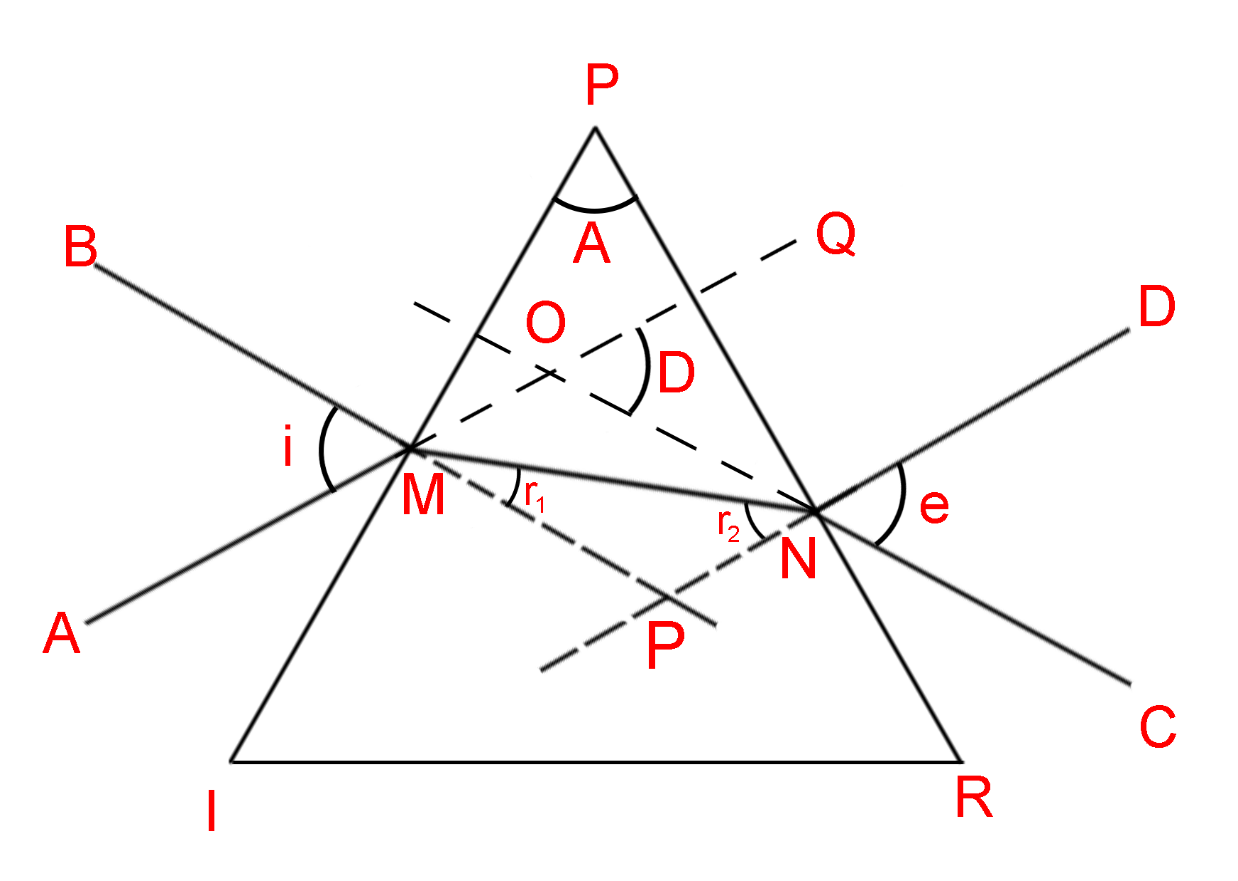
The refractive index of the material of the prism is calculated by using the following formula
\[\mu = \dfrac{{\sin \left[ {\dfrac{{(A + D)}}{2}} \right]}}{{\sin \dfrac{A}{2}}}\] (Equation 1)
\[\mu = \] The refractive index of the material of the prism
\[A = \] The angle of the prism
\[D = \] Angle of deviation
For thin prisms or small angle prisms, as the angles become very small, the sine of the angle nearly equals the angle itself, i.e. \[\sin \left( {\dfrac{{A + D}}{2}} \right) = \dfrac{{A + D}}{2}\] and \[\sin \left( {\dfrac{A}{2}} \right) = \dfrac{A}{2}\] .
Putting these values in equation 1, we get
\[\mu \approx \dfrac{{\left( {\dfrac{{A + D}}{2}} \right)}}{{\left( {\dfrac{A}{2}} \right)}}\]
\[\mu = \dfrac{{A + D}}{A}\]
\[\mu A = A + D\]
\[D = A\left( {\mu - 1} \right)\]
Now, for the angle of minimum deviation this equation becomes
\[{D_m} = A\left( {\mu - 1} \right)\]
We know by Snell’s law for the incident ray
\[\mu = \dfrac{{\sin i}}{{\sin {r_1}}}\]
Since the angles are small, so \[\sin i = i\] and \[\sin {r_1} = {r_1}\] .
So, \[u \approx \dfrac{i}{{{r_1}}}\]
We know by Snell’s law for the emergent ray
\[\dfrac{1}{\mu } = \dfrac{{\sin {r_2}}}{{\sin e}}\]
\[\mu = \dfrac{{\sin e}}{{\sin {r_2}}}\]
Since the angles are small, so \[\sin e = e\] and \[\sin {r_2} = {r_2}\] .
So, \[\mu \approx \dfrac{e}{{{r_2}}}\]
We know,
\[\angle AMB = \angle OMP = i\] (Vertically opposite Angles)
\[\angle CND = \angle PNO = e\] (Vertically opposite angles)
In \[\Delta OMN\] ,
\[\angle OMN + \angle MNO = \angle QON\] ( \[\angle QON\] is an external angle to the triangle \[\Delta OMN\] )
\[(\angle OMP - \angle NMP) + (\angle PNO - \angle MNP) = \angle QON\]
\[i - {r_1} + e - {r_2} = \angle D\]
\[(i + e) - \left( {{r_1} + {r_2}} \right) = \angle D\] (Equation 1)
In \[\Delta PMN\] the sum of all the angles is \[180^\circ \]
\[\angle OMN + \angle MNO + \angle MPN = 180^\circ \]
\[(90^\circ - \angle NMP) + \left( {90^\circ - \angle MNP} \right) + \angle A = 180^\circ \]
\[\left( {90^\circ - {r_1}} \right) + \left( {90^\circ - {r_2}} \right) + \angle A = 180\]
\[{r_1} + {r_2} = \angle A\]
Substituting this value in equation 1, we get
\[\left( {i + e} \right) - \left( {\angle A} \right) = \angle D\]
For, the angle of minimum deviation, \[i = e\] , so equation 2 becomes
\[2i - \angle A = \angle {D_{\min }}\]
\[i = \dfrac{{A + {D_{\min }}}}{2}\]

Note:
The prism is optical equipment that is used to observe the dispersion of white light. The prism makes use of the fact that light travels with different speeds in different mediums. The prism is normally made out of glass, the edges of the prism should be perfect during the manufacturing of the glass prisms.