Question

Which one of the following statements is true?
A) $ \cos \left( {A + B} \right) = \cos A + \cos B $
B) $ \cos \left( {A + B} \right) = \cos A\cos B $
C) $ \cos \left( {A + B} \right) = \cos A\cos B - \sin A\sin B $
D) $ \cos \left( {A + B} \right) = \cos A\cos B + \sin A\sin B $

Answer 1

Hint: In this question, we need to find which of the above given statements is true. For this, we will consider a rotating line in an anti-clockwise direction, which makes acute angles $ a $ and $ b $ . By which we will construct a diagram and we will find the angles of the points. And use the formula of $ \sin \theta $ and $ \cos \theta $ to find which of the above statements are true.

Complete step-by-step answer:
Let a rotating line $ OX $ rotate about $ O $ in the anti-clockwise direction. From starting position to its initial position $ OX $ making an acute angle $ a $ . And again, the rotating line rotates further in the same direction and starting from position $ OY $ and makes out an acute angle $ b $ .
To understand this concept, let us construct a figure.
First draw a horizontal line $ X $ (the x-axis) and mark the origin $ O $ . Next, draw a line $ Y $ from $ O $ at an angle $ a $ above the horizontal line $ X $ and in the similar way, draw a second line $ Z $ at an angle $ b $ above that. Such that, the angle between the line $ Z $ and the x-axis is $ a + b $ . Here, $ a $ and $ b $ are positive acute angles and $ a + b < 90^\circ $ .
Mark the point $ P $ in the line $ Z $ (which is defined by the angle $ a + b $ ) at a unit distance from the origin.
Let $ PQ $ be a line, perpendicular to the line $ OQ $ defined by angle $ a $ , which is drawn from point $ Q $ on this line to point $ P $ . Therefore, $ OQP $ forms a right angle.
Let $ QA $ be a perpendicular from point $ A $ on the x-axis to $ Q $ and $ PB $ be a perpendicular from point $ B $ on the x-axis to $ P $ . Therefore, $ OAQ $ and $ OBP $ are right angles.
Now, draw $ R $ on $ PB $ such that $ QR $ is parallel to the x-axis.

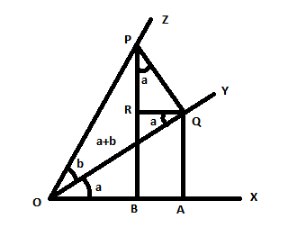
From the diagram, $ OQA = \dfrac{\pi }{2} - a $
Then, $ RQO = a $
 $ \Rightarrow $ $ RQP = \dfrac{\pi }{2} - a $
Then, $ RPQ = a $
Therefore, $ RPQ = \dfrac{\pi }{2} - RQP $
 $ = \dfrac{\pi }{2} - \left( {\dfrac{\pi }{2} - RQO} \right) $
= $ RQO $
= $ a $
Now from the right-angled triangle $ POB $ , we get,
 $ \cos (a + b) = \left( {\dfrac{{OB}}{{OP}}} \right) $
 $ = \dfrac{{OA - BA}}{{OP}} $
 $ = \dfrac{{OA}}{{OP}} - \dfrac{{BA}}{{OP}} $
 $ = \dfrac{{OA}}{{OP}} - \dfrac{{RQ}}{{OP}} $
 $ = \dfrac{{OA}}{{OQ}}.\dfrac{{OQ}}{{OP}} - \dfrac{{RQ}}{{PQ}}.\dfrac{{PQ}}{{OP}} $
We know that,
 $ \sin \theta = \dfrac{{Opposite}}{{Hypotenuse}} $
And, $ \cos \theta = \dfrac{{Adjacent}}{{Hypotenuse}} $
By using the above formula, we get,
 $ \cos \left( {a + b} \right) = \cos a\cos b - \sin a\sin b $
Hence, option C) $ \cos \left( {A + B} \right) = \cos A\cos B - \sin A\sin B $ is the true statement.
So, the correct answer is “Option C”.

Note: In this question, be careful in applying the formula of $ \sin \theta $ and $ \cos \theta $ when using the diagram. In similar way, we can find the values of $ \sin \left( {a + b} \right) $ , $ \sin \left( {a - b} \right) $ and $ \cos \left( {a - b} \right) $ . We can also use complementary angle formulae i.e., $ \sin \theta = \cos \left( {\dfrac{\pi }{2} - \theta } \right) $ and $ \cos \theta = \sin \left( {\dfrac{\pi }{2} - \theta } \right) $ to determine $ \cos \left( {a + b} \right) $ . Here, consider $ \theta = \left( {a + b} \right) $ and apply it in the formula of $ \cos \theta $ and solve it.