Question

What is the wavelength of a photon emitted during a transition from $n = 5$ state to $n = 2$ state in the hydrogen atom?
A. $434\;nm$
B. $450\;nm$
C. $350\;nm$
D. $525\;nm$

Answer 1

Hint: The photon emitted during the transition from any state to $n = 2$ state lies on Balmer series of transition. When there is a transition between the two states in a hydrogen atom, the relation between the number of the states and the wavelength is given by the Rydberg equation for hydrogen atom. By using that relation, the wavelength of the photon can be calculated.

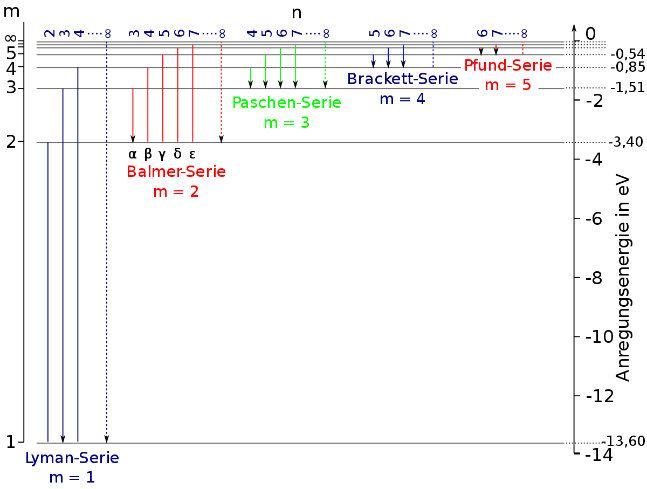
Useful formula:
The Rydberg equation for hydrogen atom is given by,
$\dfrac{1}{\lambda } = {R_H}\left[ {\dfrac{1}{{{n_1}^2}} - \dfrac{1}{{{n_2}^2}}} \right]$
Where, $\lambda $ is the wavelength of the emitted photon, ${R_H}$ is the Rydberg constant of hydrogen, ${n_2}$ is the initial state of transition and ${n_1}$ is the final state of transition.

Complete step by step solution:
Given, The final state of transition, ${n_1} = 2$
The initial state of transition, ${n_2} = 5$
The Rydberg constant of hydrogen, ${R_H} = 10973731.6\;{m^{ - 1}}$

The Rydberg equation for hydrogen atom is given by,
$\dfrac{1}{\lambda } = {R_H}\left[ {\dfrac{1}{{{n_1}^2}} - \dfrac{1}{{{n_2}^2}}} \right]\;.....................................\left( 1 \right)$
Substitute the given values of ${n_1}$, ${n_2}$ and ${R_H}$ in the equation (1),
$
  \dfrac{1}{\lambda } = 10973731.6\;{m^{ - 1}}\left[ {\dfrac{1}{{{2^2}}} - \dfrac{1}{{{5^2}}}} \right] \\
  \dfrac{1}{\lambda } = 10973731.6\left[ {\dfrac{1}{4} - \dfrac{1}{{25}}} \right] \\
  \dfrac{1}{\lambda } = 10973731.6\left[ {0.25 - 0.04} \right] \\
  \dfrac{1}{\lambda } = 10973731.6\left[ {0.21} \right] \\
  \dfrac{1}{\lambda } = 2304483.636\;{m^{ - 1}} \\
    \\
 $
Taking reciprocal on both sides,
$
  \lambda = \dfrac{1}{{2304483.636\;{m^{ - 1}}}} \\
  \lambda = 4.3393 \times {10^{ - 7}}\;m \\
 $
Convert unit from $m$ to $nm$,
$1\;m = {10^9}\;nm$
Hence,
$
  \lambda = 4.3393 \times {10^{ - 7}}\;m\; \times \dfrac{{{{10}^9}\;nm}}{{1\;m}} \\
  \lambda = 4.3393 \times {10^2}\;nm \\
  \lambda = 433.93\;nm \\
  \lambda \simeq 434\;nm \\
 $
Hence, the wavelength of photon emitted during transition, $\lambda = 434\;nm$

Thus, the option (A) is correct.

NOTE:
Alternative method:
Hint: The energy level of photons in each level are calculated by using the energy formula for each state. Then the difference in the energy is obtained by taking the difference between two energies. And by using the Planck-Einstein relation the frequency of the emitted photon can be calculated and with the help of the relation between speed of light, wavelength and frequency of light, the wavelength can be obtained.

Useful formula:
The energy of hydrogen in each state is given by,
${E_n} = - \dfrac{{13.6\;eV}}{{{n^2}}}\;Joules$
Where, $ - 13.6\;eV$ is the approximate ground state energy of the hydrogen atom and $n$ is the state.
The Planck-Einstein relation is given by,
$E = h \times \upsilon $
Where, $E$ is the energy difference, $h$ is the Planck’s constant and $\upsilon $ is the frequency of the photon.
The relation between speed of light, wavelength and frequency of light is given by,
$c = \lambda \times \upsilon $
Where, $c$ is the speed of photon or light, $\lambda $ is the wavelength of photon and $\upsilon $ is the frequency of photon.

Complete step by step solution:
Given, The final state of transition, ${n_1} = 2$
The initial state of transition, ${n_2} = 5$
Planck’s constant, $h = 6.626 \times {10^{ - 34}}\;J.s$
Speed of photon, $c = 3 \times {10^8}\;\dfrac{m}{s}$
Step by step solution:
The energy of hydrogen in $n = 5$ state,
$
  {E_5} = - \dfrac{{13.6\;eV}}{{{5^2}}} \\
  {E_5} = - \dfrac{{13.6}}{{25}} \\
  {E_5} = - 0.544\;eV \\
 $
Convert $eV$ to $J$,
$1\;eV = 1.602 \times {10^{ - 19}}\;J$
Hence,
$
  {E_5} = - 0.544 \times 1.602 \times {10^{ - 19}}\;J \\
  {E_5} = - 0.871 \times {10^{ - 19}}\;J \\
  {E_5} = - 8.71 \times {10^{ - 20}}\;J \\
 $
The energy of hydrogen in $n = 2$ state,
$
  {E_2} = - \dfrac{{13.6\;eV}}{{{2^2}}} \\
  {E_2} = - \dfrac{{13.6}}{4} \\
  {E_2} = - 3.4\;eV \\
 $
Convert $eV$ to $J$,
$1\;eV = 1.602 \times {10^{ - 19}}\;J$
Hence,
$
  {E_2} = - 3.4 \times 1.602 \times {10^{ - 19}}\;J \\
  {E_2} = - 5.44 \times {10^{ - 19}}\;J \\
 $
Difference in energy between $n = 5$ state and $n = 2$ state,
$\Delta E = {E_2} - {E_5}\;...............................\left( 2 \right)$
Substitute the values of ${E_2}$ and ${E_5}$ in equation (2),
$
  \Delta E = \left( { - 5.44 \times {{10}^{ - 19}}\;J} \right) - \left( { - 8.71 \times {{10}^{ - 20}}\;J} \right) \\
  \Delta E = 4.57 \times {10^{ - 19}}\;J \\
 $
The Planck-Einstein relation is given by,
$\Delta E = h \times \upsilon \;...........................\left( 3 \right)$
Substitute the values of $\Delta E$, $h$ and $\upsilon $ in equation (3),
$
  4.57 \times {10^{ - 19}}\;J = 6.626 \times {10^{ - 34}}\;Js\; \times \upsilon \\
  \upsilon = \dfrac{{4.57 \times {{10}^{ - 19}}\;J}}{{6.626 \times {{10}^{ - 34}}\;Js}} \\
  \upsilon = 6.897 \times {10^{14}}\;{s^{ - 1}} \\
 $
The relation between speed of light, wavelength and frequency of light is given by,
$c = \lambda \times \upsilon \;.................................\left( 4 \right)$
Substitute the values of $c$and $\upsilon $ in equation (4),
$
  3 \times {10^8}\;m{s^{ - 1}} = \lambda \times 6.897 \times {10^{14}}\;{s^{ - 1}} \\
  \lambda = \dfrac{{3.8 \times {{10}^8}\;m{s^1}}}{{6.897 \times {{10}^{14}}\;{s^{ - 1}}}} \\
  \lambda = 4.354 \times {10^{ - 7}}\;m \\
 $
Convert unit from $m$ to $nm$,
$1\;m = {10^9}\;nm$
Hence,
$
  \lambda = 4.35 \times {10^{ - 7}}\;m\; \times \dfrac{{{{10}^9}\;nm}}{{1\;m}} \\
  \lambda = 4.35 \times {10^2}\;nm \\
  \lambda = 435\;nm \\
  \lambda \simeq 434\;nm \\
 $

Hence, the option (A) is correct.

These two methods are used to find the wavelength of the photon emitted from one state to another state. In the first method the Rydberg equation is directly used to find the wavelength and in the second method, the energy equation, Planck-Einstein equation and relation between speed, wavelength and frequency of photon are used. Bothe these methods give the approximate answer of wavelength.