
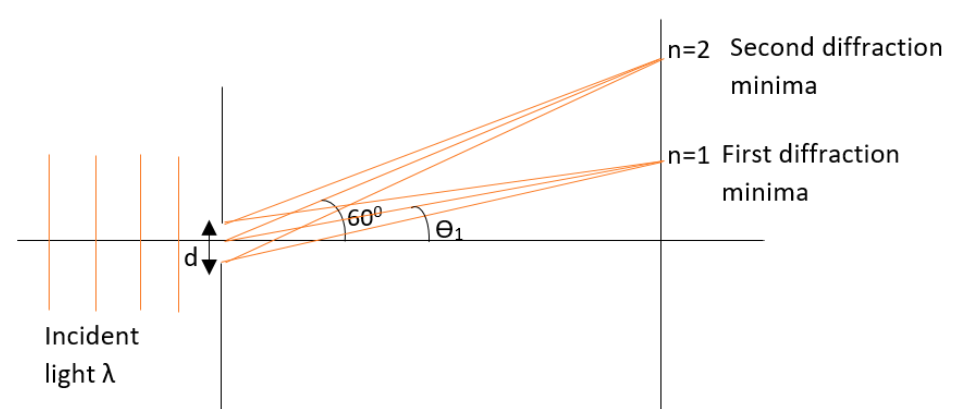
Visible light of wavelength $6000\times {{10}^{-8}}cm$ falls normally on a single slit and develops a diffraction pattern. It is found that the second diffraction minimum is at $60{}^\circ $ from the central maximum. If the first minimum is created at ${{\theta }_{1}}$, then ${{\theta }_{1}}$ will be close to?
Answer
571.8k+ views
Hint: For the diffraction minima to occur, the product of the order of the patterns formation and the wavelength of the light will be equal to the product of slit width and the sine of the angle at which first minimum is produced. Using this relation, find the slit width of the arrangement for the second minimum. Similarly find the angle for the first diffraction also. These all may help you to solve this question.
Complete step by step answer:
For a diffraction minima to occur, the product of the order of the patterns formation and the wavelength of the light will be equal to the product of slit width and the sine of the angle at which first minimum is produced. That is, we can write that,
$n\lambda =d\sin \theta $
Where $d$ be the slit width, $\lambda $be the wavelength of the light, $\theta $ be the angle of diffraction minimum and $n$ be the order of the minima.
Here it has been mentioned that the wavelength of the light used is,
$\lambda =6000\times {{10}^{-8}}cm$
Therefore for the first condition,
The second diffraction minima has been produced. Hence we can write that,
$n=2$
And the angle between the central maxima and the second diffraction minima will be,
$\theta =60{}^\circ $
Substituting this in the equation,
$\begin{align}
& 2\lambda =d\sin 60{}^\circ \\
& d=\dfrac{2\lambda }{\sin 60{}^\circ }=\dfrac{4\lambda }{\sqrt{3}} \\
\end{align}$
Therefore the slit width has been obtained.
Now in the second condition,
The first minima has been produced,
$n=1$
Substituting the values accordingly in the equation will give,
$\begin{align}
& 1\lambda =d\sin {{\theta }_{1}} \\
& \sin {{\theta }_{1}}=\dfrac{\lambda }{d} \\
\end{align}$
Now let us substitute the values of slit width in it.
$\sin {{\theta }_{1}}=\dfrac{\lambda }{\dfrac{4\lambda }{\sqrt{3}}}=\dfrac{\sqrt{3}}{4}$
From this the angle will be,
${{\theta }_{1}}={{\sin }^{-1}}\dfrac{\sqrt{3}}{4}\approx 25{}^\circ $
Note: In the single-slit diffraction, the bending phenomenon of light or diffraction occurs that causes light from a coherent source to interfere with itself and develops a distinctive pattern on the screen. This pattern is called a diffraction pattern. There will be minima and maxima in the pattern. Maxima is the portion of higher intensity and minima is the portion of smaller intensity.
Complete step by step answer:
For a diffraction minima to occur, the product of the order of the patterns formation and the wavelength of the light will be equal to the product of slit width and the sine of the angle at which first minimum is produced. That is, we can write that,
$n\lambda =d\sin \theta $
Where $d$ be the slit width, $\lambda $be the wavelength of the light, $\theta $ be the angle of diffraction minimum and $n$ be the order of the minima.
Here it has been mentioned that the wavelength of the light used is,
$\lambda =6000\times {{10}^{-8}}cm$
Therefore for the first condition,
The second diffraction minima has been produced. Hence we can write that,
$n=2$
And the angle between the central maxima and the second diffraction minima will be,
$\theta =60{}^\circ $
Substituting this in the equation,
$\begin{align}
& 2\lambda =d\sin 60{}^\circ \\
& d=\dfrac{2\lambda }{\sin 60{}^\circ }=\dfrac{4\lambda }{\sqrt{3}} \\
\end{align}$
Therefore the slit width has been obtained.
Now in the second condition,
The first minima has been produced,
$n=1$
Substituting the values accordingly in the equation will give,
$\begin{align}
& 1\lambda =d\sin {{\theta }_{1}} \\
& \sin {{\theta }_{1}}=\dfrac{\lambda }{d} \\
\end{align}$
Now let us substitute the values of slit width in it.
$\sin {{\theta }_{1}}=\dfrac{\lambda }{\dfrac{4\lambda }{\sqrt{3}}}=\dfrac{\sqrt{3}}{4}$
From this the angle will be,
${{\theta }_{1}}={{\sin }^{-1}}\dfrac{\sqrt{3}}{4}\approx 25{}^\circ $

Note: In the single-slit diffraction, the bending phenomenon of light or diffraction occurs that causes light from a coherent source to interfere with itself and develops a distinctive pattern on the screen. This pattern is called a diffraction pattern. There will be minima and maxima in the pattern. Maxima is the portion of higher intensity and minima is the portion of smaller intensity.
Recently Updated Pages
The number of solutions in x in 02pi for which sqrt class 12 maths CBSE

Write any two methods of preparation of phenol Give class 12 chemistry CBSE

Differentiate between action potential and resting class 12 biology CBSE

Two plane mirrors arranged at right angles to each class 12 physics CBSE

Which of the following molecules is are chiral A I class 12 chemistry CBSE

Name different types of neurons and give one function class 12 biology CBSE

Trending doubts
State the principle of an ac generator and explain class 12 physics CBSE

Sketch the electric field lines in case of an electric class 12 physics CBSE

Derive an expression for electric potential at point class 12 physics CBSE

What is virtual and erect image ?

Explain the formation of energy bands in solids On class 12 physics CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




