Question

Verify Euler’s formula for these solids.

Answer 1

Hint: First of all recall the definition of vertices, edges and faces of a solid figure. Then, count the number of faces, the number of edges and the number of vertices in the given figures. Next, apply the Euler’s formula in the given figure, which is [Number of faces+ Number of vertices- Number of edges =2]. We have to verify if the result holds true for both the given figures.

Complete step by step solution: We have to prove the Euler’s formula for the given figures.
We will first find the number of vertices, the number of edges and number of faces in the given figures to apply the Euler’s formula.
As we know that any solid figure can be defined using the number of combination of its edges, vertices and faces.
Let us first recall the definition of the basic components of a solid figure, that are, vertices, edges and faces.

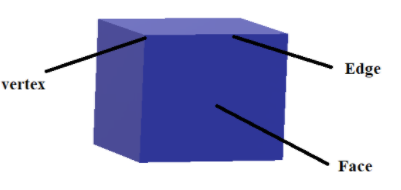
Vertices in a solid figure are the meeting points of two or more lines.
Edges are the line segments where two faces meet.
Faces are the flat surfaces enclosed by the edges in a solid figure.
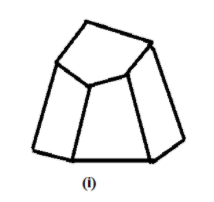
In figure (i), we can see that there are 7 faces, 10 vertices and 5 edges.
We know that Euler’s formula for solid figure says that the [Number of faces+ Number of vertices- Number of edges =2]
Let us now substitute the value of Number of faces, the number of vertices and number of edges for the figure (i) in Euler’s formula.
Hence, we have
$7 + 10 - 15$
On solving the above expression, we get,
$17 - 15 = 2$
Hence, the Euler’s formula is verified for the figure (i)
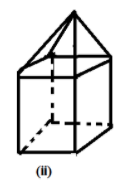
Now, for the figure (ii), we have 9 faces, 9 edges and 16 vertices.
Let us now substitute the value of Number of faces, the number of vertices and number of edges for the figure (ii) in Euler’s formula.
$9 + 9 - 16$
On solving the above expression, we get,
$18 - 16 = 2$
Thus, Euler’s formula is verified for the figure (ii).

Note: Euler’s formula holds true for every polyhedron, that is a closed shape which has flat surfaces and straight edges. Euler’s formula does not work for the shapes with holes or when the opposite faces intersect together at a common point. Here, visualisation of the figure is important to determine the correct number of faces, edges and vertices in the given figure.