Question

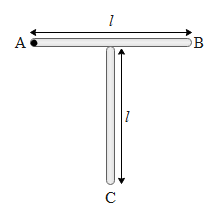
Two uniform rods are welded together to form letter T as shown in the figure. Each rod is of mass M and length L. If this combination is hinged at A and kept in vertical plane then the time period of small oscillation about A is equal to

a)$2\pi \sqrt{\dfrac{l}{6\sqrt{3}g}}$
b)$2\pi \sqrt{\dfrac{3l}{2\sqrt{2}g}}$
c)$2\pi \sqrt{\dfrac{l}{2g}}$
d)$2\pi \sqrt{\dfrac{11l}{6\sqrt{5}g}}$

Answer 1

Hint: The above system is basically a compound pendulum. The T shaped system is hinged at A and can oscillate at small angles points B and C move downwards in the plane of the paper. Hence using the expression for the time period of compound pendulum we will determine the time period.
Formula used:
$T=2\pi \sqrt{\dfrac{{{I}_{system}}}{mg{{l}_{C.M}}}}$

Complete answer:
Let us say we have a compound pendulum having a combined moment of inertia along the axis about which it oscillates as ${{I}_{system}}$ . Let the effective mass of the system be ‘M’ and the distance from the center of mass of the system to the axis of oscillation be ${{l}_{C.M}}$ . If the pendulum is kept under the action of gravity, then the time period of oscillation is given by,
$T=2\pi \sqrt{\dfrac{{{I}_{system}}}{Mg{{l}_{C.M}}}}$
If the two rods have mass m, then the effective mass will be equal to 2m. The centre of mass lies at a point of 3l/4 from point C. Therefore using Pythagoras theorem, the distance from the point A to center of mass i.e. ${{l}_{C.M}}$ is,
$\begin{align}
  & {{l}^{2}}_{C.M}={{(l/4)}^{2}}+{{(l/2)}^{2}} \\
 & {{l}^{2}}_{C.M}=\dfrac{20}{16\times 4}{{l}^{2}}=\dfrac{5}{16}{{l}^{2}} \\
 & \Rightarrow {{l}_{C.M}}=\dfrac{\sqrt{5}}{4}l....(1) \\
\end{align}$
Let the midpoint of rod AB be D. The moment of inertia at point A will be due to both the rods i.e. AB and DC. The moment of inertia due to rod AB is
${{I}_{AB}}=\dfrac{1}{3}m{{l}^{2}}$
Using the parallel axis theorem, the moment of inertia due to rod DC at A is,
${{I}_{DC}}=\dfrac{1}{12}m{{l}^{2}}+m{{(MA)}^{2}}$
Where MA is the distance between the center of mass of rod DC and A. Since DA=MD= l/2, using Pythagoras theorem $MA=\dfrac{l}{\sqrt{2}}$
Therefore the moment of inertia due to rod DC at point A is,
$\begin{align}
  & {{I}_{DC}}=\dfrac{1}{12}m{{l}^{2}}+m{{(MA)}^{2}} \\
 & \Rightarrow {{I}_{DC}}=\dfrac{1}{12}m{{l}^{2}}+m{{(\dfrac{l}{\sqrt{2}})}^{2}}=\dfrac{7}{12}m{{l}^{2}} \\
\end{align}$
Therefore the moment of inertia (${{I}_{system}}$ )at point A will be due to rod AB i.e. ${{I}_{AB}}$ and due to rod DC i.e.${{I}_{DC}}$ is numerically equal to,
$\begin{align}
  & {{I}_{system}}={{I}_{AB}}+{{I}_{DC}} \\
 & {{I}_{system}}=\dfrac{1}{3}m{{l}^{2}}+\dfrac{7}{12}m{{l}^{2}}=\dfrac{11}{12}m{{l}^{2}}....(2) \\
\end{align}$
Hence from equation 1 and 2, the time period of the above compound pendulum is,
$\begin{align}
  & T=2\pi \sqrt{\dfrac{{{I}_{system}}}{Mg{{l}_{C.M}}}} \\
 & \Rightarrow T=2\pi \sqrt{\dfrac{\dfrac{11}{12}m{{l}^{2}}}{2mg\left( \dfrac{\sqrt{5}}{4}l \right)}}=\sqrt{\dfrac{11l}{6\sqrt{5}g}} \\
\end{align}$

Therefore the correct answer of the above question is option d.

Note:
The parallel axis theorem states that the moment of inertia passing through any arbitrary axis on a body is equal to the sum of the moment of inertia along the center of mass and the product of mass times the square of the distance between the axis of consideration and the axis through center of mass. It is to be noted that the moment of inertia of the rod through its center of mass is $\dfrac{1}{12}m{{l}^{2}}$ . Using the parallel axis theorem moment of inertia at any point on the rod can be determined.