Question

Two sides of triangle are 13 cm and 14 cm and its semi perimeter is 18 cm find the third side of this triangle

Answer 1

Hint: The two sides and semi perimeter of the triangle are given, we can use the formula for the semi perimeter of a triangle and substitute the given values to find the value of the unknown side.
Perimeter of a triangle is the sum of it’s all the three sides and the semi perimeter is its half.

Complete step-by-step answer:
Let the sides of a triangle XYZ be x, y, and z
The value of two sides are given and the third is to be calculated, so:

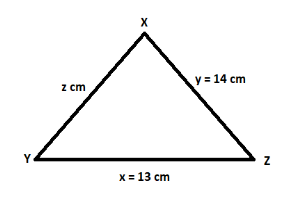
First side 🡪 x = 13 cm
Second side 🡪 y = 14 cm
Third side 🡪 z = z cm
Now, the perimeter of the triangle is sum of all the three sides given as:
P = x + y + z.
The semi perimeter is half the perimeter of the triangle, so it will be given as:
\[\Rightarrow {P_{semi}} = \dfrac{{x + y + z}}{2}\]
Substituting the values, we get:
\[\Rightarrow {P_{semi}} = \dfrac{{13 + 14 + z}}{2}\]
The value of semi perimeter is given as 18 cm, so:
\[\Rightarrow 18 = \dfrac{{13 + 14 + z}}{2}\]
Calculating the value of z:
\[
\Rightarrow 18 = \dfrac{{13 + 14 + z}}{2} \\
\Rightarrow 18 \times 2 = 27 + z \\
 \]
36 = 27 + z or
z + 27 = 36
z = 36 – 27
z = 9
All the sides are in cm, so this value of z will also be in cm.
z = 9 cm.
Therefore, the third side of the given triangle is 9 cm.

Note: A triangle comes under the category of a polygon (having more than one straight line connected) and the perimeter of all the polygons is the sum of their sides.
In an equilateral triangle all the sides are of equal length and hence its perimeter is:
3 X side.
In an isosceles triangle 2 sides are same and hence its perimeter is:
2 X side (that is same in both) + third side.
In a scalene triangle all the sides are different and hence its perimeter is:
Sum of all the three sides of different lengths.