Question

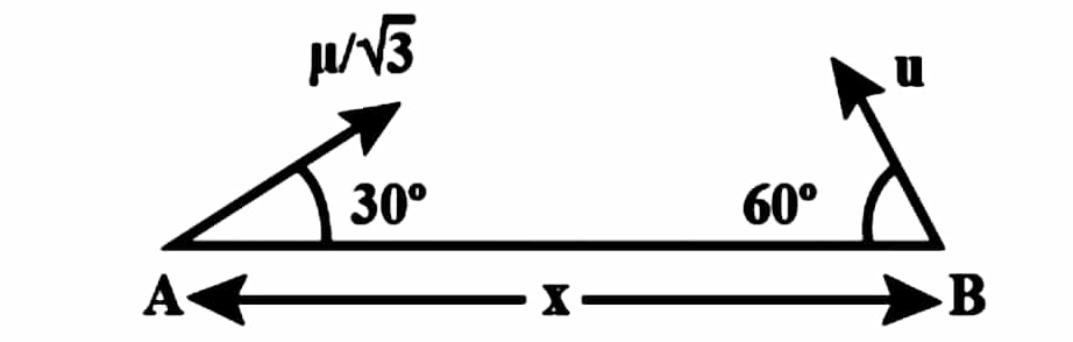
Two particles are separated at a horizontal distance x as shown in figure. They are projected at the same time with different initial velocity as shown in figure. Find the time when the horizontal distance between the particles is zero.

(A) $ t = 4x/u $
(B) $ t = 2x/u $
(C) $ t = x/u $
(D) $ t = 3x/u $

Answer 1

Hint :First find the horizontal velocity of both the objects. As we need to find time when horizontal distance is zero which is equal to time taken by an object moving with addition of speed of both objects and cover the given distance. Here we don’t need vertical velocity.

Complete Step By Step Answer:
Initial speed of first object is $ u/\sqrt 3 $ and make an angle of $ {30^0} $ with horizon as shown in figure, then its horizontal velocity is $ {v_1} = u/\sqrt 3 \times \cos {30^0} = \dfrac{u}{{\sqrt 3 }} \times \dfrac{{\sqrt 3 }}{2} = \dfrac{u}{2} $ .
Similarly, initial speed of first object is $ u $ and make an angle of $ {60^0} $ with horizon as shown in figure, then its horizontal velocity is $ {v_2} = u \times \cos {60^0} = u \times \dfrac{1}{2} = \dfrac{u}{2} $ .
We know that, when their horizontal distance is zero they cover a total distance of $ x $ and time taken is equal to taken by another object moving with speed equal to $ {v_1} + {v_2} $ and cover a distance of $ x $ .
We know that, $ {\text{time taken = }}\dfrac{{velocity}}{{{\text{distance}}}} $
Then, $ t = \dfrac{{{v_1} + {v_2}}}{x} $
Putting values of velocities in above equation, we get
 $ t = \dfrac{{\dfrac{u}{2} + \dfrac{u}{2}}}{x} = \dfrac{u}{x} $ .
Hence correct answer is option C.

Note :
We also solve this question using the concept of relative velocity. In the above solution we can see that horizontal speed of both objects are the same , meaning both cover half of the distance before they meet. And we just need time taken by either object to cover a distance $ x/2 $ .