Question

Two parallel chords 96cm and 28cm long are on the opposite side of the centre of the circle with radius 50cm. Find the area of the quadrilateral whose vertices are the endpoints of the chords.
(a) 3224 \[c{{m}^{2}}\]
(b) 3848 \[c{{m}^{2}}\]
(c) 3844 \[c{{m}^{2}}\]
(d) 3484 \[c{{m}^{2}}\]

Answer 1

Hint: Draw a diagram of the given situation. Construct perpendicular lines from the centre of the circle to the given chords. Use the theorem that ‘perpendicular line drawn from the centre of a circle to the chord bisects the chord’ and find the length of this perpendicular line using Pythagoras theorem given as: - \[{{h}^{2}}={{b}^{2}}+{{p}^{2}}\], where h = hypotenuse, b = base and p = perpendicular. Now, apply the formula for the area of trapezium given as: - Area = \[\dfrac{1}{2}\times \left( a+b \right)\times h\], to find the area of the quadrilateral. Here, a and b are the parallel sides and h is the distance between the parallel sides of the trapezium.

Complete step by step answer:
Let us draw a diagram of the given conditions.

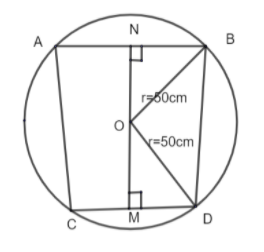
In the above figure we have assumed a circle with centre O. Here, AB and CD are two parallel chords of length 96cm and 28cm respectively. We have constructed OM and ON perpendicular to CD and AB respectively. The radius of the given circle is 50cm.
Now, we have to determine the area of quadrilateral ABCD. Since, two opposite sides AB and CD are parallel to each other, therefore ABCD can be assumed as a trapezium. To determine the area of trapezium we must find the distance between their parallel sides.
We know that perpendicular line from the centre of a circle to a chord bisects the chord. Therefore, OM and ON bisects the chords CD and AB respectively. So, applying this theorem, we get,
In right angle triangle ONB, we have,
OB = radius = 50cm
BN = \[\dfrac{1}{2}AB=\dfrac{1}{2}\times 96=48cm\]
Now, applying Pythagoras theorem, we get,
\[\Rightarrow {{h}^{2}}={{b}^{2}}+{{p}^{2}}\]
Here, h = hypotenuse = OB
b = base = BN
p = perpendicular = ON
\[\begin{align}
  & \Rightarrow O{{B}^{2}}=B{{N}^{2}}+O{{N}^{2}} \\
 & \Rightarrow {{50}^{2}}={{48}^{2}}+O{{N}^{2}} \\
 & \Rightarrow O{{N}^{2}}={{50}^{2}}-{{48}^{2}} \\
\end{align}\]
Applying the identity, \[{{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right)\], we get,
\[\begin{align}
  & \Rightarrow O{{N}^{2}}=\left( 50+48 \right)\left( 50-48 \right) \\
 & \Rightarrow O{{N}^{2}}=98\times 2 \\
 & \Rightarrow O{{N}^{2}}=196 \\
 & \Rightarrow O{{N}^{2}}=\sqrt{196}=14cm \\
\end{align}\]
Now, in right angle triangle OMD, we have,
OD = radius = 50cm
DM = \[\dfrac{1}{2}CD=\dfrac{1}{2}\times 28=14cm\]
Applying Pythagoras theorem, we get,
\[\Rightarrow {{h}^{2}}={{b}^{2}}+{{p}^{2}}\]
Here, h = hypotenuse = OD
b = base = DM
p = perpendicular = OM
\[\begin{align}
  & \Rightarrow O{{D}^{2}}=D{{M}^{2}}+O{{M}^{2}} \\
 & \Rightarrow {{50}^{2}}={{14}^{2}}+O{{M}^{2}} \\
 & \Rightarrow O{{M}^{2}}={{50}^{2}}-{{14}^{2}} \\
\end{align}\]
Applying the identity, \[{{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right)\], we get,
\[\begin{align}
  & \Rightarrow O{{M}^{2}}=\left( 50+14 \right)\left( 50-14 \right) \\
 & \Rightarrow O{{M}^{2}}=64\times 36 \\
\end{align}\]
\[\begin{align}
  & \Rightarrow O{{M}^{2}}={{8}^{2}}\times {{6}^{2}} \\
 & \Rightarrow OM=\sqrt{{{8}^{2}}\times {{6}^{2}}} \\
 & \Rightarrow OM=8\times 6=48cm \\
\end{align}\]
Now, we can clearly see that the distance between the chords AB and CD is MN.
\[\begin{align}
  & \Rightarrow MN=OM+ON \\
 & \Rightarrow MN=48+14=62cm \\
\end{align}\]
Now, applying the formula for area of trapezium given as: - Area = \[\dfrac{1}{2}\times \] (sum of parallel sides) \[\times \] height, we get,
\[\Rightarrow \] Area (ABCD) = \[\dfrac{1}{2}\times \left( AB+CD \right)\times MN\]
\[\Rightarrow \] Area (ABCD) = \[\dfrac{1}{2}\times \left( 96+28 \right)\times 62\]
\[\Rightarrow \] Area (ABCD) = \[\dfrac{1}{2}\times 124\times 62\]
\[\Rightarrow \] Area (ABCD) = 3844 \[c{{m}^{2}}\]

So, the correct answer is “Option c”.

Note: One may note that we have assumed the quadrilateral as a trapezium because we have been given that AB and CD are parallel to each other, that means only one pair of opposite sides were parallel. You must draw the diagram before solving the question so that all the conditions can easily get visualized. We have to look carefully in the diagram so that we can apply Pythagoras theorem properly.