
Two masses 7 kg and 12 kg are connected at the two ends of a light inextensible string over a frictionless pulley. Find the acceleration of the masses and the tension in the string, when the masses are released.

Answer
561.3k+ views
Hint: Since it is given that initially the entire system is at rest the first thing we should do is to balance the forces on every given block after releasing from the rest. When we balance all the forces we get the acceleration on each block and we will get the tension in the string connecting two blocks.
Complete step by step solution:
Same string is connecting the two blocks. Moreover it is given that the mass of string is negligible and there is no friction between string and pulley. So the tension in the string will be the same throughout. If no direction of motion of blocks nis given then we will assume one block is moving down and the other block is moving upwards.
Here it is given that the 12 kg block is moving downwards. So the 7kg block will move upwards.
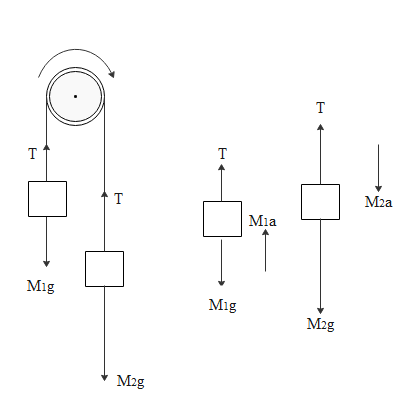
So from the above diagram if we write equations of motions for two blocks, we will get
$\eqalign{
& \Rightarrow {M_2}g - T = {M_2}a \cr
& \Rightarrow T - {M_1}g = {M_1}a \cr} $
By adding above two equations we will get acceleration as
$a = \dfrac{{\left( {{M_2} - {M_1}} \right)g}}{{{M_1} + {M_2}}}$
By substituting the acceleration equation in any of the above two equations we get tension as
$T = \dfrac{{2{M_1}{M_2}g}}{{{M_1} + {M_2}}}$
$ \Rightarrow a = \dfrac{{\left( {{M_2} - {M_1}} \right)g}}{{{M_1} + {M_2}}}$
$\eqalign{
& \Rightarrow a = \dfrac{{\left( {12 - 7} \right)10}}{{12 + 7}} \cr
& \therefore a = 2.631m/{s^2} \cr} $
Tension will be
$\eqalign{
& \Rightarrow T = \dfrac{{2{M_1}{M_2}g}}{{{M_1} + {M_2}}} \cr
& \Rightarrow T = \dfrac{{2\left( 7 \right)\left( {12} \right)10}}{{7 + 12}} \cr
& \therefore T = 88.42N \cr} $
Hence we had got the value of acceleration of blocks as 2.631 meter per second square and tension will be 88.42 newton.
Note: If there is friction between the pulley and the string and if pulley has certain mass then tensions in both the strings will be different and pulley will have angular acceleration and there will be torques produced by both the tensions and due to friction also. Ten we should consider the moment of inertia of pulley too to solve the problem.
Complete step by step solution:
Same string is connecting the two blocks. Moreover it is given that the mass of string is negligible and there is no friction between string and pulley. So the tension in the string will be the same throughout. If no direction of motion of blocks nis given then we will assume one block is moving down and the other block is moving upwards.
Here it is given that the 12 kg block is moving downwards. So the 7kg block will move upwards.

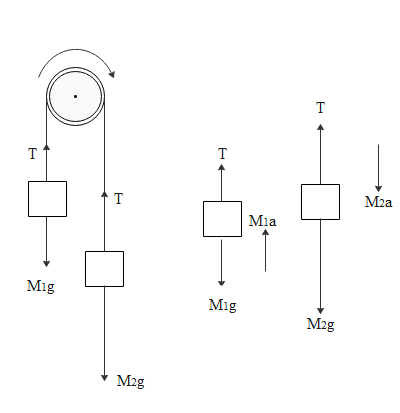
So from the above diagram if we write equations of motions for two blocks, we will get
$\eqalign{
& \Rightarrow {M_2}g - T = {M_2}a \cr
& \Rightarrow T - {M_1}g = {M_1}a \cr} $
By adding above two equations we will get acceleration as
$a = \dfrac{{\left( {{M_2} - {M_1}} \right)g}}{{{M_1} + {M_2}}}$
By substituting the acceleration equation in any of the above two equations we get tension as
$T = \dfrac{{2{M_1}{M_2}g}}{{{M_1} + {M_2}}}$
$ \Rightarrow a = \dfrac{{\left( {{M_2} - {M_1}} \right)g}}{{{M_1} + {M_2}}}$
$\eqalign{
& \Rightarrow a = \dfrac{{\left( {12 - 7} \right)10}}{{12 + 7}} \cr
& \therefore a = 2.631m/{s^2} \cr} $
Tension will be
$\eqalign{
& \Rightarrow T = \dfrac{{2{M_1}{M_2}g}}{{{M_1} + {M_2}}} \cr
& \Rightarrow T = \dfrac{{2\left( 7 \right)\left( {12} \right)10}}{{7 + 12}} \cr
& \therefore T = 88.42N \cr} $
Hence we had got the value of acceleration of blocks as 2.631 meter per second square and tension will be 88.42 newton.
Note: If there is friction between the pulley and the string and if pulley has certain mass then tensions in both the strings will be different and pulley will have angular acceleration and there will be torques produced by both the tensions and due to friction also. Ten we should consider the moment of inertia of pulley too to solve the problem.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Why is steel more elastic than rubber class 11 physics CBSE

What is boron A Nonmetal B Metal C Metalloid D All class 11 chemistry CBSE

Bond order ofO2 O2+ O2 and O22 is in order A O2 langle class 11 chemistry CBSE

Discuss the various forms of bacteria class 11 biology CBSE

What is the difference between biodegradable and nonbiodegradable class 11 biology CBSE




