Question

Two conducting spheres A and B of the same size are situated at some distance apart. Each has a charge of $ + q $ coulomb and they repel each other with a force of $ {10^{ - 5}}\,N $ . A third conducting uncharged sphere C of the same size is first touched with A and then with B and then placed exactly between A and B. Calculate the resultant force on C.

Answer 1

Hint: When two conducting spheres are touched, they distribute the sum of their charge equally with each other. The force on the third sphere will be calculated based on its charge and its distance from the other spheres from the coulomb’s law.

Formula used: In this solution, we will use the following formula:
Coulomb’s law: The force $ F $ between two charges Q and q: $ F = \dfrac{{kQq}}{{{r^2}}} $ where $ r $ is the distance between these two charges .

Complete step by step answer
We’ve been given that two conducting spheres have a charge $ + q $ and the force between them is $ {10^{ - 5}}\,N $ . If the distance between them is $ r $ , we can write from Coulomb’s law
 $ {10^{ - 5}} = \dfrac{{k{q^2}}}{{{r^2}}} $
Now when the third sphere of the same size is touched with the first sphere, the charge on both the spheres will be half of the net charge of the spheres. Since the net charge of sphere A and uncharged sphere C is $ 0 + q = q $ , when they’re touched, the charges on both of them will become
 $ {q_A} = {q_C} = \dfrac{q}{2} $ .

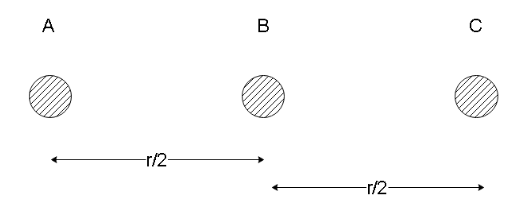
Now when the sphere C is touched with sphere B, the net charge between them is $ \dfrac{q}{2} + q = \dfrac{{3q}}{2} $ . This charge is equally split between both the charges so we have
 $ {q_C} = {q_B} = \dfrac{{3q}}{4} $
We know that sphere C is placed between A and B so its distance from the two charges will be $ r/2 $ . Hence the force on it will be due to both the other spheres will be opposing since other since all the charges are positive so, the net force will be
 $ F = \dfrac{{k(q)\left( {\dfrac{{3q}}{4}} \right)}}{{{{\left( {r/2} \right)}^2}}} - \dfrac{{k\left( {\dfrac{{3q}}{4}} \right)\left( {\dfrac{{3q}}{4}} \right)}}{{{{(r/2)}^2}}} $
This can be simplified as
 $ F = \dfrac{3}{2}\dfrac{{k{q^2}}}{{{r^2}}} - \dfrac{9}{4}\dfrac{{k{q^2}}}{{{r^2}}} $
Which gives us
 $ F = - \dfrac{3}{4}\dfrac{{k{q^2}}}{{{r^2}}} $
Since $ {10^{ - 5}} = \dfrac{{k{q^2}}}{{{r^2}}} $ , we have the force as
 $ F = - \dfrac{3}{4} \times {10^{ - 5}} $
 $ \therefore F = - 7.5 \times {10^{ - 6}}N $
The negative sign of the force indicates that the net force will be towards the direction of ball A.

Note
We don’t need to know the distance between A and B or its charge in terms of magnitude since as we saw, we can calculate the force in terms of the variables themselves. The assumption that the spheres have the same sizes is very important since it directly implies that the charge will be split such that both the spheres get half of the net charge. If their sizes were different, the charges would split depending on the radius of the spheres.