Question

Two charges $q$ and $ - 4q$ are kept in a straight line. At how many points on this line, the electric potential is zero?
A. $1$
B. $2$
C. $3$
D. Infinite

Answer 1

Hint: In order to solve this question we need to understand what electric potential is. Electric potential or potential difference is the amount of work done in moving a unit positive test charge from infinite to a point against the electric field with negligible acceleration so as to avoid energy lost due to radiation in motion. It is a scalar quantity, mathematically electrostatic potential directly proportional to the amount of test charge and inversely proportional to distance between the point and test charge.

Complete step by step answer:
Consider a charge $q$ at origin then the electrostatic potential due to this charge at point A which is at distance $r$ from charge is given by,
$V = \dfrac{{kq}}{r}$
Whereas “k” is proportionality constant and it is equal to $k = \dfrac{1}{{4\pi {\varepsilon _0}}}$. Here ${\varepsilon _0}$ is permittivity of free space and is equal to $8.854 \times {10^{ - 12}}{C^2}{N^{ - 1}}{m^{ - 2}}$

Let us consider charges situated on the x axis. So let us consider that charge $q$ is at origin and charge $ - 4q$ is at distance $d$ from charge $q$ having coordinate $(d,0)$.So let us take a point P at a distance x from q having coordinate as $(x,0)$.

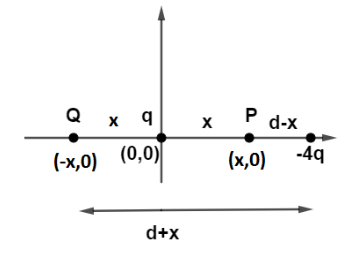
So electrostatic potential at P due to $q$ is given by ${V_1} = \dfrac{{kq}}{x}$.
Similarly, electrostatic potential at P due to $ - 4q$ is given by ${V_2} = \dfrac{{ - 4kq}}{{(d - x)}}$.
So net potential is $V = {V_1} + {V_2}$.
$V = kq(\dfrac{1}{x} - \dfrac{4}{{d - x}})$
So this potential is zero as $V = 0$
$kq\left( {\dfrac{1}{x} - \dfrac{4}{{d - x}}} \right) = 0$
$\Rightarrow \dfrac{{(d - x) - 4x}}{{x(d - x)}} = 0$
Equating the numerator to be zero we have
$d - 5x = 0$ Or $x = \dfrac{d}{5}$
So at $x = \dfrac{d}{5}$ electrostatic potential is zero

Now consider point Q at a distance x from q having coordinate as $( - x,0)$.
So electrostatic potential at Q due to $q$ is given by ${V_1} = \dfrac{{kq}}{x}$.
Similarly, electrostatic potential at Q due to $ - 4q$ is given by ${V_2} = \dfrac{{ - 4kq}}{{(d + x)}}$
So net potential is $V = {V_1} + {V_2}$
$V = kq(\dfrac{1}{x} - \dfrac{4}{{d + x}})$
So this potential is zero as $V = 0$
$kq\left( {\dfrac{1}{x} - \dfrac{4}{{d + x}}} \right) = 0$
$\Rightarrow \dfrac{{(d + x) - 4x}}{{x(d + x)}} = 0$
Equating the numerator to be zero we have
$d - 3x = 0$ Or $x = \dfrac{d}{3}$
So at $x = \dfrac{d}{3}$ electrostatic potential is zero

So the correct answer is A.

Note: It should be remembered that from multiple expansion of electrostatic potential it is clear that monopole is not zero so monopole contribution in electrostatic potential dominates compared to dipole and Quadrupole. If the monopole is zero then only the dipole contribution is necessary and also we can choose origin according to our own convenience.