Question

Two charges of equal magnitude $Q$ are placed at a separation $2a$ perpendicular to X- axis. Another charge, $q$ of mass $m$, is placed midway between the two charges on the X−axis. If this charges is displaced from equilibrium state to a distance $x(x < < a)$, then the particle
A. will execute simple harmonic motion about equilibrium position
B. will be oscillating about equilibrium position but not executes simple harmonic motion
C. will not return back to the equilibrium position
D. will stop at equilibrium position

Answer 1

Hint:We can find the nature of the motion of the charge particle by using the concept of necessary conditions to execute simple harmonic motion , Coulomb’s law of and the nature of charge particles.

Formula used:
Electrostatic force between two charges $Q$ & $q$ is given by
$F = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Qq}}{{{r^2}}}$
Where, ${\varepsilon _0}$ - permittivity of vacuum and $r$ - distance between the two charges.

Complete step by step answer:
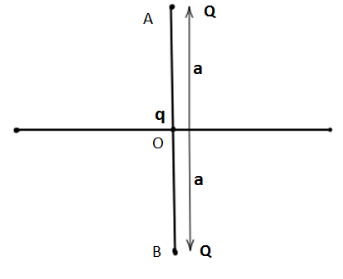
Let us consider two charges of equal magnitude $q$placed at a separation $2a$ perpendicular to the X- axis. Introducing another charge of magnitude $q$midway between the two charges on X – axis. Both the charges at A and B are of the same nature i.e. positive charges. If we place a positive charge midway between these two charges at O on the X-axis, then the particle at O exerts the same force on both end particles A and B.

But, when the particle at O is displaced slightly (say $x$) from its original position then the electrostatic force between the two charges charges, as

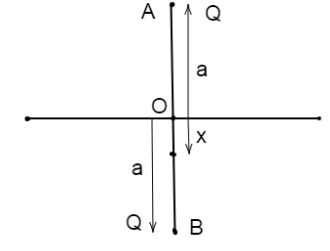
${F_1} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Qq}}{{{{(a + x)}^2}}}$ and ${F_2} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Qq}}{{{{(a - x)}^2}}}$
$\Rightarrow {F_2} - {F_1} = \dfrac{{Qq}}{{4\pi {\varepsilon _0}}}\left( {\dfrac{1}{{{{(a - x)}^2}}} - \dfrac{1}{{{{(a + x)}^2}}}} \right)$
Solving we get,
$\Rightarrow {F_2} - {F_1} = \dfrac{{Qq}}{{4\pi {\varepsilon _0}}}\left( {\dfrac{{4ax}}{{{{({a^2} - {x^2})}^2}}}} \right)$
$\therefore {F_1} - {F_2} = - \left( {\dfrac{{Qq}}{{{a^3}\pi {\varepsilon _0}}}} \right)x$
We get , $\therefore \left( {{F_1} - {F_2}} \right)\alpha - x$
Hence, By the definition of simple harmonic motion, we can say that the particle $q$ executes simple harmonic motion about equilibrium position.

Hence, the correct answer is option A.

Note:We must know the concept of simple harmonic motion that restoring force acting on the particle should always be proportional to the displacement of the particle and towards the equilibrium position. Also, make the diagram and place charged particles properly as given in question.