Question

Trace the straight line whose equation is $x + 2y + 3 = 0$

Answer 1

Hint: In this question you graph the given equation, so you can graph it by either intercept method or plotting-points method. In the intercept method you have to just find intercepts of abscissa and ordinate that is $x\;{\text{and}}\;y$ and then plot the graph. And in plotting-points method you have to find coordinates of the points in which the graph will lie, you can find them by putting random values of one of the variables in the equation and get the value of another one, then plot all points and the graph.

Complete step-by-step answer:
We will trace/graph the given equation $x + 2y + 3 = 0$ with help of intercept method,
So we will find $x\;{\text{and}}\;y$ intercepts
First finding $y$ intercept by putting the value of $x = 0$ in the equation, we will get
$
   \Rightarrow 0 + 2y + 3 = 0 \\
   \Rightarrow 2y = - 3 \\
   \Rightarrow y = - \dfrac{3}{2} \;
 $
Now finding $x$ intercept by putting the value of $y = 0$ in the equation, we will get
$
   \Rightarrow x + 2 \times 0 + 3 = 0 \\
   \Rightarrow x + 0 + 3 = 0 \\
   \Rightarrow x = - 3 \;
 $
Therefore the coordinates of $x\;{\text{and}}\;y$ intercepts will be written as $\left( { - 3,\;0} \right)\;{\text{and}}\;\left( {0,\; - \dfrac{3}{2}} \right)$ respectively.
Plotting the intercept points on a graph paper and then joining and extending the joined line in order to get the required trace or path or graph of the given equation, we will get

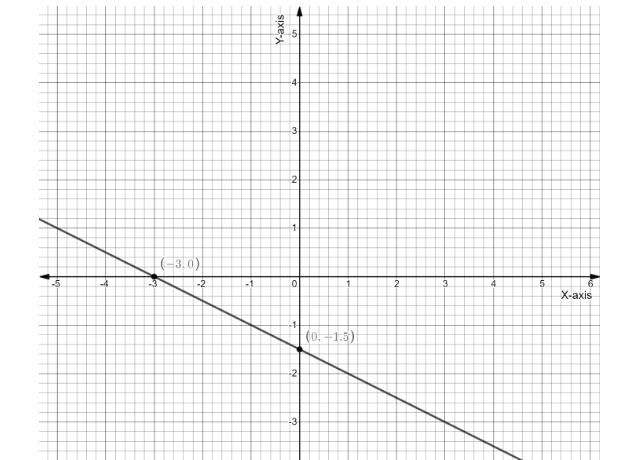
This is the required trace of the given equation.

Note: Plotting a graph with help of intercept method is only useful when the graph of the equation is not passing through the origin that is it must have $x\;{\text{and}}\;y$ intercepts, in other words, the equation should have a constant in it, if an equation does not contains constant then it means it is passing through the origin and its general equation can be written as $y = mx$