Question

Through a point P (h, k, l) a plane is drawn at right angles to OP to meet the coordinate axes in A, B and C. If OP = p, ${A_{xy}}$ is the area of projection of triangle ABC on XY–plane, ${A_{yz}}$ is area of projection of triangle ABC on YZ–plane, then
$\left( a \right)\Delta = \left| {\dfrac{{{p^5}}}{{hkl}}} \right|$
$\left( b \right)\Delta = \left| {\dfrac{{{p^5}}}{{2hkl}}} \right|$
$\left( c \right)\dfrac{{{A_{xy}}}}{{{A_{yz}}}} = \left| {\dfrac{l}{h}} \right|$
$\left( d \right)\dfrac{{{A_{xy}}}}{{{A_{yz}}}} = \left| {\dfrac{h}{l}} \right|$

Answer 1

Hint: In this particular question use the concept of direction ratios to find the equation of plane which is normal to OP which is given as, ax + by + cz = d, where a, b and c are the direction ratios of line OP and d is the distance of OP, so use these concept to reach the solution of the question.

Complete step-by-step answer:

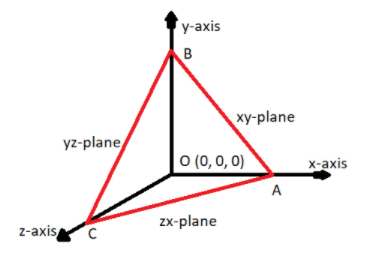
Given data:
A point P (h, k, l) a plane is drawn at right angles to OP to meet the coordinate axes in A, B and C.
It is also given that OP = p.
Where O is the origin (0, 0, 0)
So the distance of point P from the origin is given as,
$ \Rightarrow OP = \sqrt {{{\left( {h - 0} \right)}^2} + {{\left( {k - 0} \right)}^2}{{\left( {l - 0} \right)}^2}} = \sqrt {{h^2} + {k^2} + {l^2}} $
$ \Rightarrow p = \sqrt {{h^2} + {k^2} + {l^2}} $
$ \Rightarrow {p^2} = {h^2} + {k^2} + {l^2}$.................... (1)
Now the direction ratios of line OP is given as
$\left( {\dfrac{h}{p},\dfrac{k}{p},\dfrac{l}{p}} \right)$
Now since OP is normal to the plane so the equation of plane is given as,
$ \Rightarrow \dfrac{h}{p}x + \dfrac{k}{p}y + \dfrac{l}{p}z = p$
$ \Rightarrow hx + ky + lz = {p^2}$
Now as we know that the coordinates of triangle ABC lie on coordinates axis,
So for the coordinates of A substitute y = z = 0,
So the coordinate of A is $\left( {\dfrac{{{p^2}}}{h},0,0} \right)$
Similarly coordinates of B and C are $\left( {0,\dfrac{{{p^2}}}{k},0} \right)$ and $\left( {0,0,\dfrac{{{p^2}}}{l}} \right)$ respectively.
Therefore, A = $\left( {\dfrac{{{p^2}}}{h},0,0} \right)$, B = $\left( {0,\dfrac{{{p^2}}}{k},0} \right)$, and C = $\left( {0,0,\dfrac{{{p^2}}}{l}} \right)$
Now the area of triangle ABC is given as,
$ \Rightarrow \Delta = \sqrt {A_{xy}^2 + A_{yz}^2 + A_{zx}^2} $.................... (2)
Where, ${A_{xy}}$ is the area of projection of triangle ABC on XY–plane, ${A_{yz}}$ is area of projection of triangle ABC on YZ–plane and ${A_{zx}}$ is the area of projection of triangle ABC on ZX–plane.
Now as we know that the area of the triangle in 2-D passing from the points $\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right){\text{ and }}\left( {{x_3},{y_3}} \right)$ is half times the determinant of the vertices of the triangle so we have,
So the area of the triangle AOB is,
Where A = $\left( {\dfrac{{{p^2}}}{h},0,0} \right)$, B = $\left( {0,\dfrac{{{p^2}}}{k},0} \right)$, and O = (0, 0, 0)
$ \Rightarrow {A_{xy}} = \dfrac{1}{2}\left| {\begin{array}{*{20}{c}}
  {{x_1}}&{{y_1}}&1 \\
  {{x_2}}&{{y_2}}&1 \\
  {{x_3}}&{{y_3}}&1
\end{array}} \right| = \dfrac{1}{2}\left| {\begin{array}{*{20}{c}}
  {\dfrac{{{p^2}}}{h}}&0&1 \\
  0&{\dfrac{{{p^2}}}{k}}&1 \\
  0&0&1
\end{array}} \right|$
Now expand this determinant we have,

$ \Rightarrow {A_{xy}} = \dfrac{1}{2}\left| {\begin{array}{*{20}{c}}
  {\dfrac{{{p^2}}}{h}}&0&1 \\
  0&{\dfrac{{{p^2}}}{k}}&1 \\
  0&0&1
\end{array}} \right| = \dfrac{1}{2}\left| {\dfrac{{{p^2}}}{h}\left( {\dfrac{{{P^2}}}{k} - 0} \right) - 0 + 1\left( {0 - 0} \right)} \right|$
$ \Rightarrow {A_{xy}} = \dfrac{1}{2}\left| {\dfrac{{{p^4}}}{{hk}}} \right|$
Similarly, ${A_{yz}} = \dfrac{1}{2}\left| {\dfrac{{{p^4}}}{{kl}}} \right|$ and ${A_{zx}} = \dfrac{1}{2}\left| {\dfrac{{{p^4}}}{{lh}}} \right|$
Now from equation (2) we have,
$ \Rightarrow \Delta = \sqrt {\dfrac{1}{{{2^2}}}{{\left| {\dfrac{{{p^4}}}{{hk}}} \right|}^2} + \dfrac{1}{{{2^2}}}{{\left| {\dfrac{{{p^4}}}{{kl}}} \right|}^2} + \dfrac{1}{{{2^2}}}{{\left| {\dfrac{{{p^4}}}{{lh}}} \right|}^2}} $
$ \Rightarrow \Delta = \dfrac{{{p^4}}}{2}\sqrt {{{\left| {\dfrac{1}{{hk}}} \right|}^2} + {{\left| {\dfrac{1}{{kl}}} \right|}^2} + {{\left| {\dfrac{1}{{lh}}} \right|}^2}} $
$ \Rightarrow \Delta = \dfrac{{{p^4}}}{2}\sqrt {\left| {\dfrac{{{l^2} + {h^2} + {k^2}}}{{{h^2}\,{k^2}{l^2}}}} \right|} $
$ \Rightarrow \Delta = \dfrac{{{p^4}}}{{2hkl}}\sqrt {\left| {{l^2} + {h^2} + {k^2}} \right|} $
Now from equation 1 we have,
$ \Rightarrow \Delta = \dfrac{{{p^4}}}{{2hkl}}\sqrt {\left| {{p^2}} \right|} $
$ \Rightarrow \Delta = \dfrac{{{p^5}}}{{2hkl}}$
And the ratio of $\dfrac{{{A_{xy}}}}{{{A_{yz}}}}$ is
$ \Rightarrow \dfrac{{{A_{xy}}}}{{{A_{yz}}}} = \dfrac{{\dfrac{1}{2}\left| {\dfrac{{{p^4}}}{{hk}}} \right|}}{{\dfrac{1}{2}\left| {\dfrac{{{p^4}}}{{kl}}} \right|}} = \left| {\dfrac{l}{h}} \right|$
Hence options (b) and (c) are the correct answer.

Note: Whenever we face such types of questions the key concept we have to remember is that always recall that the area of the triangle in 2-D passing from the points $\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right){\text{ and }}\left( {{x_3},{y_3}} \right)$ is half times the determinant of the vertices of the triangle, i.e. $\dfrac{1}{2}\left| {\begin{array}{*{20}{c}}
  {{x_1}}&{{y_1}}&1 \\
  {{x_2}}&{{y_2}}&1 \\
  {{x_3}}&{{y_3}}&1
\end{array}} \right|$.