Question

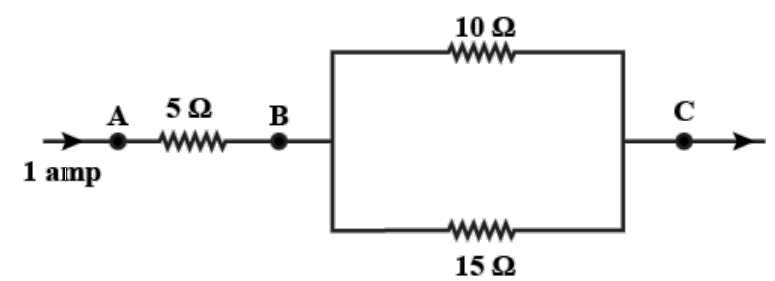
Three resistors are connected as shown in the diagram.
Through the resistor 5 ohm, a current of 1 ampere is flowing.
(i) What is the current through the other two resistors?
(ii) What is the potential difference across AB and AC?
(iii) What is the total resistance?

Answer 1

Hint – In order to solve this problem we need to find the potential difference between B and C then we can get the current. Then we have to apply the rules for connection series and parallel to get the equivalent resistance.
Formula used – V=IR, Total resistance in series = sum of all the resistances in series.

Complete Step-by-Step solution:
The current from A to B and B to C is 1 amp.
The resistors of 10 and 15 ohms are in parallel then the potential difference will be the same in both resistors.
The resistance between B and C will be $\dfrac{{10{\text{x15}}}}{{10\, + \,15}} = \dfrac{{150}}{{25}} = 6\Omega $.
Then the voltage between the resistor of 6 ohm and current of 1 amp is V=IR.
V=1(6)=6V
Therefore the potential difference is 6 volts in 10 and 15 ohm resistors.
(i)Then the current between 10 and 15 ohm resistor is,
${I_{10}} = \dfrac{{{V_{10}}}}{{10}} = \dfrac{6}{{10}} = 0.6A$
And ${I_{15}} = \dfrac{{{V_{15}}}}{{15}} = \dfrac{6}{{15}} = 0.4A$
(ii) Potential difference between AB is
${V_{AB}} = {I_{AB}}{R_{AB}} = 1{\text{ x 5 = 5V}}$
${V_{BC}} = {I_{BC}}{R_{BC}} = 1{\text{ x 6 = 6V}}$
So, ${V_{AC}} = {V_{AB}} + {V_{BC}} = 5 + 6 = 11$
Hence, the potential difference is 11 volts between AC and 5 volts between AB.
(iii) The equivalent resistance between A and C can be calculated as:
As the resistance between B and C is 6 ohm as calculated above.
And the resistance between A and B is 5 ohm we can clearly see they both are in series since the current passing through then is 1 ampere.
So, when the resistance is in series they add up to give the total effective resistance. So, ${R_{AC}} = 6 + 5 = 11\Omega $.

Note – To solve these types of problems we need to know the ohms law that is potential difference is directly proportional to resistance V=IR and we also need to know that in series the resistance adds up to give the effective resistance that it is larger than the largest resistance. Also the voltage in parallel resistances or any other elements connected in parallel are the same. Knowing this will solve your problem.