Question

Three dimensions of cuboid are \[3\] cm, \[4\] cm and \[5\] cm. Draw an isometric sketch of this cuboid and hence find the volume of the cuboid.
(A) \[20c{m^3}\]
(B) \[60c{m^3}\]
(C) \[64c{m^3}\]
(D) \[125c{m^3}\]

Answer 1

Hint: In this question, we have the three dimensions of cuboid.
We need to first draw an isometric sketch of this cuboid and hence find out the volume of the cuboid.
 We will calculate the volume using the formula and given in particular.

Formula used: The volume of cuboid, $V = lbh = l \times b \times h$
Where,
l = Length of the cuboid
b = breadth of the cuboid
h = Height of the cuboid

Complete step-by-step solution:
It is given that three dimensions of the cuboid are \[3\] cm, \[4\] cm and \[5\] cm.
We need to first draw an isometric sketch of this cuboid and hence find out the volume of the cuboid.
An isometric drawing is a type of \[3D\] drawing that is set out using \[30\]-degree angles. It's a type of axonometric drawing in which the same scale is used for every axis, resulting in a non-distorted image.

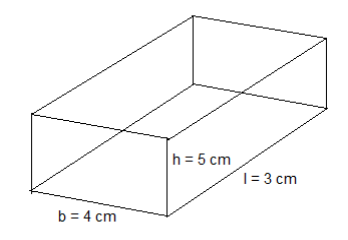
Here,
l = Length of the cuboid = \[3\] cm
b = breadth of the cuboid = \[4\] cm
h = Height of the cuboid = \[5\] cm
Using the formula of the volume of cuboid we have,
The volume of cuboid, $V = lbh = l \times b \times h$
\[ \Rightarrow 3 \times 4 \times 5c{m^3}\]
\[ \Rightarrow 60c{m^3}\]
$\therefore $ Option (B) is the correct option.

Note: We can observe that Isometric Sketching or isometric drawing is a pictorial representation of an object in which all the three-dimensions are drawn at the full scale. It looks like an isometric projection. In this case, all the lines parallel to its major axes are measurable.