Question

Three charges 2q, −q, −q are located at the vertices of an equilateral triangle. At the centre of the triangle:
A. The field is zero but the potential is non – zero
B. The field is non – zero but the potential is zero
C. Both field and potential are zero
D. Both field and potential are non – zero

Answer 1

Hint: We are given an equilateral triangle and 2 charges placed at its vertices. We need to find the electric field and potential at the centre of the triangle. We know that for an equilateral triangle the distance from all vertices to centre will be the same. By using the respective equations, we can find the field and potential.
Formula used:
$E=\dfrac{KQ}{{{r}^{2}}}$
$U=\dfrac{kQ}{{{r}^{2}}}$

Complete answer:
In the question it is said that 3 charges 2q, -q and –q are placed at the three vertices of an equilateral triangle.
We are asked to determine the electric field and the potential at the centre of the triangle.
Consider the figure given below.

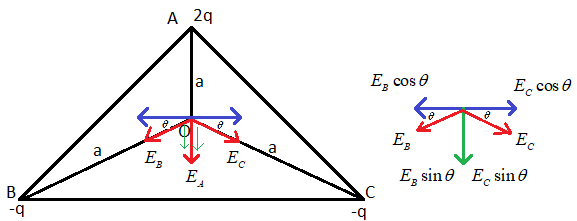
It shows the electric field at the centre of the equilateral triangle.
The charge 2q is placed at ‘A’, -q at ‘B’ and –q at C. ‘O’ is the centre of the triangle and ‘a’ is the distance from the vertices to the centre.
‘${{E}_{A}}$’ is the electric field experienced at the centre of the triangle due to the charge placed at ‘A’. Since the charge at ‘A’, 2q is positive; the direction of the electric field will be away from the charge.
‘${{E}_{B}}$’ is the electric field experienced at the centre of the triangle. Since the charge at ‘B’, -q is a negative charge, the direction of the electric field will be toward the charge.
‘${{E}_{C}}$’ is the electric field at ‘O’ due to the charge at ‘C’. Since –q is negative, the direction of ‘${{E}_{C}}$’ will be towards the charge.
The charge at ‘B’ and ‘C’ is –q.
We know that the electric field is given by the equation,
$E=\dfrac{KQ}{{{r}^{2}}}$, where ‘K’ is a constant, ‘Q’ is the charge and ‘r’ is the distance between the reference point and charge.
Therefore the field at ‘O’ due to ‘B’ will be,
${{E}_{B}}=\dfrac{K\left( -q \right)}{{{a}^{2}}}$
And the charge at ‘O’ due to ‘C’ will be,
${{E}_{C}}=\dfrac{K\left( -q \right)}{{{a}^{2}}}$
From this we can see that, ${{E}_{B}}={{E}_{C}}$
The components of ‘${{E}_{B}}$’ and ‘${{E}_{C}}$’ are resolved as ${{E}_{B}}\sin \theta ,{{E}_{B}}\cos \theta $ and ${{E}_{C}}\sin \theta ,{{E}_{C}}\cos \theta $ respectively.
From the figure we can see that ${{E}_{B}}\cos \theta $ and ${{E}_{C}}\cos \theta $ are equal and opposite. Hence they get cancelled.
Therefore the remaining components of are ${{E}_{B}}\sin \theta $ and ${{E}_{C}}\sin \theta $.
Therefore the net electric field experienced at the centre of the triangle,
$E={{E}_{A}}+{{E}_{B}}\sin \theta +{{E}_{C}}\sin \theta $
Thus we can see that the electric field at the centre of the triangle is non – zero.
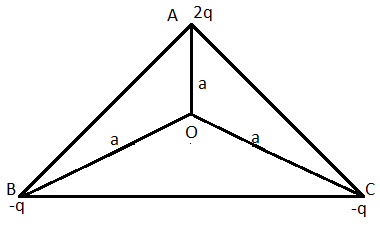
Now let us find the electric potential at the centre of the triangle. For that consider the figure given below.

We know that the electric potential is given by the equation,
$U=\dfrac{kQ}{{{r}^{2}}}$, where ‘K’ is a constant, ‘Q’ is the charge and ‘r’ is the distance from the charge to the point.
Here let $'{{U}_{A}}','{{U}_{B}}'$ and $'{{U}_{C}}'$ be the electric potential at centre due to ‘A’, ‘B’ and ‘C’ respectively. Then we have,
${{U}_{A}}=\dfrac{k\left( 2q \right)}{{{a}^{2}}}$
${{U}_{B}}=\dfrac{k\left( -q \right)}{{{a}^{2}}}$
${{U}_{C}}=\dfrac{k\left( -q \right)}{{{a}^{2}}}$
Therefore the net electric potential at the centre will be,
\[U={{U}_{A}}+{{U}_{B}}+{{U}_{C}}\]
$\Rightarrow U=\dfrac{k\left( 2q \right)}{{{a}^{2}}}+\dfrac{k\left( -q \right)}{{{a}^{2}}}+\dfrac{k\left( -q \right)}{{{a}^{2}}}$
$\Rightarrow U=\dfrac{k\left( 2q \right)}{{{a}^{2}}}-\dfrac{k\left( 2q \right)}{{{a}^{2}}}$
$\Rightarrow U=0$
Thus we get the electric potential at the centre as zero.
Therefore we have the electric field at the centre of the triangle as non – zero and the electric potential at the centre of the triangle as zero.

So, the correct answer is “Option B”.

Note:
Electric field is a vector quantity, i.e. a quantity with both magnitude and direction. It is simply defined as the force per unit charge at point.
Mathematically we can write,
$E=\dfrac{F}{{{q}_{0}}}$, were ‘F’ is the force and ‘${{q}_{0}}$’ is the test charge.
From coulomb’s law we have the equation for force as,
$F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q{{q}_{0}}}{{{r}^{2}}}$, were ‘q’ is the charge, ‘${{q}_{0}}$’ is the test charge and ‘r’ is the distance between them.
Therefore we get the electric field as,
$E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{{{r}^{2}}}$