Question

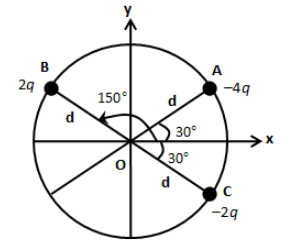
Three charged particles A, B and C with charges \[ - 4q\], \[2q\] and \[ - 2q\] are present on the circumference of a circle of radius d. The charged particles A, C and centre O of the circle formed an equilateral triangle as shown in the figure. Electric field at O along x-direction is:

Answer 1

Hint: The imaginary test charge at point O, will be attracted by charges A and C and repelled by charge B. So, the direction of the electric field at point O due to charges \[ - 4q\]and \[ - 2q\] is towards A and C respectively. Also, the electric field at point o due to charge \[2q\] is towards point C. Calculate the x-component of the electric field at point O by taking the addition of electric fields due to each charge.

Formula used:
Electric field, \[E = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{{{d^2}}}\],
where, \[{\varepsilon _0}\] is the permittivity of free space, q is the charge and d is the distance.

Complete step by step answer:
We know the like charges repel each other while unlike charges attract towards each other. Therefore, the imaginary test charge at point O, will be attracted by charges A and C and repelled by charge B. So, the direction of the electric field at point O due to charges \[ - 4q\]and \[ - 2q\] is towards A and C respectively. Also, the electric field at point o due to charge \[2q\] is towards point C as shown in the figure below.

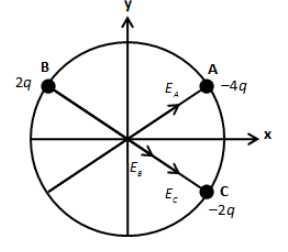
Let us express the magnitude of electric field at point O due to charge \[ - 4q\] as follows,
\[{E_A} = k\dfrac{{ - 4q}}{{{d^2}}}\] …… (1)
Here, k is the constant and it has value \[k = \dfrac{1}{{4\pi {\varepsilon _0}}}\], where, \[{\varepsilon _0}\] is the permittivity of the free space.

Let us express the magnitude of electric field at point O due to charge \[2q\] as follows,
\[{E_B} = k\dfrac{{2q}}{{{d^2}}}\] …… (2)
Let us express the magnitude of electric field at point O due to charge \[ - 2q\] as follows,
\[{E_C} = k\dfrac{{ - 2q}}{{{d^2}}}\] …… (3)
The direction of the electric field at point O along the horizontal direction x is can be expressed as,
\[{E_x} = {E_A}\cos 30^\circ + {E_B}\cos 30^\circ + {E_C}\cos 30^\circ \]
\[ \Rightarrow {E_x} = \left( {{E_A} + {E_B} + {E_C}} \right)\cos 30^\circ \]
\[ \Rightarrow {E_x} = \left( {{E_A} + {E_B} + {E_C}} \right)\dfrac{{\sqrt 3 }}{2}\]
Using equation (1), (2) and (3) in the above equation, we get,
\[{E_x} = \left( {k\dfrac{{ - 4q}}{{{d^2}}} + k\dfrac{{2q}}{{{d^2}}} + k\dfrac{{ - 2q}}{{{d^2}}}} \right)\dfrac{{\sqrt 3 }}{2}\]
\[ \Rightarrow {E_x} = k\dfrac{q}{{{d^2}}}\left( { - 4 + 2 + - 2} \right)\dfrac{{\sqrt 3 }}{2}\]
\[ \therefore {E_x} = - 2\sqrt 3 \,k\dfrac{q}{{{d^2}}}\]

This is the expression for the horizontal component of the electric field at point O.

Note:The crucial step in the solution is to determine the direction of the electric field due to the given charges. If the charge at B is negative, then the direction of the electric field would be towards the charge. The x-component of this electric field would be along the negative x-axis. Note that \[\cos \left( { - \theta } \right) = \cos \theta \].