Question

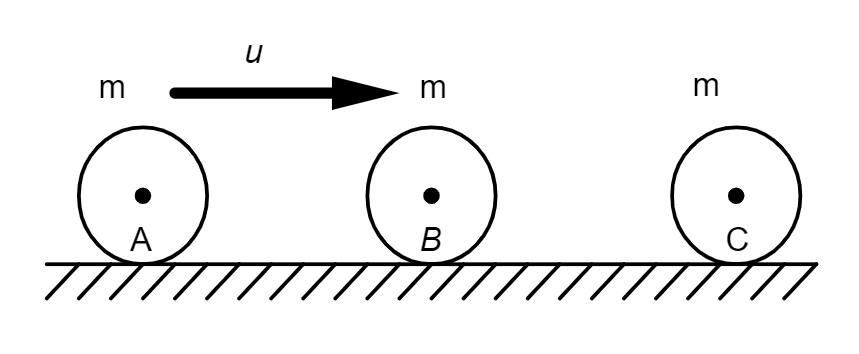
Three balls, A, B, C of the same mass $m$ are placed on a frictionless horizontal plane in a straight line as shown in the figure. Ball A is moved with velocity $u$ towards the middle ball B. If all the collisions are elastic, find the final velocities of all the balls.

Answer 1

Hint: During elastic collisions, kinetic energies are conserved. The sum of kinetic energies before collision is equal to the sum of final kinetic energies. An object moving with a particular velocity before collision stops after transferring the kinetic energy to the other object. The second object starts moving with the same velocity and energy with which it was hit. Momentums of the objects are also conserved during elastic collisions.

Formula used: Kinetic energy $K.E =\dfrac { 1 }{ 2 } mv^{ 2 }$ where $m$ is the mass and $v$ is the velocity of the object.

Complete step by step answer:
From the figure, it is clear that a total number of two collisions are happening on a whole. In the first collision, the first ball A hits the second ball B with a velocity $u$ and in the second collision, the second ball B hits the third ball B with an unknown velocity. This unknown velocity is nothing but the final velocity of the second ball after the first collision. We are required to calculate the final velocities of all the three balls after every collision.
First of all, let us assign variables to the required data as mentioned below:
$m$ - mass of each ball
$u$ - initial velocity of ball A
$v$ - final velocity of ball A
$w$ - initial velocity of ball B
$x$ - final velocity of ball B
$y$ - initial velocity of ball C
$z$ - final velocity of ball C
We are required to calculate $v$, $x$ and $z$ from the information provided.
Now, let us consider the case of the first collision. Ball A hits ball B with a velocity of $u$. It is said that the collision is elastic. For elastic collisions, kinetic energies are conserved. The sum of kinetic energies before collision is equal to the sum of final kinetic energies. So, we have the relation:
$\dfrac { 1 }{ 2 } m{ u }^{ 2 }\quad +\quad \dfrac { 1 }{ 2 } m{ w }^{ 2 }\quad =\quad \dfrac { 1 }{ 2 } m{ v }^{ 2 }\quad +\quad \dfrac { 1 }{ 2 } m{ x }^{ 2 }$
Here,
 $u$ – initial velocity of the ball A = $u$ (given)
$v$ – final velocity of ball A = 0 (ball A stops after transferring the whole energy to ball B due to elastic collision)
$w$ – initial velocity of ball B = 0 (at rest on a horizontal frictionless surface)
$x$ – final velocity of ball B
Simplifying the above equation, we have
$\dfrac { 1 }{ 2 } m{ u }^{ 2 }\quad +\quad \dfrac { 1 }{ 2 } m{ (0) }^{ 2 }\quad =\quad \dfrac { 1 }{ 2 } m{ (0) }^{ 2 }\quad +\quad \dfrac { 1 }{ 2 } m{ x }^{ 2 }$
$\dfrac { 1 }{ 2 } m{ u }^{ 2 }\quad =\quad \dfrac { 1 }{ 2 } m{ x }^{ 2 }$
${ u }^{ 2 }\quad =\quad { x }^{ 2\quad }\Rightarrow \quad u\quad =\quad x$ (Equation 1)
Therefore, after the first collision, the final velocity of ball B is nothing but the initial velocity of ball A.
Now, let us move on to the second collision. Ball B hits ball C. Again, it is said that the collision is elastic. For elastic collisions, kinetic energies are conserved. The sum of kinetic energies before collision is equal to the sum of kinetic energies after collision. So, we have the relation:
$\dfrac { 1 }{ 2 } mw^{ 2 }\quad +\quad \dfrac { 1 }{ 2 } m{ y }^{ 2 }\quad =\quad \dfrac { 1 }{ 2 } m{ x }^{ 2 }\quad +\quad \dfrac { 1 }{ 2 } m{ z }^{ 2 }$
Here,
$w$ – initial velocity of the ball B = $x$ (The final velocity of ball B in the first collision is equal to the initial velocity of ball B in the second collision)
$x$ – final velocity of ball B = 0 (ball B stops after transferring the whole energy to ball C due to elastic collision)
$y$ – initial velocity of ball C = 0 (at rest on a horizontal frictionless surface)
$z$ – final velocity of ball C

On simplification,
$\dfrac { 1 }{ 2 } mx^{ 2 }\quad +\quad \dfrac { 1 }{ 2 } m(0)^{ 2 }\quad =\quad \dfrac { 1 }{ 2 } m{ (0) }^{ 2 }\quad +\quad \dfrac { 1 }{ 2 } m{ z }^{ 2 }$
$\dfrac { 1 }{ 2 } m{ x }^{ 2 }\quad =\quad \dfrac { 1 }{ 2 } m{ z }^{ 2 }$
$x^{ 2 }\quad =\quad z^{ 2\quad }\Rightarrow \quad x\quad =\quad z\quad \Rightarrow \quad x\quad =\quad z\quad =\quad u$ (from equation 1)
To sum up, after both the collisions, the final velocities of ball A, ball B and ball C ($v$, $x$ and $z$) are $0$, $0$ and $u$ respectively.

Note: Students should not get confused with the initial and final velocities of first collision and second collision. The use of different variables for each data can solve the problem.
The concept can also be explained using the principle of conservation of momentum. In this case, the equation turns out to be ${{m}_{1}}{{v}_{1}}={{m}_{2}}{{v}_{2}}$ for each set of collision. Students need to remember the formula of kinetic energy or that of momentum to solve the question easily.