Question

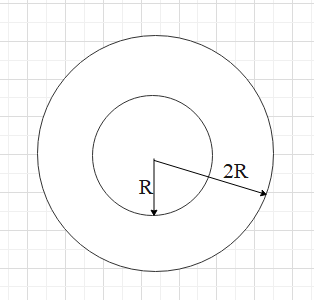
There is a concentric hole of radius R in a solid sphere of radius 2R. Mass of the remaining portion is M. What is the gravitational potential at the centre?

A. \[\dfrac{-5GM}{7R}\]
B. \[\dfrac{-7GM}{14R}\]
C. \[\dfrac{-3GM}{7R}\]
D. \[\dfrac{-9GM}{14R}\]

Answer 1

Hint: Formula for gravitational potential have been used. We will consider a circle of the same radius as that of the cavity with negative mass that can fill the sphere. After calculating the potential for both spheres we will get the gravitational potential at center.

Formula used:
Mass = Volume $\times$ Density
\[v=\dfrac{-3GM}{2R}\]

Complete step by step answer:
We have a sphere shell with inner radius R and outer radius 2R. The leftover mass between the two circles is M. We have to calculate the gravitational potential at the center.
For any solid sphere the potential at the center is given by
\[v=\dfrac{-3GM}{2R}\]
As we have to find potential and there is a cavity in the center. Let us assume that we fill the cavity with a sphere having negative mass that can fill the sphere. Let us calculate the density be and we know formula of solid sphere will be
\[\begin{align}
  & \dfrac{4}{3}\pi {{r}^{3}}=\dfrac{4}{3}\pi \left[ {{(2R)}^{3}}-{{R}^{3}} \right] \\
 & \dfrac{4}{3}\pi (7{{R}^{3}})\rho =M \\
\end{align}\]
The mass for sphere with radius 2R
\[\dfrac{4}{3}\pi (8{{R}^{3}})\rho =\dfrac{8}{7}M\]
Therefore the mass of the left over sphere will be \[\dfrac{M}{7}\] and mass will be negative because we have assumed a negative mass.
So the potential for both the sphere
\[\begin{align}
  & -\dfrac{3}{2}G\left[ \dfrac{{}^{8M}/{}_{7}}{2R}-\dfrac{{}^{M}/{}_{7}}{R} \right]=-\dfrac{3}{2}G\left[ \dfrac{4M}{7R}-\dfrac{M}{7R} \right] \\
 & =\dfrac{-9GM}{14R} \\
\end{align}\]
Thus gravitational potential at center is \[\dfrac{-9GM}{14R}\] . So option D is correct.

Note:
The term gravitational potential arises from the law of gravity. It can be considered as the work done to bring a mass to a given point against gravity. For some questions the value for gravitational potential is used directly, as we used the gravitational potential at the center. So it should be remembered.