Question

The sun subtends an angle of \[{\left( {\dfrac{1}{2}} \right)^o}\]at the surface of the earth. A converging lens of focal length 100 cm is used to obtain an image of sun on a screen. The diameter of the image formed is about:
A) 1 mm
B) 9 mm
C) 18 mm
D) 50 mm

Answer 1

Hint: As the sun is at infinite distance, we can draw the ray diagram of its light falling from infinity into the converging (convex) lens and forming an image of the screen. Using this diagram we can calculate the required diameter of the image.

Formula used:
${\theta _{rad}} = \dfrac{l}{r}$ where ${\theta _{rad}}$ is the measure of angle in radians, l is the length of the arc and r is the radius.

Complete step by step answer:
Converging lens means convex lens. The sun can be considered to be at infinite distance from the earth and if the ray of light comes from infinity into the convex lens, the image is always formed at the focus at focal length of the lens. This is because the screen will be placed on the focal point.
The ray diagram for a sunlight falling on a convex lens is given as:

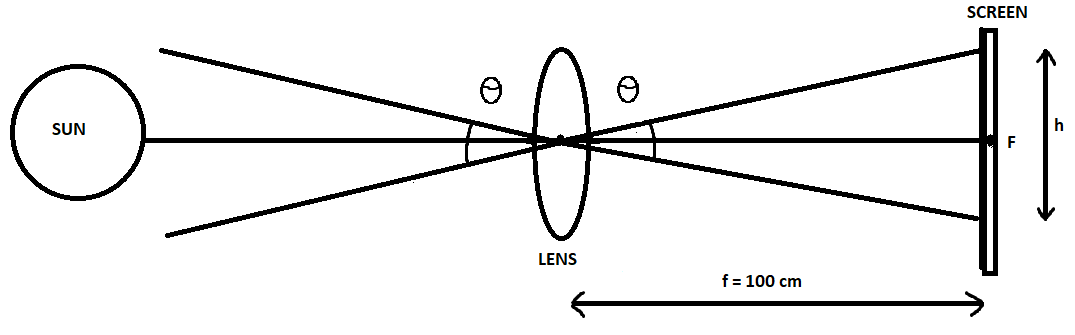
The angle subtended by the rays is $\theta $ and the angle formed opposite to it is also $\theta $ as they are vertically opposite. The diameter of the image is represented by h and the given focal length (f) of the lens is 100 cm.
The given value of $\theta $ is \[{\left( {\dfrac{1}{2}} \right)^o}\].
When the angle is in radians, it is equal to the length of arc per unit radius. Mathematically:
${\theta _{rad}} = \dfrac{l}{r}$ and here:
Length of arc (l) = diameter of the image formed (h)
Radius (r) = focal length (f)
$ \Rightarrow {\theta _{rad}} = \dfrac{h}{f}$
Given value of angle is in degrees and in radians it can be written as:
${\left( {\dfrac{1}{2}} \right)^o} = \left( {\dfrac{\pi }{{180}} \times \dfrac{1}{2}} \right)rad$
f = 100 cm (given)
Substituting the values and calculating diameter of the image formed:
$
  \left( {\dfrac{\pi }{{180}} \times \dfrac{1}{2}} \right) = \dfrac{h}{{100}} \\
\implies h = 100 \times \left( {\dfrac{\pi }{{180}} \times \dfrac{1}{2}} \right) \\
\implies h = 100 \times \dfrac{\pi }{{360}} \\
\implies h = 100 \times \dfrac{{3.14}}{{360}}\left( {\because \pi = 3.14} \right) \\
\therefore h = 0.87 \\
 $
As the given focal length is in cm, this diameter will also be in cm but the given options are in mm, so:
0.87 cm = 8.7 mm (As 10 mm = 1 cm)
$8.7mm \approx 9mm$.
Therefore, the diameter of the image formed is about 9 mm.

So, the correct answer is “Option B”.

Note:
Lens is made up of two spherical surfaces and if these are bent outwards, it is called a convex lens and it is thicker at the centre.
The rays that pass through the convex lens are converged at one point and thus it is also known as a converging lens.
Remember that $\pi $ radians is equal to 180° and 1cm is equal to 100 mm.