Question

The sum of the interior angles of a pentagon is _____________.

Answer 1

Hint: We here have been asked about the sum of the interior angles of a triangle. For finding that, let us first know about a pentagon:
A pentagon is any five-sided polygon. Since it has 5 sides, its name has a prefix ‘pent’ and hence known as pentagon. A regular pentagon is shown as follows:

Now, to find the sum of all interior angles of a pentagon, we will use the formula \[A=\left( n-2 \right)\times {{180}^{\circ }}\] where ‘A’ is the sum of interior angles of a polygon with ‘n’ sides.

Complete step-by-step answer:
Now, we have to find the sum of the interior angles of a pentagon.
We know that the sum of interior angles ‘A’ of any polygon of sides ‘n’ is given by the formula \[A=\left( n-2 \right)\times {{180}^{\circ }}\]. Thus, we will use this formula to find the required sum.
We know that a pentagon has 5 sides. Thus, $n=5$.
Putting the value of ‘n’ in the formula, we get:
\[\begin{align}
  & A=\left( n-2 \right)\times {{180}^{\circ }} \\
 & \Rightarrow A=\left( 5-2 \right)\times {{180}^{\circ }} \\
 & \Rightarrow A=3\times {{180}^{\circ }} \\
\end{align}\]
\[\Rightarrow A={{540}^{\circ }}\]
Thus, the sum of interior angles of a pentagon is ${{540}^{\circ }}$.
Now, let us find out the measure of each angle in a regular pentagon.
We can find it through the following method:
We will divide the sum of the measures of the angles by the number of sides of the polygon.
Sum of the measure of the angles of a pentagon=${{540}^{\circ }}$
No. of sides in a pentagon= 5
Thus, measure of one angle of a regular pentagon is give as:
 $\begin{align}
  & \dfrac{{{540}^{\circ }}}{5} \\
 & \Rightarrow {{108}^{\circ }} \\
\end{align}$
Therefore, the measure of one angle of a regular pentagon is 108°.

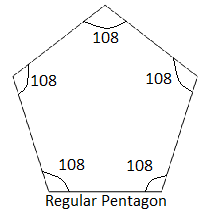
We can verify it by multiplying 108° by 5.
\[108{}^\circ \times 5=540{}^\circ \]
But this can only be calculated if the polygon is regular, i.e. we can only find the measure of one angle of a pentagon if the pentagon is a regular one, i.e., all of its sides are of the equal length.
Thus, the required answer is ${{540}^{\circ }}$.

Note: We must know the sum of the interior angles of the basic polygons as they can come in handy.
1. TRIANGLE: The sum of the interior angles of a triangle is always 180°.
2. QUADRILATERAL: The sum of the interior angles of a quadrilateral is always 360°.
3. PENATGON: The sum of the interior angles of a pentagon is always 540°.