Question

The sum of the exterior angles of a hexagon is:
(A) ${360}^{\circ }$
(B) ${540}^{\circ }$
(C) ${720}^{\circ }$
(D) None of these

Answer 1

Hint: Hexagon is a polygon having six sides. Sum of its interior angles is ${720}^{\circ }$. But the sum of exterior angles of any polygons is ${360}^{\circ }$ irrespective of the number of sides in the polygon.

Complete step-by-step answer:

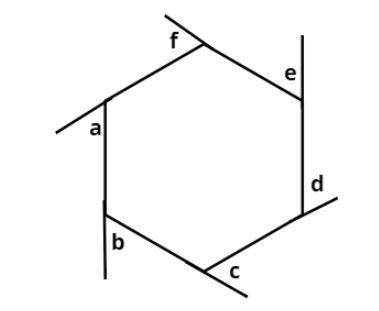
A hexagon is a polygon consisting of six sides. The total of the internal angles of a hexagon is ${720}^{\circ }$.
If the hexagon is a regular hexagon, all the six sides of it are equal and all the six internal angles are also equal. And the measure of each angle is ${120}^{\circ }$.
While the sum of interior angles of a polygon varies with the number of sides in a polygon, the sum of exterior angles remains the same for all polygons and it is ${360}^{\circ }$.
In our case, if the hexagon is a regular hexagon, all the six exterior angles will be equal and each of them will measure ${60}^{\circ }$. But if it is not regular, their values will differ. But the sum will always be the same which is ${360}^{\circ }$.
Therefore, in the figure:
$\Rightarrow a+b+c+d+e+f={360}^{\circ }$

(A) is the correct option.

Note: Sum of the interior angles of a polygon is determined by the formula $\left(n-2\right)\times {180}^{\circ }$ where $n$ is the number of sides in the polygon. And the sum of exterior angles is ${360}^{\circ }$ irrespective of the number of sides in the polygon.