Question

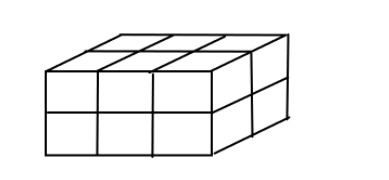
The solid brick shown is made of small bricks of side $ 1 $ . When the large brick is disassembled into its component small bricks, the total surface area of all the small bricks is how much greater than the surface area of the larger brick?

Answer 1

Hint: In order to find the difference between the surface area of the small and the larger brick, first find the surface area of the smaller brick using its side. Then find the surface area of the larger brick in which the length, breadth and height are changed as small cubic bricks are added to make a cuboid brick.

Complete step-by-step answer:
We are given a larger brick, which is made up of joining small bricks of side $ 1 $ unit.
The diagram of small bricks is:

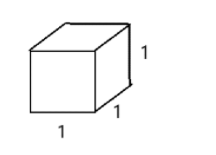
Since, nothing else is given except its side, so it’s a cubic brick.
From the mensuration formula for the surface area of the cube, we know that the surface area of the cube $ = 6{a^2} $ , where $ a = $ length of the side.
So, for our question $ a = 1 $ unit.
Substituting the value of $ a $ in the surface area formula and we get:
Surface area of one cubic/small brick $ = 6{a^2} = 6{\left( 1 \right)^2} = 6 $ sq. unit
From the figure, we can see that there are $ 6 $ small bricks at front side, and there are $ 6 $ bricks back side that means there are $ 12 $ small bricks in total.
The Surface area of all the $ 12 $ Smaller bricks is the surface area of one brick multiplied by $ 12 $ bricks.
Therefore, The Surface area of all the smaller bricks is $ 12 \times 6 = 72 $ sq. unit ……(1)
But, the larger brick is made up of this kind of smaller brick, and forms a cuboid.
From the figure given above we can see that there are $ 3 $ bricks joined in length. So, the length becomes $ 1 + 1 + 1 = 3 $ unit.
There are two layers of bricks one above another, so the height becomes $ 1 + 1 = 2 $ unit.
Similarly, there are two layers in the bottom, so breath becomes $ 1 + 1 = 2 $ unit.
Therefore, the dimensions of the larger brick is:
Length $ \left( l \right) = 3 $ unit
Breadth $ \left( b \right) = 2 $ unit
Height $ \left( h \right) = 2 $ unit
The new diagram for larger brick is :

From the mensuration formula for surface area of cuboid, we know that the surface area of cuboid $ = 2\left( {lb + bh + lh} \right) $ , where $ l = length $ , $ b = breadth $ and $ h = height $ .
Substituting the value of $ l,b,h $ in the surface area formula and we get:
 $
  SA = 2\left( {lb + bh + lh} \right) \\
  SA = 2\left( {3 \times 2 + 2 \times 2 + 3 \times 2} \right) \;
  $
Solving the parenthesis and, we get:
 $
  SA = 2\left( {3 \times 2 + 2 \times 2 + 3 \times 2} \right) \\
  SA = 2\left( {6 + 4 + 6} \right) \\
  SA = 2\left( {16} \right) \\
  SA = 32 \;
  $
Therefore, surface area of one large brick $ = 32 $ sq. unit ……………(2)
Subtracting (2) from (1):
 $ 72 - 32 = 40 $ sq. unit.
Therefore, the total Surface area of small bricks is $ 40 $ sq. unit greater than the large brick.

Note: Do not commit a mistake to take the same length, breadth and height for the cuboid. The dimensions are changed when small bricks are added to form a large brick.
There are twelve small bricks in total, so don’t forget to multiply the surface area of one brick with twelve in order to find the total surface area of the small brick.