Question

The resistance and inductance of the series circuit are$5\Omega $ and 20H respectively. At the instant of closing the switch, the current is increasing at the rate 4A/s. The supply voltage is
A. 20V
B. 80V
C. 120V
D. 100V

Answer 1

Hint: You could derive the expression for instantaneous current in LR circuit using kirchhoff's voltage rule. Then, if you differentiate the same with respect to time, you get the required equation for solving the question. Also, take t=0 at the instant of closing the switch.

Formula used:
Kirchoff’s voltage law,
$V=i\times R+L\dfrac{di}{dt}$
Expression for current in LR circuit,
${{i}_{\left( t \right)}}=\dfrac{V}{R}\left( 1-{{e}^{-\dfrac{Rt}{L}}} \right)$

Complete step by step answer:
In this question we are given a circuit with the resistor and inductor connected in series, that is a series L-R circuit,

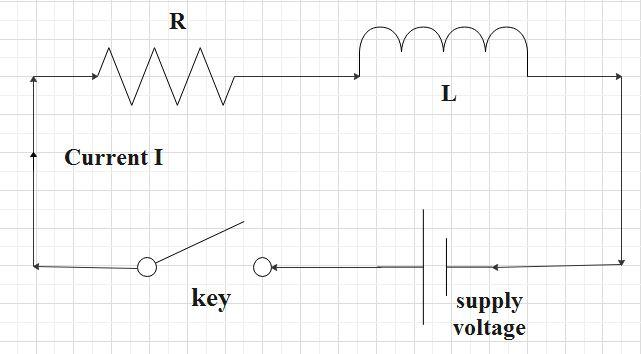
From Kirchoff’s voltage law, we have that the sum of changes in potential in any closed loop involving resistors and cells is zero. Therefore,
$V={{V}_{R}}+{{V}_{L}}$ ……………… (1)
Where, $V\to $ Supply voltage
${{V}_{R}}$ = voltage drop across the resistor
${{V}_{L}}$ = voltage drop across the inductor
Also,
${{V}_{R}}=i\times R$ ……………….. (2)
${{V}_{L}}=L\dfrac{di}{dt}$ ……………….. (3)
Substituting (2) and (3) in (1), we get,
$V=i\times R+L\dfrac{di}{dt}$ …………………. (4)
Clearly, the voltage drop across the resistor depends on the current ‘i’ and that of the inductor is dependent on the rate of change of current $\left( \dfrac{di}{dt} \right)$. By rearranging equation (4) and applying integration, we get,
$\int\limits_{0}^{t}{\dfrac{dt}{L}}=\int\limits_{0}^{i}{\dfrac{di}{V-iR}}$ ……………. (5)
Let us integrate the RHS using substitution method,
Let,
$V-iR=z$…………… (6)
Then,
$\dfrac{dz}{di}=-R$
$di=\dfrac{dz}{-R}$ ……………… (7)
Substituting (6) and (7) in (5),
$\int\limits_{0}^{t}{\dfrac{dt}{L}}=-\dfrac{1}{R}\int{\dfrac{dz}{z}}$
LHS= $\dfrac{1}{L}\left[ t \right]_{0}^{t}=\dfrac{t}{L}$ ……………. (8)
We know that, $\int{\dfrac{dz}{z}}=\ln (z)$
We could now substitute for z from (6)
RHS= $-\dfrac{1}{R}\ln \left( V-iR \right)_{0}^{i}$
By applying limits and$\ln (a)-\ln (b)=\ln \left( \dfrac{a}{b} \right)$, we get,
RHS= $-\dfrac{1}{R}\left( \ln \left( V-iR \right)-\ln (V) \right)=-\dfrac{1}{R}\ln \dfrac{V-iR}{V}$ ……………….. (9)
Now equating LHS and RHS from (8) and (9) gives,
$\dfrac{-Rt}{L}=\ln \dfrac{V-iR}{V}$
Now let us take antilog on both sides,
${{e}^{-\dfrac{Rt}{L}}}=\dfrac{V-iR}{V}$
By rearranging the above equation, we get the expression for the current in LR series circuit as,
${{i}_{\left( t \right)}}=\dfrac{V}{R}\left( 1-{{e}^{-\dfrac{Rt}{L}}} \right)$ …………… (10)
In the question we are given the rate of increase of current in the circuit at the instant the switch is closed, that is, let t=0 be the time at which the switch is closed, rate of increase of electric current at that instant is,
$\dfrac{di}{dt}=4A{{s}^{-1}}$
Let us represent the peak value of current in the circuit as, ${{i}_{0}}=\dfrac{V}{R}$
Now equation (10) could be written as,
${{i}_{\left( t \right)}}={{i}_{0}}\left( 1-{{e}^{-\dfrac{Rt}{L}}} \right)$ ……………. (11)
Differentiating (11) with respect to t gives,
$\dfrac{di}{dt}=-{{i}_{0}}\left( -\dfrac{R}{L}{{e}^{-\dfrac{Rt}{L}}} \right)$
$\dfrac{di}{dt}=\dfrac{V}{L}\left( {{e}^{-\dfrac{Rt}{L}}} \right)$ ……………….. (12)
At the instant when the switch is on, (t=0), the exponential term in (12) becomes,
${{e}^{-\dfrac{R\times 0}{L}}}={{e}^{0}}=1$
So (12) now becomes,
$\dfrac{di}{dt}=\dfrac{V}{L}$ ……………. (13)
Now, all we have to do is to substitute the given values in the question to equation (13).
We have,
$\dfrac{di}{dt}=4A{{s}^{-1}}$
$L=20H$
Therefore, the supply voltage in the given circuit V is,
$V=\dfrac{di}{dt}\times L$
$V=4\times 20=80V$
Hence, we get the answer to the question as option B.

Note:
We should remember that we are dealing with LR circuits and hence the instantaneous current has a dependency on time. If you knew the expression for the instantaneous current, we could have saved time by avoiding the derivation of this expression from Kirchoff’s law. Also, note that we are given the rate of increase in current $\left( \dfrac{di}{dt} \right)$ not the current (i) itself.