Question

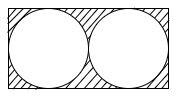
The ratio of total area of the rectangle to the total shaded area is

A. $\dfrac{2}{\pi }$
B. $\dfrac{4}{4-\pi }$
C. $\dfrac{4-\pi }{\pi }$
D. $\dfrac{\pi }{4}$

Answer 1

Hint: In order to solve this question, we should know that the area of a rectangle is given by $l\times b$, where l is the length and b is the breadth and that the area of a circle is given by $\pi {{r}^{2}}$, where r is the radius. So, we will first find the radius of the circle and the length and breadth of the rectangle and then we will be able to get the answer.

Complete step-by-step answer:
In this question, we have been asked to find the ratio of the total area of the rectangle to the shaded region in the given figure below.

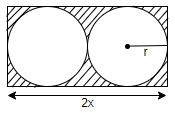
To solve this question, we will start by considering the length of the rectangle as 2x, as shown in the above figure. Now, from the figure we can see that both the circles are touching 3 sides of the rectangle and the other circle on the fourth side. So, we can say that both the circles are of equal radius and the sum of the diameter of both the circles is equal to the length of the rectangle. So, we can say that if radius of the circle is r, then,
$\begin{align}
  & 2r+2r=2x \\
 & \Rightarrow 4r=2x \\
 & \Rightarrow r=\dfrac{x}{2} \\
\end{align}$
Hence, we can say that the radius of the circle is x and the radius is $\dfrac{x}{2}$. Now, we know that the breadth of the rectangle is equal to the diameter of the circle. So, we can say that the breadth of the rectangle is x. We know that the total area of the rectangle is calculated by the formula $l\times b$. So, we get the area of the rectangle as $2x\times x=2{{x}^{2}}$.
Now, we know that the area of the shaded region can be calculated by subtracting the area covered by both the circles from the area of the rectangle. So, we get area of shaded region as,
Area of rectangle - area of both the circles.
Now, we know that the area of the circle is given by $\pi {{r}^{2}}$ and for radius = $\dfrac{x}{2}$, we get the area of the circle as $\pi \dfrac{{{x}^{2}}}{4}$. Therefore, we can write the area of the shaded region for area of rectangle, $2{{x}^{2}}$ as,
$\begin{align}
  & 2{{x}^{2}}-2\pi \dfrac{{{x}^{2}}}{4} \\
 & \Rightarrow {{x}^{2}}\left( 2-\dfrac{\pi }{2} \right) \\
\end{align}$
Now, we are asked to find the ratio of the total area of the rectangle to the area of the shaded region. So, we get,
$\text{Ratio=}\dfrac{\text{Area of rectangle}}{\text{Area of shaded region}}$
And we can further write it as,
$\begin{align}
  & \text{Ratio=}\dfrac{2{{x}^{2}}}{{{x}^{2}}\left( 2-\dfrac{\pi }{2} \right)} \\
 & \Rightarrow \text{Ratio=}\dfrac{2}{2-\dfrac{\pi }{2}} \\
 & \Rightarrow \text{Ratio=}\dfrac{2}{\dfrac{4-\pi }{2}} \\
 & \Rightarrow \text{Ratio=}\dfrac{4}{4-\pi } \\
\end{align}$
Hence, we can say that the ratio of the total area of the rectangle to the total shaded area as $\dfrac{4}{4-\pi }$.
Therefore, option B is the correct answer.
Note: The possible mistakes that we can make while solving this question is by calculating the wrong ratio, which could be ratio of rectangle to the ratio of circle or ratio of circle to the ratio of shaded region or something similar. This will lead to an incorrect answer, so one should be careful while taking the ratios.