
The potential difference across $ 8 $ ohm resistance is $ 48 $ volt as shown in the figure. The value of potential difference across X and Y points will be
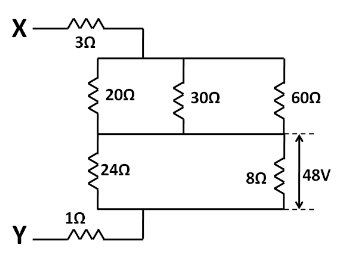
(A) $ 128 $ volt
(B) $ 160 $ volt
(C) $ 80 $ volt
(D) $ 62 $ volt

Answer
556.5k+ views
Hint : To solve this question, we need to assume a battery between the points X and Y of emf equal to the unknown potential difference. Then we have to simplify the circuit by calculating the parallel equivalent resistance.
Complete step by step answer
Let the potential difference across X and Y points be $ V $ . So let us consider a battery of emf $ V $ connected across the points X and Y as shown in the figure below.
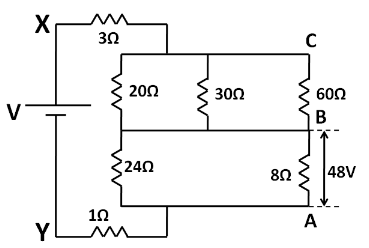
According to the question, the potential difference across the $ 8 $ ohm resistance is equal to $ 48 $ volt. So referring to the above figure, the potential difference between the points A and B is $ 48 $ volt. According to the polarity of the battery, the point B should be at a higher potential than the point A. So we have
$\Rightarrow {V_{BA}} = 8{\text{V}} $ ……………………….(1)
Now, the $ 24\Omega $ and $ 8\Omega $ resistances are in parallel combination across the point A and B. So the equivalent resistance between the points A and B, $ {R_{AB}} $ is given by
$\Rightarrow \dfrac{1}{{{R_{AB}}}} = \dfrac{1}{8} + \dfrac{1}{{24}} $
On solving we get
$\Rightarrow {R_{AB}} = 6\Omega $
Also, across the points B and C, the $ 20\Omega ,30\Omega ,60\Omega $ resistances are arranged in parallel combination. So the equivalent resistance across the points B and C is given by
$\Rightarrow \dfrac{1}{{{R_{BC}}}} = \dfrac{1}{{20}} + \dfrac{1}{{30}} + \dfrac{1}{{60}} $
On solving we get
$\Rightarrow {R_{BC}} = 10\Omega $
So the above circuit can be redrawn as
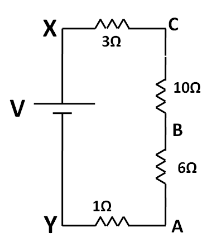
Now, let $ I $ be the current in the circuit. From Ohm’s law we have
$\Rightarrow V = IR $ ..........................(2)
Now, the equivalent resistance in the circuit is given by
$\Rightarrow R = 3\Omega + 10\Omega + 6\Omega + 1\Omega $
$ \Rightarrow R = 20\Omega $
So from (2) we have
$\Rightarrow V = 20I $
$ \Rightarrow I = \dfrac{V}{{20}} $ ........................(3)
The potential difference across the points A and B is equal to that across the $ 6\Omega $ resistance. Therefore we have
$\Rightarrow {V_{BA}} = 6I $
From (3)
$\Rightarrow {V_{BA}} = \dfrac{{6V}}{{20}} $ ........................(4)
Equating (1) and (4) we have
$\Rightarrow \dfrac{{6V}}{{20}} = 48 $
$ \Rightarrow V = 160{\text{V}} $
Thus, the potential difference between the points X and Y is equal to $ 160 $ volts.
Hence, the correct answer is option B.
Note
The points X and Y are not shown to be connected through any battery in the figure given in the question. But the potential difference which is given across the $ 8 $ ohm resistance clearly indicates that a voltage source must be present there. Hence we were able to assume the battery between X and Y.
Complete step by step answer
Let the potential difference across X and Y points be $ V $ . So let us consider a battery of emf $ V $ connected across the points X and Y as shown in the figure below.

According to the question, the potential difference across the $ 8 $ ohm resistance is equal to $ 48 $ volt. So referring to the above figure, the potential difference between the points A and B is $ 48 $ volt. According to the polarity of the battery, the point B should be at a higher potential than the point A. So we have
$\Rightarrow {V_{BA}} = 8{\text{V}} $ ……………………….(1)
Now, the $ 24\Omega $ and $ 8\Omega $ resistances are in parallel combination across the point A and B. So the equivalent resistance between the points A and B, $ {R_{AB}} $ is given by
$\Rightarrow \dfrac{1}{{{R_{AB}}}} = \dfrac{1}{8} + \dfrac{1}{{24}} $
On solving we get
$\Rightarrow {R_{AB}} = 6\Omega $
Also, across the points B and C, the $ 20\Omega ,30\Omega ,60\Omega $ resistances are arranged in parallel combination. So the equivalent resistance across the points B and C is given by
$\Rightarrow \dfrac{1}{{{R_{BC}}}} = \dfrac{1}{{20}} + \dfrac{1}{{30}} + \dfrac{1}{{60}} $
On solving we get
$\Rightarrow {R_{BC}} = 10\Omega $
So the above circuit can be redrawn as

Now, let $ I $ be the current in the circuit. From Ohm’s law we have
$\Rightarrow V = IR $ ..........................(2)
Now, the equivalent resistance in the circuit is given by
$\Rightarrow R = 3\Omega + 10\Omega + 6\Omega + 1\Omega $
$ \Rightarrow R = 20\Omega $
So from (2) we have
$\Rightarrow V = 20I $
$ \Rightarrow I = \dfrac{V}{{20}} $ ........................(3)
The potential difference across the points A and B is equal to that across the $ 6\Omega $ resistance. Therefore we have
$\Rightarrow {V_{BA}} = 6I $
From (3)
$\Rightarrow {V_{BA}} = \dfrac{{6V}}{{20}} $ ........................(4)
Equating (1) and (4) we have
$\Rightarrow \dfrac{{6V}}{{20}} = 48 $
$ \Rightarrow V = 160{\text{V}} $
Thus, the potential difference between the points X and Y is equal to $ 160 $ volts.
Hence, the correct answer is option B.
Note
The points X and Y are not shown to be connected through any battery in the figure given in the question. But the potential difference which is given across the $ 8 $ ohm resistance clearly indicates that a voltage source must be present there. Hence we were able to assume the battery between X and Y.
Recently Updated Pages
Describe the mechanism of absorption of water by r class 12 biology CBSE

The north and south poles of two identical magnets class 12 physics CBSE

Characteristic feature of mangrove plants is aApospory class 12 biology CBSE

Explain the composition of triglyceride class 12 biology CBSE

Convert i 3Methylaniline into 3nitrotoluene class 12 chemistry CBSE

Explain chemical effect of electric current with an class 12 physics CBSE

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

The pH of the pancreatic juice is A 64 B 86 C 120 D class 12 biology CBSE

Explain sex determination in humans with the help of class 12 biology CBSE




