Questions & Answers
Question
Answers
Related Questions
: The perimeter of an isosceles triangle is 90 m. If the length of the two equal sides is $\dfrac{3}{4}$ of the length of the unequal side, find the dimensions of the triangle.
Answer
![Verified]()
Verified
Verified
Hint: With the given perimeter ,we can form a linear equation with two variables and by solving it we get the dimensions of the triangle.
Complete step-by-step answer:
Step 1:
It is given that it is an isosceles triangle. In an isosceles triangle any two sides are equal .
We are given the perimeter of the triangle and we know that the perimeter of the triangle is just the sum of its three sides.
Step 2 :
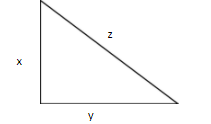
Let the length of the sides be x , y , z.
Perimeter = x+y+z
Since it is an isosceles triangle, x = y
Therefore , perimeter = x + x +z
$ \Rightarrow 90 = 2x + z$………….(1)
Step 3:
It is given that the length of the two equal sides is $\dfrac{3}{4}$ of the length of the unequal side.
$ \Rightarrow x = \dfrac{3}{4}z$
Cross multiplying we get
$
\Rightarrow 4x = 3z \\
\Rightarrow \dfrac{4}{3}x = z \\
$
Now lets substitute the above value in equation (1)
$ \Rightarrow 90 = 2x + \dfrac{4}{3}x$
Taking LCM , we get
$ \Rightarrow 90 = \dfrac{{6x + 4x}}{3}$
Cross multiplying we get,
$
\Rightarrow 270 = 10x \\
\Rightarrow \dfrac{{270}}{{10}} = x \\
\Rightarrow x = 27m \\
$
Now we have obtained the value of x and as it is an isosceles triangle y = 27 m
Step 4 :
To find the value of z , substitute the value of x in equation (1)
$
\Rightarrow 90 = 2(27) + z \\
\Rightarrow 90 = 54 + z \\
\Rightarrow 90 - 54 = z \\
\Rightarrow z = 36m \\
$
Therefore the value of z=36m
Therefore, the dimensions of the isosceles triangle are 27 m , 27 m , 36 m.
Note: In this problem we have used a substitution method to solve the linear equation but we can also use elimination method to solve them.
Complete step-by-step answer:
Step 1:
It is given that it is an isosceles triangle. In an isosceles triangle any two sides are equal .
We are given the perimeter of the triangle and we know that the perimeter of the triangle is just the sum of its three sides.
Step 2 :
Let the length of the sides be x , y , z.
Perimeter = x+y+z
Since it is an isosceles triangle, x = y
Therefore , perimeter = x + x +z
$ \Rightarrow 90 = 2x + z$………….(1)
Step 3:
It is given that the length of the two equal sides is $\dfrac{3}{4}$ of the length of the unequal side.
$ \Rightarrow x = \dfrac{3}{4}z$
Cross multiplying we get
$
\Rightarrow 4x = 3z \\
\Rightarrow \dfrac{4}{3}x = z \\
$
Now lets substitute the above value in equation (1)
$ \Rightarrow 90 = 2x + \dfrac{4}{3}x$
Taking LCM , we get
$ \Rightarrow 90 = \dfrac{{6x + 4x}}{3}$
Cross multiplying we get,
$
\Rightarrow 270 = 10x \\
\Rightarrow \dfrac{{270}}{{10}} = x \\
\Rightarrow x = 27m \\
$
Now we have obtained the value of x and as it is an isosceles triangle y = 27 m
Step 4 :
To find the value of z , substitute the value of x in equation (1)
$
\Rightarrow 90 = 2(27) + z \\
\Rightarrow 90 = 54 + z \\
\Rightarrow 90 - 54 = z \\
\Rightarrow z = 36m \\
$
Therefore the value of z=36m
Therefore, the dimensions of the isosceles triangle are 27 m , 27 m , 36 m.
Note: In this problem we have used a substitution method to solve the linear equation but we can also use elimination method to solve them.
×
Sorry!, This page is not available for now to bookmark.
Like this
Liked
-
LIVECourses
-
Crash Courses 2021
-
Vedantu Pro
-
Vedantu Assist
-
Class 12
-
-
JEE
-
JEE Main & Advanced 2021
-
JEE Main & Advanced 2022
-
-
NEET
-
NEET 2021
-
NEET 2022
-
-
NDA
-
CBSE
-
Commerce
-
Class 11
-
Class 12
-
-
ICSE
-
Maharashtra Board
-
Class 9
-
Class 10
-
-
Micro Courses
-
-
FREEMaster Classes
-
PREMIUM1-on-1 Classes
-
Study Material
-
NCERT Solutions
-
Previous Year Papers
-
Mock Tests
-
Sample Papers
-
Reference Book Solutions
-
ICSE Solutions
-
School Syllabus
-
Revision Notes
-
Important Questions
-
Math Formula Sheets
-
-
More
Book your FREE Online counselling session
Share your contact information
Your FREE Online counselling session has been booked!
Vedantu academic counsellor will be calling you shortly for your Online Counselling session.
DONE
Please try again later
OK
NCERT Book Solutions
Reference Book Solutions
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
(Mon-Sun: 9am - 11pm IST)
Questions?
Chat with us
