Question

The perimeter of a rhombus is 52 cm and one of its diagonals is 24 cm. The length of the other diagonal is
A) 24 cm
B) 10 cm
C) $2\dfrac{1}{6}cm$
D) 12 cm

Answer 1

Hint: As all the sides of a rhombus are equal in length and its perimeter is given, we can find the length of the sides. The diagonals of a rhombus are bisect each other at 90°, using this fact in the given length of the diagonal, we can find the unknown length of the other triangle.
Formula to be used:
Perimeter of rhombus = 4s , where s is its side
${\left( H \right)^2} = {\left( P \right)^2} + {\left( B \right)^2}$where H is the hypotenuse, P is the perpendicular and B is the base of the right angle.

Complete step by step solution:
The perimeter and a diagonal of the rhombus are given to be 52 cm and 24 cm respectively.
Perimeter of rhombus = 4s , where s is the length side as all the sides are equal in length.
$
  \therefore 4s = 52 \\
   \Rightarrow s = \dfrac{{52}}{4} \\
   \Rightarrow s = 13 \;
 $
The diagonals of a rhombus bisects each other at right angles i.e. 90°. So the figure of the rhombus is given as:

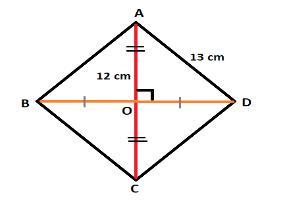
ABCD is a rhombus with side 13 cm and one of its diagonal equal to 24 cm but as these are bisected, the measure of half the diagonal becomes half the length i.e. 12 cm.
The length required to be calculated is that of the diagonal BD which is double of that of OD and can be written as:
$ \Rightarrow BD = 2OD....(1)$
Now, as the diagonals bisect at 90°, $\vartriangle AOD$ becomes a right angled triangle and we can apply Pythagoras theorem so as to calculate the value of OD.
Applying Pythagoras theorem on $\vartriangle AOD$:
${\left( H \right)^2} = {\left( P \right)^2} + {\left( B \right)^2}$
Here,
Hypotenuse (H) = AD = 13 cm
Perpendicular (P) = AO = 12 cm
Base (B) = OD
Substituting the values, we get:
$
  {\left( {13} \right)^2} = {\left( {12} \right)^2} + {\left( {OD} \right)^2} \\
   \Rightarrow {\left( {OD} \right)^2} = {\left( {13} \right)^2} - {\left( {12} \right)^2} \\
   \Rightarrow {\left( {OD} \right)^2} = 169 - 144 \\
   \Rightarrow {\left( {OD} \right)^2} = 25 \;
 $
Taking square root both the sides:
$
  \sqrt {{{\left( {OD} \right)}^2}} = \sqrt {25} \\
   \Rightarrow OD = 5{\text{ }}cm \\
 $
Substituting this value in (1) to get the length of the diagonal:
$
  BD = 2 \times 5{\text{ }}cm \\
   \Rightarrow BD = 10{\text{ }}cm \;
 $
Therefore, the length of the other diagonal of the given rhombus is 10 cm
So, the correct answer is “ 10 cm”.

Note: The term ‘bisect’ means dividing into equal parts, when the diagonals of the rhombus cut each other their respective lengths become half as they get bisected that too at right angles. Pythagora's theorem is applicable to only right angled triangles i.e. when an angle enclosed measures 90°. Hypotenuse is always the longest side of the triangle and the line on which the angle is formed is its base.