Question

The orbit of the planet Mercury around the Sun is in elliptical shape with the sun at a focus. The semi major axis is of length 36 million miles and the eccentricity of the orbit is 0.206. Find:
$\left( i \right)$ How close the mercury gets to the Sun?
$\left( {ii} \right)$ The greatest possible distance between Mercury and Sun.

Answer 1

Hint: In this particular types of question use the concept that in a ellipse the length of the major axis = 2a, and the length of the minor axis = 2b, (e) is the eccentricity and the coordinates of the focus is (ae, 0) and (-ae, 0) so use these concepts to reach the solution of the question.

Complete step by step solution:

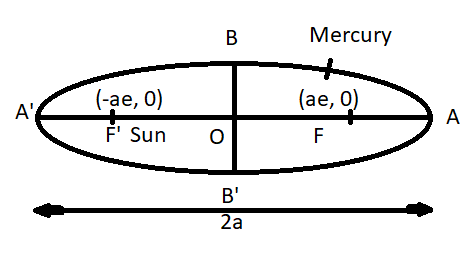
Description of the above diagram:
O is the center of the ellipse, AA’ is the semi major axis and BB’ is the semi minor axis and F and F’ are the focus of the ellipse.
The length of the major axis = 2a, and the length of the minor axis = 2b, (e) is the eccentricity as shown in the figure.
So length of semi major axis is = a, and length of semi minor axis = b
The coordinates of the focus is (ae, 0) and (-ae, 0) as shown in the figure.
Now the orbit of the planet Mercury is elliptical as shown in the figure, and the Sun is at one of the focus.
Let the Sun is at focus F’ as shown in the figure.
Now it is given that length of semi major axis is of length 36 million miles, and the eccentricity = 0.206
Therefore, a = 36 million miles and e = 0.206.
$\left( i \right)$ How close the mercury gets to the Sun?
Now from the figure it is clear that the closest distance of the mercury from the Sun is when Mercury is at point F’.
So the closest distance is F’A’.
Now as we all know that from origin the point (A) and (A’) are at equal distance so, OA = OA’ = (2a/2) = a.
And the distance of point F’ from the origin is ae.
Therefore, OF’ = ae.
So from the figure the distance A’F’ = OA’ – OF’
Now substitute the variables we have,
$ \Rightarrow A'F' = a - ae$
Now substitute the values we have,
$ \Rightarrow A'F' = 36\left( {1 - 0.206} \right)$
Now simplify this we have,
$ \Rightarrow A'F' = 36\left( {0.794} \right) = 28.584$ Million miles.
$\left( {ii} \right)$ The greatest possible distance between Mercury and Sun.
So from the figure it is clear that the greatest possible distance between Mercury and Sun is = F’A
Therefore from the figure, F’A = OA + OF’
Now substitute the variables we have,
$ \Rightarrow F'A = a + ae$
Now substitute the values we have,
\[ \Rightarrow F'A = 36\left( {1 + 0.206} \right)\]
Now simplify this we have,
$ \Rightarrow F'A = 36\left( {1.206} \right) = 43.416$ Million miles.
So this is the required answer.

Note: Whenever we face such types of questions the key concept we have to remember is that if one object is on one of the focus (say F’) of the ellipse and the other object is on the circumference of the ellipse then the greatest and smallest distance between these objects is the distance between the focus and the end points of the semi major axis.