Question

The number of students in a hostel, speaking different languages is given below.
Display the data in a pie chart.

Language	Hindi	English	Marathi	Tamil	Bengali	Total
Number of students	40	12	9	7	4	72

Answer 1

Hint: Here, we know that the total number of outcomes is 72 and use the formula of the probability of any event happening is given by dividing the number of outcomes of that event divided by the total number of events, that is; $P = \dfrac{{{\text{Number of outcomes}}}}{{{\text{Total number of outcomes}}}}$. Then we will use the given conditions to find the required probability and then we will convert the obtained probability in degrees of the pie chart by multiplying it by \[360^\circ \]. Then we will use these degrees to make the pie chart.

Complete step by step solution: We know that the total number of outcomes is 72.

First, we will take language Hindi from the given table.

We know that the probability of any event happening is given by dividing the number of outcomes of that event divided by the total number of events, that is; $P = \dfrac{{{\text{Number of outcomes}}}}{{{\text{Total number of outcomes}}}}$.

Substituting the values of the number of outcomes of speaking Hindi and the total number of outcomes in the above formula, we get
\[
   \Rightarrow {P_{Hindi}} = \dfrac{{40}}{{72}} \\
   \Rightarrow {P_{Hindi}} = \dfrac{5}{9} \\
 \]

Converting the above probability in degrees of the pie chart by multiplying it by \[360^\circ \], we get
\[
   \Rightarrow {P_{Hindi}} = \dfrac{5}{9} \times 360^\circ \\
   \Rightarrow {P_{Hindi}} = 200^\circ \\
 \]

We will now take language English from the given table.

We will use the formula of probability and substitute the values of the number of outcomes of speaking English and the total number of outcomes, we get
\[
   \Rightarrow {P_{English}} = \dfrac{{12}}{{72}} \\
   \Rightarrow {P_{English}} = \dfrac{1}{6} \\
 \]
Converting the above probability in degrees of the pie chart by multiplying it by \[360^\circ \], we get
\[
   \Rightarrow {P_{English}} = \dfrac{1}{6} \times 360^\circ \\
   \Rightarrow {P_{English}} = 60^\circ \\
 \]

Now, we will take language Marathi from the given table.

We will use the formula of probability and substitute the values of the number of outcomes of speaking Marathi and the total number of outcomes, we get
\[
   \Rightarrow {P_{Marathi}} = \dfrac{9}{{72}} \\
   \Rightarrow {P_{Marathi}} = \dfrac{1}{8} \\
 \]

Converting the above probability in degrees of the pie chart by multiplying it by \[360^\circ \], we get
\[
   \Rightarrow {P_{Marathi}} = \dfrac{1}{8} \times 360^\circ \\
   \Rightarrow {P_{Marathi}} = 45^\circ \\
 \]

We will take language Tamil from the given table.

We will use the formula of probability and substitute the values of the number of outcomes of speaking Tamil and the total number of outcomes, we get
\[ \Rightarrow {P_{Tamil}} = \dfrac{7}{{72}}\]

Converting the above probability in degrees of the pie chart by multiplying it by \[360^\circ \], we get
\[
   \Rightarrow {P_{Tamil}} = \dfrac{7}{{72}} \times 360^\circ \\
   \Rightarrow {P_{Tamil}} = 35^\circ \\
 \]

We will now take language Bengali from the given table.

We will use the formula of probability and substitute the values of the number of outcomes of speaking Bengali and the total number of outcomes, we get
\[
   \Rightarrow {P_{Bengali}} = \dfrac{4}{{72}} \\
   \Rightarrow {P_{Bengali}} = \dfrac{1}{{18}} \\
 \]

Converting the above probability in degrees of the pie chart by multiplying it by \[360^\circ \], we get
\[
   \Rightarrow {P_{Bengali}} = \dfrac{1}{{18}} \times 360^\circ \\
   \Rightarrow {P_{Bengali}} = 20^\circ \\
 \]

Using the above probabilities of languages Hindi, English, Marathi, Tamil and Bengali, we will make the pie chart.

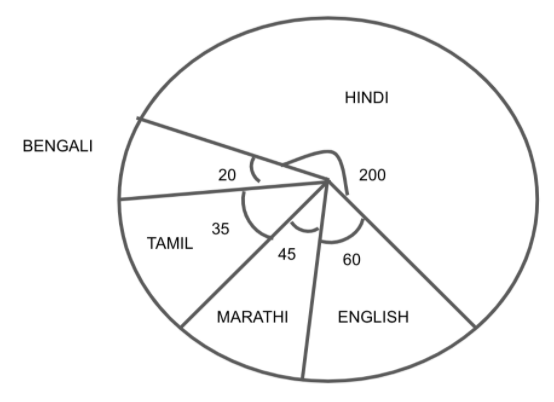
Note: One should know that the probability is simply how likely something is to happen. Students need to convert the probability in degrees of the pie chart by multiplying it by \[360^\circ \], They divide the probabilities by 360 degrees instead of multiplying, which is wrong.