Question

The number of integers n for which $3{x^3} - 25x + n = 0$ has three real roots is?
$\left( a \right)$ 1
$\left( b \right)$ 25
$\left( c \right)$ 55
$\left( d \right)$ Infinite

Answer 1

Hint: In this particular question use the concept that between two roots of derivative, a function has at least 1 root, so differentiate the given function and equate to zero and solve for x, then on these value of x calculate the value of function f (x), so use these concepts to reach the solution of the question.

Complete step-by-step solution:
Given equation:
$3{x^3} - 25x + n = 0$
As we see that the highest power of x is 3, so it is a cubic equation.
Let, $f\left( x \right) = 3{x^3} - 25x + n$
Now as we all know that between two roots of derivative, a function has at least 1 root.
To differentiate the given function and equate it to zero and solve for x, then on these values of x calculate the value of function f (x).
Now differentiate f (x) we have,
$ \Rightarrow \dfrac{d}{{dx}}f\left( x \right) = \dfrac{d}{{dx}}\left( {3{x^3} - 25x + n} \right)$
Now as we know that, \[\dfrac{d}{{dx}}{x^n} = n{x^{n - 1}}\] so use this property in the above equation we have,
$ \Rightarrow \dfrac{d}{{dx}}f\left( x \right) = f'\left( x \right) = 3\left( 3 \right){x^{3 - 1}} - 25 + 0$
$ \Rightarrow f'\left( x \right) = 9{x^2} - 25$
Now equate this to zero we have,
$ \Rightarrow 9{x^2} - 25 = 0$
$ \Rightarrow 9{x^2} = 25$
$ \Rightarrow {x^2} = \dfrac{{25}}{9}$
Now take square root on both sides we have,
$ \Rightarrow x = \sqrt {\dfrac{{25}}{9}} = \pm \dfrac{5}{3}$
Now double differentiate the function to check at which value function attains maxima or minima.
$ \Rightarrow \dfrac{{{d^2}}}{{d{x^2}}}f\left( x \right) = f''\left( x \right) = \dfrac{d}{{dx}}f'\left( x \right) = \dfrac{d}{{dx}}\left( {9{x^2} - 25} \right) = 18x$
So when, $x = \dfrac{5}{3}$
\[ \Rightarrow f''\left( {\dfrac{5}{3}} \right) = 18\left( {\dfrac{5}{3}} \right) = + 30\] (Positive so it is minima)
And when, $x = - \dfrac{5}{3}$
\[ \Rightarrow f''\left( { - \dfrac{5}{3}} \right) = 18\left( { - \dfrac{5}{3}} \right) = - 30\] (Negative so it is maxima)
So the value of f (x) at these roots we have,
So when, $x = \dfrac{5}{3}$
$ \Rightarrow f\left( {\dfrac{5}{3}} \right) = 3{\left( {\dfrac{5}{3}} \right)^3} - 25\left( {\dfrac{5}{3}} \right) + n$
$ \Rightarrow f\left( {\dfrac{5}{3}} \right) = \dfrac{{125}}{9} - \dfrac{{125}}{3} + n$
$ \Rightarrow f\left( {\dfrac{5}{3}} \right) = - \dfrac{{250}}{9} + n$ (Minimum value)
And when, $x = - \dfrac{5}{3}$
$ \Rightarrow f\left( { - \dfrac{5}{3}} \right) = 3{\left( { - \dfrac{5}{3}} \right)^3} - 25\left( { - \dfrac{5}{3}} \right) + n$
$ \Rightarrow f\left( { - \dfrac{5}{3}} \right) = - \dfrac{{125}}{9} + \dfrac{{125}}{3} + n$
$ \Rightarrow f\left( { - \dfrac{5}{3}} \right) = \dfrac{{250}}{9} + n$ (Maximum value)

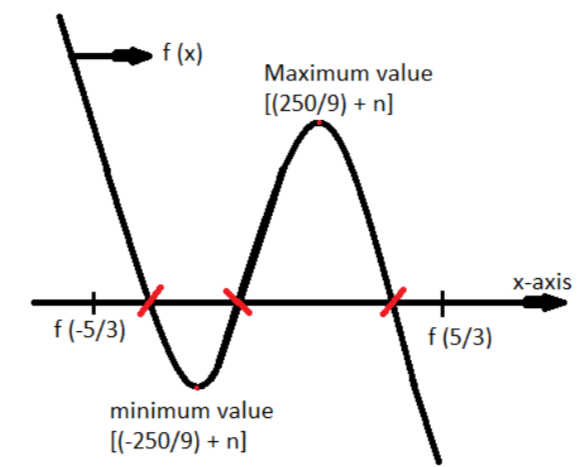
Now for the cubic equation to have three real roots $f\left( {\dfrac{{ - 5}}{3}} \right) > 0$ and $f\left( {\dfrac{5}{3}} \right) < 0$ as shown in the above figure.
Therefore, $f\left( { - \dfrac{5}{3}} \right) > 0 \Rightarrow \dfrac{{250}}{9} + n > 0$
$ \Rightarrow n > \dfrac{{ - 250}}{9}$
And
$f\left( {\dfrac{5}{3}} \right) < 0 \Rightarrow - \dfrac{{250}}{9} + n < 0$
$ \Rightarrow n < \dfrac{{250}}{9}$
Therefore,
$ - \dfrac{{250}}{9} < n < \dfrac{{250}}{9}$
$ \Rightarrow - 27.77 < n < 27.77$
Now we have to find out the integers value of n.
$ \Rightarrow n \in \left[ { - 27,27} \right]$ (I.e. closed interval from -27 to 27).
And the number of integer values from -27 to 27 is 55.
So there are 55 integers’ values of n for which the given cubic equation has 3 real roots.
So this is the required answer.
Hence option (C) is the correct answer.

Note: Whenever we face such types of questions the key concept we have to remember is that always recall that if a function crosses the x-axis then there is the real root of the function, so if a function crosses n times the x-axis then there are n real roots of the function, and always recall the basic differentiation property which is stated above.