Question

The minimum energy required to overcome the attractive forces between an electron and the surface of $Ag$ metal is $552 \times {10^{ - 19}}J$. What will be the maximum kinetic energy of electron ejected out from $Ag$ which is being exposed to UV light of $\lambda = 360A^\circ $

Answer 1

Hint: When an electron attempts to escape from a metal surface it leaves a positive picture behind on the metal surface. The negative electron switches back to the metal surface due to the attractiveness of this positive image, so it does not permanently leave the metal crystal. But an electron requires adequate energy supplied from outside, typically from external light sources, to overcome the attraction factor. The total energy absorbed by the electron will be the net amount of both energy required to overcome the attractive forces and kinetic energy of the electron.
Formula used:
$E = \dfrac{{hC}}{\lambda }$ where,
$E = $energy absorbed from the light
$h = 6.626 \times {10^{ - 34}}Js$ which is planck's constant
$C = 3 \times {10^8}m/s$ which is the velocity of light

Complete step by step answer:
The given values are,
Energy required to overcome the attractive force $({E_1}) = 552 \times {10^{ - 19}}J$
The wavelength of light $\lambda = 360A^\circ $ which is equal to $360 \times {10^{ - 10}}m$
By Substituting the values in equation $E = \dfrac{{hC}}{\lambda }$
$E = \dfrac{{6.626 \times {{10}^{ - 34}}J \times 3 \times {{10}^8}m/s}}{{360 \times {{10}^{ - 10}}m}}$
$ = 5.522 \times {10^{ - 18}}J$
We know that here $E$ is the ${E_{total}}$ which is the sum of both energy to overcome attractive forces $({E_1})$ and kinetic energy of electrons $({E_k})$
So ${E_{total}} = {E_1} + {E_k}$
Therefore, ${E_k} = {E_{total}} - {E_1}$
$ = (5.52 \times {10^{ - 18}}) - (552 \times {10^{ - 19}})$
$ = - 4.968 \times {10^{ - 17}}J$
This is the required maximum kinetic energy of an electron.


Additional information:
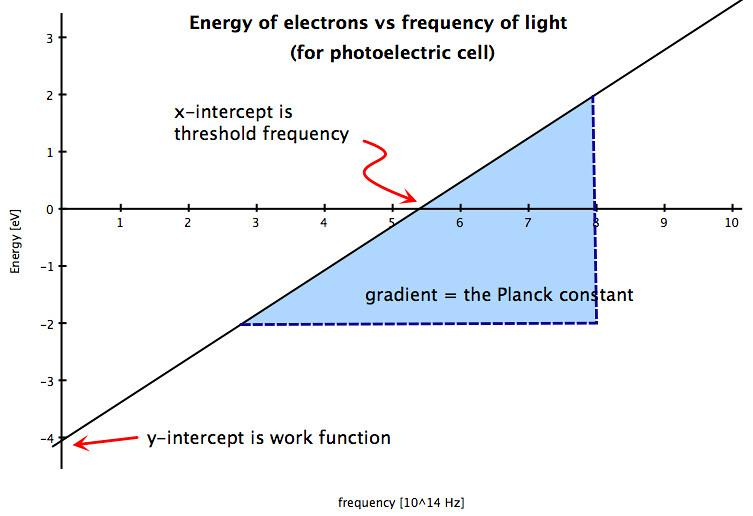
The minimum energy for an electron to overcome the attractive forces and to escape from the metal surface by the striking of a photon is called its work function and is denoted by the symbol $\phi $.The minimum frequency for this emission is called threshold frequency. Energy in always directly proportional to frequency
$E = h\nu $ where $E$ is the energy , $h$ is the planck's constant and $\nu $ is the frequency. The relation is shown by the following graph.

Note:
The energy to overcome the surface is given in $J$, so while doing the calculations take Planck's constant value also in joule. And wavelengths should need to convert into meters since we are taking the value of velocity of light in $m/s$.